Dice Loss for Data-imbalanced NLP Tasks
Dice Loss for Data-imbalanced NLP Tasks
许多自然语言处理任务,如序列标注和机器阅读理解(MRC),都面临着严重的数据失衡问题:
- 负样本明显多于正样本,占据绝大多数的负例会支配模型的训练过程,导致模型倾向于负例,而测试时使用的F1指标需要每个类都能准确预测;
- 大量简单负例(easy-negative)使训练不堪重负。负例占绝大多数也意味着其中包含了很多简单样本,这些简单样本对于模型学习困难样本几乎没有帮助,反而会在交叉熵的作用下推动模型遗忘对困难样本的知识。
loss中最常用的交叉熵实际上是以精度为导向的,这造成了训练和测试之间的差异。在训练时,每个训练样本对目标函数的贡献相等,而在测试时,F1 score更关注正例。
本文认为这种问题是交叉熵本身的特点带来的:交叉熵“平等”地看待每一个样本,无论正负,都尽力把它们推向1(正例)或0(负例)。但实际上,对分类而言,将一个样本分类为负只需要它的概率<0.5即可,完全没有必要将它推向0。
基于这个观察,作者使用现有的Dice Loss,并提出一个基于Dice Loss的自适应损失——DSC,在训练时推动模型更加关注困难的样本,降低简单负例的学习度,从而在整体上提高基于F1值的效果。
从Cross Entropy 到 Dice Losses
交叉熵损失(CE)
以二分类作为说明,记输入为 $x$, 输出为一个二值概率 $p = [p_0,p_1]$, 并且有一个二元真值 $y = [y_0,y_1]$
首先交叉熵损失是:
显然,对每个样本,CE都对它们一视同仁,不管当前样本是简单还是复杂。当简单样本有很多时,模型训练就会被这些简单的样本占据,使得模型难以从复杂样本中学习。于是,一种简单的改进方法是,降低模型在简单样本上的学习速率,从而得到下述加权交叉损失:
对不同样本,我们可以设置不同的权重,从而控制模型在该样本上学习的程度。但是此时,权重的选择又变得比较困难。因为我们的目标是缓解数据集的不平衡问题,从而提高基于F1评测标准的效果,我们希望有一种损失函数能够直接作用于F1。
Sørensen–Dice系数(DSC)
一种现有的方法——Sørensen–Dice系数(简称DSC)——去衡量F1。
DSC是一种用于衡量两个集合之间相似度的指标:
如果我们令A是所有模型预测为正的样本的集合,令B是所有实际上为正的样本集合,那么DSC就可以重写为:
其中D数据集,f是一个分类模型。于是在这个意义上DSC与F1是等价的。
既然如此,就直接优化DSC,然而上述表达式是离散的,为此,需要把上述DSC表达式转化为连续的版本,从而可以视作一种soft F1。
对于单个样本x,直接定义它的DSC:
可以看到如果x是父类,那么它的DSC就为0,从而不会对训练有贡献。为了让父类也能有所贡献,所以增加一个平滑项:
但这样一来,又需要我们根据不同的数据集手动地调整平滑项。而且当easy-negative样本很多的时候,即便使用上述平滑项,整个模型训练过程仍然会被它们主导。基于此,我们使用一种“自调节”的DSC(这里就和focal loss很像):
比较上面两个DSC,可以发现,$1-p_1$ 实际上充当了缩放系数,对于简单样本($p_1$ 趋向于1或0),$(1-p_1)p_1$ 使得模型更少地去关注他们。
从导数上看,一旦模型正确分类当前样本(刚刚经过0.5),DSC就会使模型更少关注它,而不是像交叉熵那样,鼓励模型迫近0或1这两个点。这就能有效避免因简单样本过多导致模型训练受到简单样本的支配。
事实上,这比较类似Focal Loss(FL),降低已分好类的样本的学习权重:
不过,FL即使能对简单样本降低学习权重,但它本质上仍然是在鼓励简单样本趋向于0或1,这就和DSC有了本质上的区别。因此,说DSC通过“平衡”简单样本和困难样本的学习过程,从而提高了最终的F1值(因为F1要求各类都有比较好的结果)
Dice Loss(DL)与Tversky Loss(TL)
除了上述DSC外,还比较了两种$DSC_s(x,f)$的变体,分别是Dice Loss(DL)和Tversky Loss(TL):
在$\alpha=\beta=0.5$时,TL就退化为DSC。
损失总结
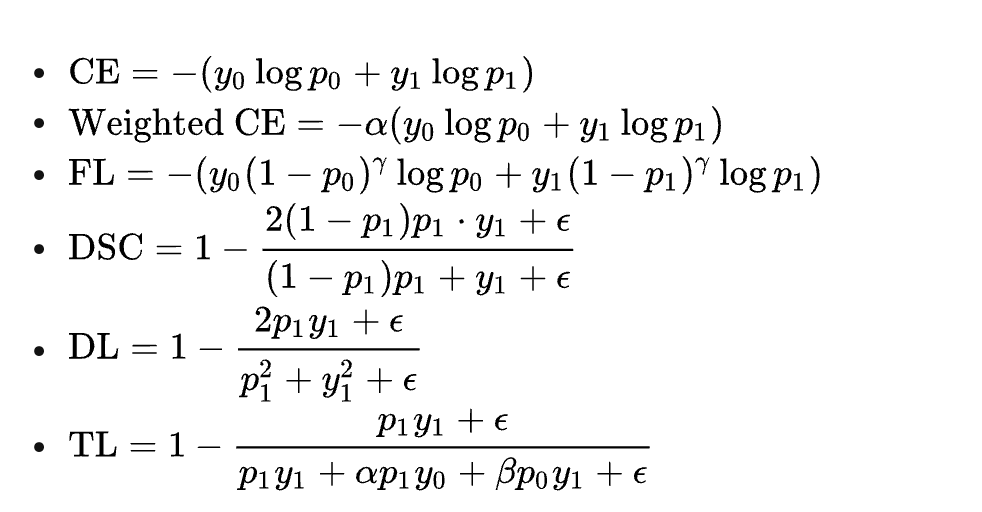
后三个统称为Dice loss







