[TOC]

Continual Learning with Hypernetworks

当人工神经网络在多个任务上进行顺序训练时，它们会遭受灾难性的遗忘。 为了克服这个问题，我们提出了一种基于任务条件超网络的新方法，即基于任务身份生成目标模型权重的网络。

由于一个简单的关键特征，此类模型的持续学习 (CL) 难度较小：任务条件超网络不需要回忆所有先前看到的数据的输入-输出关系，只需要排练特定于任务的权重实现，这可以 使用简单的正则化器在内存中维护。

除了在标准的CL基准上取得最先进的性能外，对长任务序列的额外实验显示，任务条件下的超网络显示出非常大的能力来保留以前的记忆。

值得注意的是，当可训练的超网络权重数量与目标网络大小相当或小于目标网络大小时，如此长的记忆寿命是在一个压缩制度下实现的。我们对低维任务嵌入空间（超网络的输入空间）的结构进行了深入研究，并表明任务条件下的超网络展示了迁移学习。最后，基于CIFAR-10/100图像数据集的挑战性CL基准的经验结果进一步支持了前向信息迁移。

INTRODUCTION

我们假设一个具有可训练权重 $Θ$ 的神经网络 $f(x,Θ)$ 被赋予来自一组任务的数据 ${(X^{(1)}Y^{(1)})}$， 输入样本 $X^{(t)} = {x^{(t,i)}}{i=1}^{n_i}$，输出样本 $Y^{(t)} = {y^{(t,i)}}{i=1}^{n_t}$ , 其中 $n_t = |X^{(t)}|$ 。

一个标准的训练方法是使用所有任务的数据来学习模型 一次性从所有任务中学习模型。然而，这在现实世界的问题中并不总是可能的，在在线学习环境中也不可取。持续学习（CL）指的是一种在线学习设置，其中任务是按顺序呈现的（关于持续学习的最新评论，见van de Ven & Tolias, 2019）。

在CL中，当学习一个新的任务 $t$ 时，从权重 $Θ^{(t-1)}$ 开始，只观察$(X^{(t)},Y^{(t)})$ ，目标是找到一组新的参数 $Θ^{(t)}$，与 $Θ^{( t-1)}$相比，（1）保留（无灾难性遗忘）或（2）提高（正向转移）以前任务的性能，（3）解决新任务 $t$ 可能利用以前获得的知识（正向转移）。实现这些目标是不容易的，也是神经网络研究中的一个长期问题。

在这里，我们提议在 meta level 上解决灾难性遗忘问题：我们不直接尝试为以前的任务保留 $f( x,Θ)$，而是固定一个元模型 $f_h(e,Θ_h)$ 的输出，该模型被称为任务条件超网络，将任务嵌入 $e$ 映射到权重 $Θ$ 。现在，每个任务必须记住single point。

为了激励这种方法，我们做了一个思想实验：我们假设允许我们存储所有的输入 ${X^{(1)},…, X^{(T)} }$，并使用这些数据来计算对应于 $Θ^{(T-1)}$的模型输出。

在这个理想化的设置中，我们可以通过简单地将当前任务的数据与过去的数据混合来避免遗忘，${(X^{(1)}, Y^{(1)}), . . . , (X^{(T -1)}, Y^{(T -1)}), (X^{(T )}, Y^{(T )})}$，其中 $Y^{(t)}$ 是指使用模型本身 $f(-,Θ^{(t-1)})$ 生成的一组合成目标。因此，通过训练保留以前获得的输入-输出映射，我们可以得到一个原则上与多任务学习一样强大的顺序算法。多任务学习，即所有的任务都是同时学习的，可以被看作是CL的上限。上面描述的策略被称为排练（Robins, 1995）。然而，存储以前的任务数据违反了我们的CL要求。

因此，我们引入了一个视角的变化，从维护单个输入输出数据点的挑战转向维护参数集 ${Θ^{(t)}} $ 的问题，而不明确存储它们。
为了实现这一点，我们训练元模型参数 $Θ_h$，类似于上面概述的学习方案，现在的合成目标对应于适合以前任务的权重配置。这样就可以用一个低维任务描述符来交换整个数据集的存储，除了最简单的任务外，还能节省大量内存。尽管依赖于正则化，但我们的方法在概念上与之前基于权重正则化的算法（如Kirkpatrick等人，2017；Zenke等人，2017）或激活空间（如He & Jaeger，2018）有所不同。

我们的实验结果表明，在一组标准的CL基准上，任务条件的超网络并没有遭受灾难性的遗忘。值得注意的是，在面对非常长的任务序列时，它们能够保留记忆，而且性能几乎没有下降。由于神经网络的表达能力，任务条件超网络利用了任务与任务之间的相似性，并将信息及时迁移到未来的任务中。最后，我们提出的任务条件元模型观点是通用的，因为它不依赖于目标网络架构的具体细节。我们利用这一关键原则，并表明同样的元模型框架延伸到并可以改善一类重要的CL方法，即生成性重放方法，这些方法在许多实际问题中是目前最先进的表现（Shin等人，2017；Wu等人，2018；van de Ven & Tolias，2018）。

MODEL

TASK-CONDITIONED HYPERNETWORKS

Hypernetworks parameterize target models. 我们持续学习方法的核心是超网络，图1a。我们不是直接学习一个特定函数 $f{trgt} $ 的参数 $Θ{trgt}$（目标模型），而是学习一个元模型的参数 $Θh$。这种元模型的输出，即超网络，是 $Θ{trgt}$。因此，超网络可以被认为是权重生成器，它最初是为了以压缩的形式动态地对模型进行参数化（Ha等人，2017；Schmidhuber，1992；Bertinetto等人，2016；Jia等人，2016）。

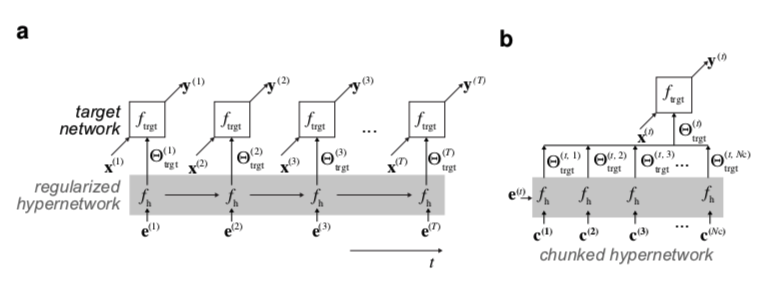
(a) 通常，神经网络的参数是根据数据直接调整的，以解决一个任务。在这里，一个被称为超网络的权重生成器被学习。超网络将嵌入向量映射为权重，从而为目标神经网络提供参数。在持续学习的情况下，一组特定任务的嵌入是通过反向传播学习的。嵌入向量提供与任务相关的背景，并使超网络偏向于特定的解决方案。

(b) 一个较小的、分块的超网络可以被反复使用，一次产生一大块目标网络权重（例如，一次一个层）。分块超网络可以实现模型压缩：可训练参数的有效数量可以小于目标网络权重的数量。

Continual learning with hypernetwork output regularization. 避免灾难性遗忘的一种方法是存储以前任务的数据和相应的模型输出，然后固定这种输出。这可以通过以下形式的输出正则器来实现，其中过去的输出起到了伪目标的作用（Robins, 1995; Li & Hoiem, 2018; Benjamin等人, 2018）

$$L_{output} = \sum_{t=1}^{T-1} \sum_{i=1}^{|X^{(t)}|} ||f(x^{(t,i)}, \theta^*) - f(x^{(t,i)}, \theta)||^2$$

在上面的方程式中，$Θ^∗$是尝试学习任务 $T$ 之前的参数集，$f$ 是学习者。然而，这种方法需要存储和迭代以前的数据，这个过程被称为排练。这在内存方面可能很昂贵，而且不是严格意义上的在线学习。一个可能的变通方法是通过对随机模式（Robins, 1995）或当前任务数据集（Li & Hoiem, 2018）评估 $f$ 来生成伪目标。然而，这不一定能固定函数 $f$ 在感兴趣区域的行为。

超网络自然避开了这个问题。在目标网络权重空间中，每个任务必须固定一个点（即一组权重）。这可以通过任务条件超网络有效地实现，即把超网络的输出固定在适当的任务嵌入上。

与Benjamin等人（2018）类似，我们使用两步优化程序来引入内存保护的超网络输出约束。首先，我们计算出一个候选变化 $ΔΘh$，该变化使当前任务损失 $L(T)=L{task}(Θ_h,e^{(T)},X^{(T)},Y^{(T)})$ 相对于 $Θ$ 最小。候选任务 $∆Θ_h$ 是通过选择的优化器得到的（我们自始至终使用Adam；Kingma & Ba, 2015）。然后通过最小化以下总损失来计算实际的参数变化:

$$\begin{equation}\begin{split} L_{total} &= L_{task}(\theta_h, e^{(T)}, X^{(T)}, Y^{(T)}) + L_{output} (\theta_{h}^*, \theta_h, \Delta \theta_{h}, \{e^{t}\})\\ &= L_{task}(\theta_h, e^{(T)}, X^{(T)}, Y^{(T)}) + \frac{\beta_{output}}{T-1} \sum_{t=1}^{T-1}||f_h(e^{(t)}, \theta^*_h) - f_h(e^{(t)}, \theta_h + \Delta\theta_h)||^2 \end{split}\end{equation}$$

其中 $Θ^∗h$ 是尝试学习任务 $T$ 之前的超网络参数集，$ΔΘ_h$ 被认为是固定的，$β{output}$是一个控制正则器强度的超参数。在附录D中，我们对 $β_{output}$进行了敏感性分析，并实验了一个更有效的随机正则器，其中平均化是在过去任务的一个随机子集上进行的。

可以采用更多的计算密集型算法，包括完整的内环细化，或者通过 $∆Θh$的反向传播使用二阶梯度信息。然而，我们根据经验发现，我们的单步校正效果很好。探索性的超参数扫描显示，在加入前瞻 $∆Θ_h$带来了性能上的小幅提升，即使是用廉价的一步程序计算时。请注意，与公式1不同的是，保存记忆的项 $L{output}$并不依赖于过去的数据。以前任务的记忆只通过以下集合进入任务嵌入 ${e^{(t)}}^{T-1}_{t-1}$。

Learned task embeddings. 任务嵌入是可以学习的可区分的确定性参数，就像 $Θh$ 一样。**在我们算法的每个学习步骤中，我们也会更新当前的任务嵌入 $e^{(T )}$，以最小化任务损失 $L^{(T)}{task}$。学习任务后，最终的嵌入被保存下来 并添加到集合${e^{(t)}}$中。**

MODEL COMPRESSION WITH CHUNKED HYPERNETWORKS

Chunking. 在一个直接的实现中，超网络产生目标神经网络的整个权重集。对于现代深度神经网络，这是一个非常高维的输出。然而，超网络可以被迭代调用，在每一步只填入目标模型的一部分，分块进行（Ha等人，2017；Pawlowski等人，2017）。这种策略允许应用可重复使用的较小的超网络。有趣的是，通过分块超网络，有可能在压缩制度下解决任务，其中学习的参数（超网络的参数）的数量实际上小于目标网络参数的数量。

Chunk embeddings and network partitioning. 多次重新应用相同的超网络会在目标网络的各个分区中引入权重共享，这通常是不可取的。为了允许目标网络的灵活参数化，我们引入了一组 $C={ci}^{N_c}{i=1}$ 的块嵌入，它们被用作超网络的额外输入，图1b。因此，整套目标网络参数 $Θ{trgt}=[f_h(e,c_1),…,f_h(e,c{N_C})]$ 是通过对 C 的迭代产生的，保持任务嵌入e不变。这样，超网络可以为每个块产生不同的权重。此外，块嵌入，就像任务嵌入一样，是普通的确定性参数，我们通过反向传播学习。为了简单起见，我们对所有任务使用一组共享的块嵌入，我们不探索特殊的目标网络分区策略。

我们的方法有多灵活？分块神经网络原则上可以任意地接近任何目标权重配置。为了完整起见，我们在附录E中正式说明这一点。

CONTEXT-FREE INFERENCE: UNKNOWN TASK IDENTITY

Determining which task to solve from input data. 我们的超网络需要一个任务嵌入输入来生成目标模型权重。在某些CL应用中，可以立即选择一个合适的嵌入，因为任务身份是明确的，或者可以很容易地从上下文线索中推断出来。在其他情况下，手头的任务知识在推理过程中并不明确可用。在下文中，我们展示了我们的元模型框架对这种情况的概括。特别是，我们考虑从一个给定的输入模式中推断出要解决的任务的问题，这是一个著名的基准挑战（Farquhar & Gal, 2018; van de Ven & Tolias, 2019）。下面，我们探讨了在这种CL设置中利用任务条件超网络的两种不同策略。

Task-dependent predictive uncertainty. 神经网络模型在指示新奇性和适当处理分布外数据方面越来越可靠。对于分类目标分布，网络最好对未见过的数据产生平坦的、高熵的输出，反之，对分布中的数据产生峰值、低熵的响应（Hendrycks & Gimpel, 2016; Liang et al., 2017）。这表明了第一种简单的任务推理方法（HNET+ENT）。给定一个任务身份未知的输入模式，我们选择产生最低预测不确定性的任务嵌入，这是由输出分布熵量化的。虽然这种方法依赖于精确的新奇性检测，而这本身就是一个远未解决的研究问题，但它在其他方面的实现是很简单的，不需要额外的学习或模型来推断任务身份。

Hypernetwork-protected synthetic replay. 当生成模型可用时，灾难性遗忘可以通过将当前任务数据与重放的过去合成数据混合来规避（最近的工作见Shin等人，2017；Wu等人，2018）。除了保护生成模型本身，合成数据还可以保护另一个感兴趣的模型，例如另一个区分性模型。这种概念上简单的策略在实践中往往是最先进的CL解决方案（van de Ven & Tolias, 2019）。受这些成功的启发，我们探索用重放网络来增强我们的系统，这里是一个标准的变异自动编码器（VAE；Kingma & Welling，2014）（但见附录F中的生成对抗网络实验，Goodfellow等人，2014）。

合成重放是一个强大的，但并不完美的CL机制，因为生成模型会出现漂移，而错误往往会随着时间的推移而积累和放大。在此，我们基于以下关键观察：就像目标网络一样，重放模型的生成器可以由超网络指定。这允许用输出正则器（公式2）来保护它，而不是像相关工作中那样，用模型自身的重放数据来保护它。因此，在这个组合方法中，合成重放和任务条件元模型都是串联起来的，以减少遗忘。

我们在两个不同的设置中探索超网络保护的重放。首先，我们考虑一个最小的架构（HNET+R），其中只有重放模型，而不是目标分类器，是由超网络提供参数。在这里，目标网络中的遗忘是通过混合当前数据和合成数据来避免的。以前任务的合成目标输出值是用软目标方法产生的，即在合成输入数据上学习新任务之前简单地评估目标函数。其次（HNET+TIR），我们引入了一个辅助的任务推理分类器，使用合成重放数据进行保护，并训练它从输入模式预测任务身份。这种结构需要额外的建模，但当任务有强烈的不相似性时，它可能会很好地工作。此外，任务推理子系统可以很容易地应用于处理更普遍形式的上下文信息，超越了当前的输入模式。我们在附录B和附录C中提供了更多的细节，包括网络结构和被优化的损失函数。

RESULTS

我们在MNIST、CIFAR-10和CIFAR-100公共数据集的一组标准图像分类基准上评估我们的方法1。我们的主要目的是：（1）研究任务条件超网络在三种持续学习环境中的记忆保持能力，以及（2）研究在连续学习的任务中的信息转移。

Continual learning scenarios.

在我们的实验中，我们考虑了三种不同的CL场景。在CL1中，任务身份被赋予了系统。这可以说是标准的顺序学习情景，除非另有说明，否则我们考虑的就是这种情景。在CL2中，任务身份对系统来说是未知的，但它不需要明确地确定。需要一个有固定头部的目标网络来解决多个任务。在CL3中，任务身份必须被明确推断出来。有人认为，这种情况是最自然的，也是对神经网络来说比较困难的。

Experimental details

为了实现可比性，在MNIST数据集的实验中，我们将目标网络建模为全连接网络，并按照van de Ven & Tolias（2019）的方法设置所有超参数，他们最近审查并比较了一大批CL算法。对于我们的CIFAR实验，我们选择了ResNet-32目标神经网络（He等人，2016）来评估我们方法的可扩展性。附录C提供了对架构和特定超参数选择的简要描述，以及其他实验细节。我们强调，在我们所有的实验中，超网络参数的数量总是小于或等于我们与之比较的模型的参数数量。

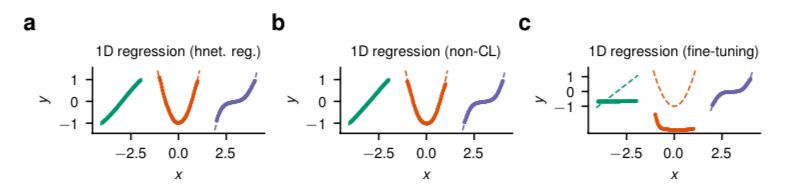
图2：一维非线性回归。(a) 具有输出正则化的任务条件超网络可以很容易地对一连串度数增加的多项式建模，同时以持续的方式学习。(b) 直接对所有任务同时进行训练的目标网络找到的解决方案是相似的。(c) 微调，即按顺序学习，导致对过去任务的遗忘。虚线描述的是基础事实，标记显示的是模型预测。

Nonlinear regression toy problem.

为了说明我们的方法，我们首先考虑一个简单的非线性回归问题，其中要近似的函数是标量值的，图2。在这里，必须从嘈杂的数据中推断出一串度数增加的多项式函数。这激发了持续学习的问题：当通过修改 $Θ_h$并关闭保存记忆的正则器（βoutput = 0，见公式2）来连续学习每个任务时，网络学习了最后的任务，但忘记了以前的任务，图2c。正则器保护了旧的解决方案，图2a，并且性能与离线非连续学习器相当，图2b。

Permuted MNIST benchmark.

接下来，我们研究了permuted MNIST基准。这个问题的设置如下。首先，向学习者提供完整的MNIST数据集。随后，通过对输入的图像像素进行随机置换，获得新的任务。这个过程可以重复进行，以产生一个长的任务序列，其典型长度为T=10个任务。考虑到生成的任务的低相似性，混杂的MNIST很适合研究持续学习者的记忆能力。对于T=10，我们发现，任务条件超网络在CL1上是最先进的，表1。有趣的是，通过预测分布熵（HNET+ENT）推断出的任务在permuted MNIST基准上效果很好。尽管方法简单，但突触智能（SI；Zenke等人，2017）和在线弹性重量巩固（EWC；Schwarz等人，2018）在CL3上的表现都要高出很多。当辅以生成性重放 方法时，任务条件超网络（HNET+TIR和HNET+R）在所有三种CL场景中表现最好。

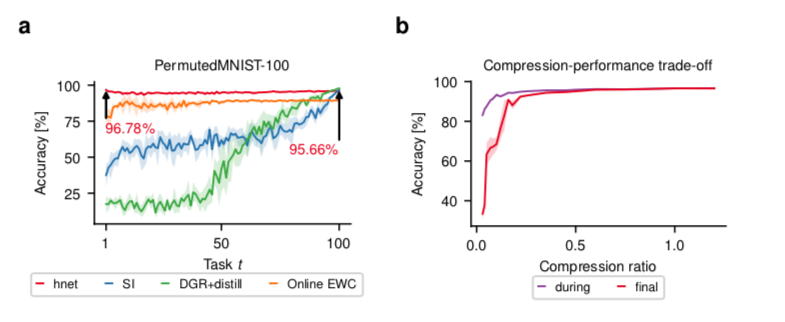
图3：在置换的MNIST基准上进行的实验。(a) 在学习了一百个排列组合（PermutedMNIST-100）之后，第 $t$ 个任务的最终测试集分类准确率。任务条件下的超网络（hnet，红色）在permuted MNIST基准上实现了非常大的记忆寿命。突触智能（SI，蓝色；Zenke等人，2017）、在线EWC（橙色；Schwarz等人，2018）和深度生成重放（DGR+distill，绿色；Shin等人，2017）方法被显示出来进行比较。SI和DGR+distill的记忆保持率优雅地下降，而EWC则受到僵化的影响，永远无法达到非常高的准确性，即使记忆持续了整个实验时间。(B)压缩比 $\frac{|\thetah \cup {e^{(t)}}|}{\theta{trgt}}$对于PermutedMNIST-10基准，在学习所有任务(标记为“最终”，红色)之后和紧接着学习任务(标记为“期间”，紫色)之后的任务平均测试集准确性。超网络允许模型压缩，即使目标模型参数的数量超过其自身，也有良好的表现。性能的衰减是非线性的：在压缩比低于1的大范围内，精度保持大致不变。对压缩比≈1的超参数进行一次调整，然后用于所有压缩比。阴影部分表示5个随机种子的STD（a）和SEM（b）。

在长序列的限制下，性能差异变得更大，图3a。对于较长的任务序列（T=100），SI和DGR+distill（Shin等人，2017；van de Ven & Tolias，2018）优雅地退化，而在线EWC的正则化强度使该方法无法实现高精确度（见图A6，关于相关工作的超参数搜索）。值得注意的是，任务条件的超网络显示出最小的内存衰减，并找到高性能的解决方案。由于超网络在压缩制度下运行（见图3b和图A7对压缩率的探索），我们的结果并不天真地依赖于参数数量的增加。相反，它们表明以前的方法还没有能力在CL环境下充分利用目标模型的能力。我们在附录D中报告了一组关于该基准的扩展结果，包括对CL2/3（T=100）的研究，其中HNET+TIR强烈地超过了相关工作。

Split MNIST benchmark.

拆分MNIST是另一个流行的CL基准，旨在引入任务重叠。在这个问题中，各种数字被依次配对，并用于形成五个二进制分类任务。在这里，我们发现任务条件下的超网络是整体表现最好的。特别是，HNET+R在CL2和CL3上都改进了以前最先进的方法DGR+distill，几乎饱和了重放模型的CL2上限（附录D）。由于HNET+R本质上是超网络保护的DGR，这些结果证明了任务条件超网络作为有效内存保护器的普遍性。为了进一步支持这一点，我们在附录F中表明，我们的重放模型（我们用VAE和GAN做实验）可以以类增量的方式学习完整的MNIST数据集。最后，HNET+ENT再次胜过EWC和SI，没有任何生成模型。

在分裂的MNIST问题上，任务是重叠的，因此持续学习者可以跨任务转移信息。为了分析这种影响，我们研究了具有二维任务嵌入空间的任务条件超网络，它可以很容易地被可视化。尽管学习是持续进行的，但我们 我们发现，在适当的任务嵌入下，算法会收敛到一个超网络配置，该配置可以产生同时解决新旧任务的目标模型参数，图4。

图4：分裂的MNIST基准的二维任务嵌入空间。在学习了五种拆分后的彩色编码的测试集分类准确率，随着嵌入向量成分的变化而显示。标记表示最终任务嵌入的位置。(a) 即使e-空间是低维的，也能实现高分类性能，几乎没有遗忘。该模型显示了嵌入空间中的信息转移：第一个任务在一个包括后续学习任务的嵌入的大体积中得到解决。(b) 嵌入空间的竞争：最后一个任务占据了一个有限的高性能区域，在远离嵌入矢量的地方出现了优雅的退化。以前学到的任务嵌入仍然导致适度的、高于机会的性能。

Split CIFAR-10/100 benchmark

最后，我们研究了一个更具挑战性的基准，学习者首先被要求解决完整的CIFAR-10分类任务，然后从CIFAR-100数据集中拿出10个类别的集合。我们用一个高性能的ResNet-32目标网络结构（图5）和一个较浅的模型（图A3）进行了实验，我们完全复制了以前的工作。值得注意的是，在ResNet-32模型上，我们发现有任务条件的超网络基本上可以完全消除遗忘。此外，还发生了前向信息转移；与从初始条件单独学习每个任务时相比，来自先前任务的知识使网络能够找到更好的解决方案。有趣的是，在浅层模型实验中，前向转移更强（图A3），否则我们发现我们的方法与SI的表现相当。

DISCUSSION

Bayesian accounts of continual learning.

根据标准的贝叶斯CL观点，后验参数分布是使用贝叶斯规则递归更新的，因为任务到达了. 虽然这种方法在理论上是合理的，但在实践中，通常首选的近似推理方法会导致僵硬的模型，因为必须在第一个任务确定的模式内找到适合所有任务的折中方案。 这种限制并不适用于超网络，它原则上可以为复杂的多模态分布建模。因此，丰富的、超网络建模的先验是贝叶斯CL方法的一个改进途径。有趣的是，任务条件提供了另一种可能性：与其把每个任务合并到一个单一的分布上，不如利用一个共享的任务条件超网络来模拟一组参数后验分布。这种条件元模型自然地将我们的框架扩展到贝叶斯学习环境中。与传统的递归贝叶斯更新相比，这种方法可能会受益于额外的灵活性。

Related approaches that rely on task-conditioning.

我们的模型符合，并在某些方面概括了以前的CL方法，该方法将网络计算置于任务描述符上。任务条件通常在模块（Rusu等人，2016；Fernando等人，2017）、神经元（Serra等人，2018；Masse等人，2018）或权重（Mallya和Lazebnik，2018）层面上使用乘法掩码来实现。这类方法在大型网络中效果最好，而且有很大的存储开销，通常随着任务数量的增加而增加。我们的方法与之不同，它使用元模型，即超网络，明确地对全部参数空间进行建模。由于这个元模型，参数和任务空间的泛化是可能的，任务与任务之间的依赖关系可以被利用来有效地表示解决方案，并将目前的知识转移到未来的问题中。有趣的是，与我们同时进行的工作中也得出了类似的论点（Lampinen & McClelland, 2019），在那里，任务嵌入空间在几率学习的背景下被进一步探索。同样，和这里开发的方法一样，最近在CL中的工作将最后一层网络参数作为管道的一部分来生成，以避免灾难性遗忘（Hu等人，2019），或者将参数提炼到一个收缩的自动编码模型上（Camp等人，2018）。

Positive backwards transfer.

在其目前的形式下，超网络输出正则器保护以前学到的解决方案不发生变化，这样就只能发生弱的信息反向转移。鉴于选择性遗忘和完善过去的记忆在实现智能行为方面的作用（Brea等人，2014年；Richards和Frankland，2017年），调查和改进反向转移是未来研究的一个重要方向。

Relevance to systems neuroscience.

揭示支持大脑和人工神经网络持续学习的机制是一个长期存在的问题（McCloskey & Cohen, 1989; French, 1999; Parisi et al., 2019）。最后，我们对我们的工作进行了推测性的系统解释（Kumaran等人，2016；Hassabis等人，2017），作为大脑皮层中自上而下的调制信号的模型。任务嵌入可以被看作是低维语境开关，它决定了一个调节系统的行为，在我们的案例中是超网络。根据我们的模型，超网络将反过来调节目标皮质网络的活动。

就目前而言，实现超网络需要动态地改变目标网络或皮层区域的整个连接。这样的过程在大脑中似乎很难想象。然而，这种严格的字面解释是可以放松的。例如，超网络可以输出低维的调节信号（Marder，2012），而不是一整套的权重。 这种解释与越来越多的工作是一致的，这些工作表明调节性输入参与实施上下文或任务相关的网络模式切换（Mante等人，2013；Jaeger，2014；Stroud等人，2018；Masse等人，2018）。

CONCLUSION

我们引入了一种新的神经网络模型—任务条件超网络，它非常适合于CL问题。任务条件超网络是一个元模型，它可以学习目标函数的参数化，这些目标函数是用任务嵌入向量以压缩的形式指定和识别的。过去的任务使用超网络输出正则器保存在内存中，该正则器对以前发现的目标权重配置的变化进行惩罚。这种方法是可扩展的和通用的，可作为独立的CL方法或与生成性重放结合使用。我们的结果在标准基准上是最先进的，并表明任务条件下的超网络可以实现较长的记忆寿命，以及将信息转移到未来的任务中，这是持续学习者的两个基本属性。

TASK-CONDITIONED HYPERNETWORKS: MODEL SUMMARY

在我们的模型中，一个有任务条件的超网络产生一个目标神经网络的参数 $Θ{trgt} = f{trgt} (e, Θ{trgt} )$。给定一个这样的参数化，目标模型然后根据输入数据计算预测值 $\hat y=f{trgt}(x,Θ{trgt})$。学习相当于调整超网络的参数 $Θ_h$。超网络的参数，包括一组任务嵌入 ${e^{(t)}}^T{t=1}$，以及一组分块嵌入 ${ci}^{N_C}{i=1}$，以便在寻求压缩或整个超网络太大而无法直接处理的情况下。为了避免灾难性的遗忘，我们引入了一个输出正则器，它通过惩罚目标模型参数的变化来固定超网络的行为，这些变化是针对以前学习的任务而产生的。

Variables that need to be stored while learning new tasks.

在持续学习时，我们的模型的存储要求是什么？

• 内存保留依赖于每个任务保存一个嵌入。因此，这个集合 ${e^{(t)}}^T_{t=1}$随T线性增长。这种线性扩展在渐进上是不可取的，但它在实践中基本上可以忽略不计，因为每个嵌入是一个单一的低维向量（例如，见图4中的2D嵌入运行）。
• 在学习一个新任务之前，需要保留超网络参数 $Θ^∗_h$的冻结快照，以评估公式2中的输出正则器。

ADDITIONAL DETAILS ON HYPERNETWORK-PROTECTED REPLAY MODELS

Variational autoencoders.

对于正文中报告的所有HNET+TIR和HNET+R实验，我们使用VAE作为我们的重放模型（图A1a，Kingma & Welling，2014）。简而言之，VAE由一对编码器-解码器网络组成，其中编码器网络处理一些输入模式 $x$，其输出 $f{enc}(x) = (μ, σ^2)$ 包括一个对角多变量高斯 $p_Z (z; μ, σ^2)$的参数 $μ$ 和 $σ^2$（在对数域中编码，以强制执行非负性），它支配着潜在样本 $z$ 的分布。在电路的另一端，解码器网络处理一个潜伏样本 $z$ 和一个one-hot编码的任务身份向量，并返回一个输入模式重建，$f{dec}（z，1_t）=\hat x$。

VAEs可以使用一种叫做生成性重放的技术来保存记忆：当训练任务$T$时，通过改变 $1_t$ 和抽取潜伏空间样本 $z$，从当前重放网络中生成旧任务 $t<T$ 的输入样本。生成的数据可以与当前数据集混合，产生一个增强的数据集 $\gat X$，用于重新学习模型参数。当保护一个判别性模型时，可以通过在 $\hat X$上评估网络来生成合成的 “软 “目标。我们使用这种策略来保护HNET+TIR中的辅助任务推理分类器，并保护HNET+R中的主要目标模型。

Hypernetwork-protected replay.

在我们的HNET+TIR和HNET+R实验中，我们通过任务条件超网络 $f{h,dec}(e,Θ{h,dec})$ 对解码器网络进行参数化。与我们的输出正则器相结合，这使我们能够利用超网络的记忆保留能力，现在是在生成模型上。

重放模型（编码器、解码器和解码器超网络）是一个独立的子系统，独立于目标网络进行优化。它的参数 $Θ{enc}$和$Θ{h,dec}$是通过最小化我们的正则化损失函数（公式2）来学习的，这里的任务特定项被设置为标准的VAE目标函数：

$$L_{VAE}(X,\theta_{enc},\theta_{h,dec}) = L_{rec}(X,\theta_{enc},\theta_{dec}) + L_{prior}(X,\theta_{enc},\theta_{dec})$$

$Θ{dec} = f{h,dec}(e, Θ{h,dec})$引入对 $Θ{h,dec}$的依赖。$L{VAE}$平衡了一个重建 $L{rec}$和一个先验匹配 $L_{prior}$的惩罚。对于我们的MNIST实验，我们选择二进制交叉熵（在像素空间）作为重建损失，我们在下面写出一个单一的例子 x

$$L_{rec} (x,\theta_{enc},\theta_{dec}) = L_{xent}(x,f_{dec}(z, 1_{t(x)}, \theta_{dec}))$$

其中$L{xent}(t,y) = - \sum{k}t_klogy_k$是交叉熵，对于一个对于对角线高斯 $p_Z$，先验匹配项可以用分析法评估:

$$L_{prior} = -\frac{1}{2}\sum_{i=1}^{|z|}(1+log\sigma^2_i-\sigma_i^2-\mu_i^2)$$

以上，$z$ 是通过重新参数化技巧获得的 $pZ（z;μ(\hat x),σ^2(\hat x))$的样本（Kingma & Welling，2014；Rezende等人，2014）。这就引入了 $L{rec}$对 $Θ_{enc}$的依赖性。

Task inference network (HNET+TIR).

在HNET+TIR设置中，我们将我们的系统扩展到包括一个任务推理神经网络分类器 $α(x)$，参数为 $Θ_{TI}$，其中任务被编码为一个T-维softmax输出层。在CL2和CL3场景中，我们对 $α$ 使用了一个不断增长的单头设置，并随着任务的到来增加softmax层的维度。

当任务不断被学习时，这个网络很容易出现灾难性的遗忘。为了防止这种情况的发生，我们借助于上述由超网络保护的VAE产生的重放数据。更具体地说，我们引入了一个任务推理损失。

$$L_{TI} (\hat x,\theta_{TI}) = L_{xent} (1_{t(\hat x)}, \alpha(\hat x,\theta_{enc}))$$

其中 $t(\hat x)$表示从增强的数据集 $\hat X= {\hat X^{(1)},…,\hat X^{(T-1)},\hat X^{(t)}}$, 其中 $\hat X^{(t)}$ 是 $t=1…T-1$ 的合成数据$fdec(z,1_t,Θ{dec})$，而 $\hat X^{(T)}= X^{(T )}$是当前任务数据。重要的是，合成数据对于获得任务推理的定义明确的目标函数至关重要；交叉熵损失$L_{TI}$至少需要两个groundtruth类来进行优化。请注意，重放的数据可以通过从先验中抽取样本 $z$ 来在线生成。

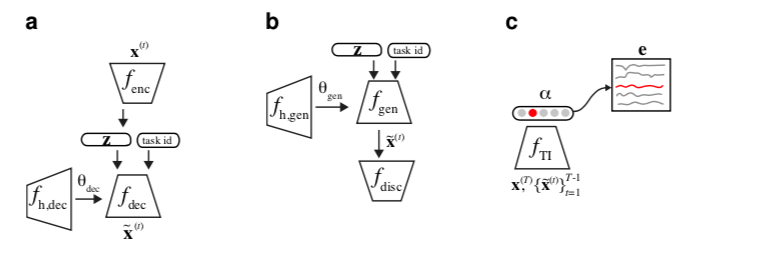
图A1：超网络保护的重放模型设置。(a) 一个超网络保护的VAE，我们用于HNET+R和HNET+TIR正文实验。(b) 一个超网络保护的GAN，我们用于类增量学习附录F的实验。(c) 一个用合成重放数据保护的任务推理分类器，用于HNET+TIR的实验。

Hypernetwork-protected GANs

生成对抗网络（Goodfellow等人，2014年）已经成为生成建模的既定方法，与VAE相比，往往能产生更高质量的图像，即使是在ImageNet这样复杂的数据集规模下（Brock等人，2019年；Lucˇić等人，2019年；Donahue & Simonyan，2019年）。这使得GAN成为强大重放模型的完美候选者。Wu等人（2018）研究的条件GAN（Mirza & Osindero，2014）是CL的一个合适的GAN实例。GAN文献的最新发展已经暗示了使用类似超网络结构的潜力，例如，在注入潜伏噪声时（Karras等人，2019年）或使用类条件批量规范化时，如（Brock等人，2019年）。我们建议更进一步，使用一个超网络，将条件映射到生成器参数的完整集合 $Θ^∗_{gen}$。我们的框架允许一次训练一个条件性的GAN。这可能具有普遍意义，并超出了重放模型的范围，因为像Brock等人（2019）那样以多任务方式训练的条件GAN需要非常大的计算资源。

对于我们关于类增量MNIST学习的展示实验，图A8，我们的目的不是与相关工作进行比较，因此没有调整超网络中的权重比目标网络中的权重少（对于VAE实验，我们使用与正文中相同的压缩设置，见附录C）。GAN超网络是一个全连接的分块超网络，有2个大小为25和25的隐藏层，然后是75000的输出大小。我们对鉴别器和生成器超网络的学习率都是0.0001，鉴别器的辍学率也是0.4，系统对每个任务进行了10000次迭代训练。我们在实验中使用Mao等人（2017）的Pearson Chi2 Least-Squares GAN损失。

ADDITIONAL EXPERIMENTAL DETAILS

所有的实验都是使用16个NVIDIA GeForce RTX 2080 TI显卡进行的。

为了简单起见，我们决定始终保持以前的任务嵌入 $e^{(t)}$ , $t = 1, . . . , T - 1$，固定不变，只学习当前的任务嵌入 $e^{(T)}$。一般来说，如果公式2中的正则器有一份学习当前任务之前的任务嵌入 $e^{(t,∗)}$的单独副本，这样 $e^{(t)}$就可以被适应，性能就应该得到提高。因此，目标成为 $f_h(e^{(t,∗)},Θ^∗_h)$ 并保持不变。同时学习任务T。这将使超网络具有调整嵌入的灵活性，即目标的预像，因此代表了任何包括其图像中所有期望目标的函数。

HNET+TIR的VAE的细节。对于这个变异自动编码器，我们使用两个全连接的神经网络，编码器的层数为1000，1000，解码器为1000，潜伏空间为100。这个设置也是从我们比较的工作中复制过来的。

HNET+R的VAE的细节。对于这个变异自动编码器，我们使用两个全连接的神经网络，编码器的层数为400，400，解码器的层数为400，400（在相关工作中都是1000，1000），潜空间的维度为100。这里，我们与相关工作不同，为自动编码器选择了一个较小的架构。请注意，我们仍然使用一个超网络，其可训练的参数比相关工作中使用的目标网络（在这种情况下是解码器）少。

PermutedMNIST-10中目标分类器的超网络细节（HNET+TIR & HNET+ENT）。我们使用与上述VAE相同的超网络设置，但由于目标网络较小，我们将超网络的输出减少到78,000。我们还将参数βoutput调整为0.01，与我们的PermutedMNIST-100实验一致。因此，这个超网络的权重数量是2,029,931个参数（2,029,691个网络权重+240个任务嵌入权重）。相应的目标网络（来自相关工作）将有2,126,100个权重用于CL1和CL3，2,036,010用于CL2（只有一个输出头）。

PermutedMNIST-100的目标分类器的超网络细节。在这些实验中，我们选择了一个在PermutedMNIST-10基准上运行良好的架构，没有再进行新架构的搜索。对于PermutedMNIST-100，报告的结果是通过使用一个分块超网络获得的，该网络有3个隐藏层，大小为200、250和350（CL2为300），输出大小为7500（CL2为6000）（这样，我们大约与CL1/CL2/CL3的相应目标网络大小一致）。有趣的是，图A2b显示，即使我们不根据目标网络权重的增加来调整超网络权重的数量，我们方法的优越性也是显而易见的。除此之外，图3中的图是用PermutedMNIST-10 HNET+TIR设置生成的（注意，这包括相关工作为PermutedMNIST-10设定的条件，如目标网络大小、训练迭代次数、学习率等）。

PermutedMNIST-100中用于CL2/CL3的VAE和超网络的细节。我们对VAE和它在HNET+TIR中用于PermutedMNIST-10的超网络使用了非常类似的设置，如上所述。我们只做了以下改动。全连接超网络有一个大小为100的隐藏层；块嵌入大小被设置为12；任务嵌入大小被设置为两个128，VAE的隐藏层大小为400，600。同时，我们增加了VAE其生成器超网络的正则化强度βoutput=0.1。

HNET+TIR和HNET+ENT的目标分类器的细节。对于这个分类器，我们使用与我们比较的研究（van de Ven & Tolias, 2019）相同的设置，即一个全连接的网络，层的大小为1000，1000。请注意，如果该分类器被用作任务推理模型，它是在重放数据和相应的硬目标，即软目标的argmax上训练的。

Continual Model-Based Reinforcement Learning with Hypernetworks

使用超网络的任务意识持续学习是一种有效和实用的方法，可以适应新的任务和不断变化的动态，用于基于模型的强化学习，而不需要保留旧任务的状态转换，也不需要向动态模型增加容量。

Hypernetworks for Continual Learning.

超网络[35], [36]是一个生成另一个神经网络的权重的网络。具有权重 $Θ$ 的超网络 $HΘ(e)=θ$ 可以以嵌入向量 $e$ 为条件，通过改变嵌入向量 $e$ 来输出主（目标）网络的权重 $θ$ ，$fθ(x) = f(x; θ) = f(x; H_Θ(e))$。

与主网络相比，超网络的可训练参数数量通常更大，因为超网络中输出层的大小等于目标网络中权重的数量。

超网络已被证明在持续学习环境下[1]对分类和生成模型很有用。这已被证明可以缓解一些灾难性遗忘的问题。它们也被用来实现基于梯度的超参数优化[37]。

我们考虑MBRL的求解设置，它有一个学习的动力学模型，其参数是通过一个任务条件超网络推断出来的。考虑到学习到的任务嵌入 $et$ 和超网络 $H(-)$ 的参数 $Θ_t$，我们推断出动态神经网络 $f{θ_t}(-)$的参数 $θ_t$。利用这个动力学模型，我们进行CEM优化，生成动作序列，并在环境中用MPC执行K个时间步长。我们将观察到的过渡存储在重放数据集中，并更新超网络的参数 $Θ_t$ 和任务嵌入等（非政策性优化）。我们对每个任务的 $M$ 个插曲，以及每 $T$ 个任务的顺序重复这一过程。

动态学习。学习的动力学模型是一个前馈神经网络，其参数在不同的任务中是不同的。在不同的任务中学习动力学网络$fθ(-)$的一种方法是随着训练的进行按顺序更新它。然而，由于我们的问题设置是不允许代理人在重放缓冲器中保留以前任务的状态转换数据，因此在不同任务中按顺序调整单个网络的权重可能会导致灾难性的遗忘[1]。为了减轻灾难性遗忘的问题，**同时试图适应网络的权重，我们学习一个超网络，将任务嵌入作为输入，并输出每个任务对应的动态网络的参数，为每个任务t学习不同的动态网络 $f{θ_t}（-）$。**

我们假设代理人有有限的内存，并且不能访问跨任务的状态转换数据。因此，在每个任务 $t$ 开始时，特定任务的重放缓冲器 $Dt$ 被重置。对于当前的情节，代理人使用 $θ_t=H{Θt}（e_t）$生成一个动力学网络 $f{θt}$。然后，对于 $k=1…K$个时间段和规划期限 $h$，代理人使用CEM优化行动序列 $a{k：k+h}$，并执行第一个行动 $ak$（MPC）。$D_t$被一个元组（$s_k$,$a_k$, $s{k+1}$）所增强，其中 $sk$ 是当前状态，$a_k$是已执行的行动，$s{k+1}$是任务t下的下一个观察状态。

超网络的参数 $Θt$ 和任务嵌入 $e_t$ 通过反向传播梯度更新，涉及动态损失 $L{dyn}$和正则化项之和。

我们定义了动态损失 $L{dyn}(\theta_t, e_t) = \sum{Dt}||\hat s{k+1} - s{k+1}||_2$ , 预测的下一状态在哪里 $\hat s{k+1} = f{\theta_t}(s_k, a_k)$ 和 $\theta_t = H{\theta_t}(e_t)$

$\hat s{k+1}=f{\thetat}(s_k,a_k)$ 和 $\theta_t = H{\theta_t}(e_t)$

超网络的规范化:

为了减轻灾难性的遗忘，我们对超网络的输出进行正则化，即所有以前的任务嵌入 $e{1:t-1}$。在对任务 $t-1$进行训练后，超网络权重的快照被保存为 $Θ{t-1}$。

对于每个过去的任务 $i = 1…t - 1$，我们使用正则化损失来保持快照 $H{Θ_t} (e_i)$的输出接近当前输出 $H{Θt} (e_i)$。这种方法避开了存储所有过去任务数据的需要，保留了动态网络 $f{θt}$的预测性能，并且只需要存储权重空间中的一个点（超网络的副本）。任务嵌入是与超网络的参数一起学习的可微分向量。更新 $Θ_t$和 $e_t$ 的总体损失函数由动态损失 $L{dyn}(-)$和正则化项$L_{reg}(-)$组成，动态损失是根据任务 $t$ 收集的数据评估的:

$$L_t(\theta_t, e_t) = L_{dyn}(\theta_t, e_t) + L_{reg}(\theta_{t-1}, \theta_t, e_{1:t-1})$$ $$L_{reg}(\cdot) = \frac{\beta_{reg}}{t-1}\sum_{i=1}^{t-1}||H_{\theta_{t-1}}(e_i) - H_{\theta_t}(e_i)||_2^2$$

CEM优化行动序列的计划目标是由在学习到的任务动力学模型 $f{θ_t}(-)$下执行行动序列 $a{k:k+h}$得到的奖励之和给出的。奖励函数 $r(s,a)$ 被假定为已知的，但在我们目前的框架下，没有什么可以排除从数据中学习它。

Hypernetworks for Continual Semi-Supervised Learning

从顺序到达的数据中学习，可能在非 i.i.d. 方式，随着时间的推移不断变化的任务分配被称为持续学习。 迄今为止，持续学习的大部分工作都集中在监督学习上，而最近的一些工作则集中在无监督学习上。

在许多领域，每个任务都包含标记（通常很少）和未标记（通常很多）的训练示例，这需要半监督学习方法。 为了在持续学习环境中解决这个问题，我们提出了一个半监督持续学习的框架，称为持续半监督学习的元合并 (MCSSL)。

我们的框架有一个超网络，它学习生成作为基础网络的半监督辅助分类器生成对抗网络（Semi-ACGAN）的权重的元分布。 我们在超网络中巩固序列任务的知识，基础网络学习半监督学习任务。 此外，我们提出了 Semi-Split CIFAR-10，这是一个用于持续半监督学习的新基准，通过修改 Split CIFAR-10 数据集获得，其中带有标记和未标记数据的任务按顺序到达。 我们提出的模型在持续的半监督学习环境中产生了显着的改进。 我们比较了几种现有的持续学习方法在 Semi-Split CIFAR-10 数据集提出的持续半监督学习基准上的性能。

Introduction

人类拥有非凡的持续学习能力，即使在顺序设置中也是如此。 在机器学习中，从可能以非 i.i.d. 连续到达的数据中学习。 使任务随时间变化的方式称为持续学习、终身学习或增量学习。 人类学习的另一个突出方面是人类并不总是需要对对象的概念进行监督，他们可以通过对相似的事物进行分组来学习。 相比之下，神经网络在以顺序方式学习新任务时表现出忘记先前获得的知识的趋势 [Kirkpatrick et al., 2017]，这通常被称为灾难性遗忘。

随着数据的日益多样化，缺乏标记数据是监督机器学习模型面临的一个普遍问题。 然而，未标记的数据很丰富，并且很容易用于训练机器学习模型。 在标准（非连续）环境中，存在几种无监督学习方法，它们可以在没有监督的情况下基于某种相似性概念进行学习。 然而，半监督学习模型可以利用标记和未标记的数据，从而实现两全其美。

大多数现有的持续学习方法都集中在监督分类设置上。 最近的一些工作探索了持续的无监督学习设置 [Lee et al., 2019; Rao et al., 2019] 专注于图像生成任务的生成模型。

然而，这些方法中的大多数都没有研究半监督的持续学习设置。 [Smith et al., 2021] 最近的一项工作探索了连续半监督设置，但他们的设置使用了 CIFAR 数据集的超类结构，因此，顺序到达的任务与我们的设置不同 . 此外，他们的方法使用判别分类器，而我们的方法使用生成模型，因为模型学习输入的分布。

因此，我们研究了一种用于连续半监督学习的新设置，其中连续学习器遇到带有标记和未标记数据的顺序到达任务。 与标准的半监督学习设置类似，未标记数据和标记数据在每个学习任务中具有内在相关性，使学习者能够利用标记数据和未标记数据。

大多数持续学习方法通过在权重（或参数）空间或数据空间中巩固知识来对抗灾难性遗忘。 根据对人脑的研究，语义知识或解决任务的能力表示在高级语义概念的元空间中。

此外，记忆会定期巩固，帮助人类持续学习 受此启发，[Joseph and Balasubramanian, 2020] 最近的工作提出了一个框架，即持续学习的元巩固 (MERLIN)，它巩固了持续任务的知识 在元空间中，即权重生成网络的参数空间。 这个权重生成网络称为超网络，它生成基础网络的参数。 这样一个基础网络负责解决特定的不断到达的下游任务。 我们在 [Joseph and Balasubramanian, 2020] 中使用具有特定任务先验的变分自动编码器 (VAE) 模型对超网络进行建模。 然而，他们只关注监督学习设置。 因此，基础网络是判别神经网络，例如前馈神经网络或改进的残差网络 (ResNet-18)。

在本文中，我们提出了 MCSSL: Meta-Consolidation for Continual Semi-Supervised Learning，这是一个源自 MERLIN [Joseph and Balasubramanian, 2020] 的框架，其中持续学习发生在权重生成过程的潜在空间中，即 ，在超网络的参数空间中。 然而，[Joseph and Balasubramanian, 2020] 使用判别分类器 (ResNets) 作为基础网络，因此他们只关注持续监督设置。与 [Joseph and Balasubramanian, 2020] 相比，我们的模型使用改进形式的辅助分类器生成对抗网络 (ACGAN) [Odena et al., 2017] 作为基础网络来执行持续的半监督学习。 GAN 中的辅助分类器提供了使用标记数据学习分类的能力。 受 [Salimans et al., 2016] 的启发，我们修改了 ACGAN 中的判别器来处理未标记的数据，我们称之为 Semi-ACGAN。 这导致在 Semi-ACGAN 训练目标中具有监督和非监督组件。 因此，类 VAE 的超网络学习生成 Semi-ACGAN 基础网络的参数，该基础网络执行半监督分类的下游任务。

MCSSL: Meta-Consolidation for Continual Semi-Supervised Learning

本节从持续半监督学习的问题设置开始。 在此之后，我们介绍了我们提出的框架的概述。 然后，我们将 Semi-ACGAN 描述为基本模型和 Semi-ACGAN 的训练机制。 此外，我们提供了学习特定任务参数分布的超网络 VAE 的详细信息。 此外，我们描述了超网络元整合的细节，然后是推理机制。

Problem Set-up and Notation

持续半监督学习的问题涉及从顺序到达的半监督任务中学习，因为任务的数据仅在前一个任务完成后到达。 令 $T_1、T_2、···、T_K$ 为半监督任务序列，使得 $T_k$ 为时间实例 k 处的任务。

此外，对于 $j ∈{1,····,K}$，每个任务 $T$ 由 $T^{tr}_j$、$T^{val}_j$ 和 $T^{test}_j$ 组成，分别对应于任务 $j$ 的训练集、验证集和测试集。此外，我们定义

$$T^{tr} = [\{x_m,y_m\}^{M^j_{tr}}_{m=1}, \{u_n\}^{N_{tr}^j}_{n=1}]$$

Model Overview

在我们提出的框架中，超网络是一个类似于 VAE 的模型，具有特定于任务的条件先验，它对基础网络的参数分布进行建模。 对于每个任务，基础网络的多个实例使用标记和未标记的训练数据来学习下游半监督任务。 我们使用这些训练过的基础模型的权重作为训练超网络的输入。 因此，超网络学习为基础网络生成任务特定的权重，最终执行连续的半监督任务。 此外，元整合使超网络能够整合来自先前任务的知识。 此外，在训练之后，在预测或推理期间对基础网络的权重进行采样和集成。

Base Model: Semi-ACGAN

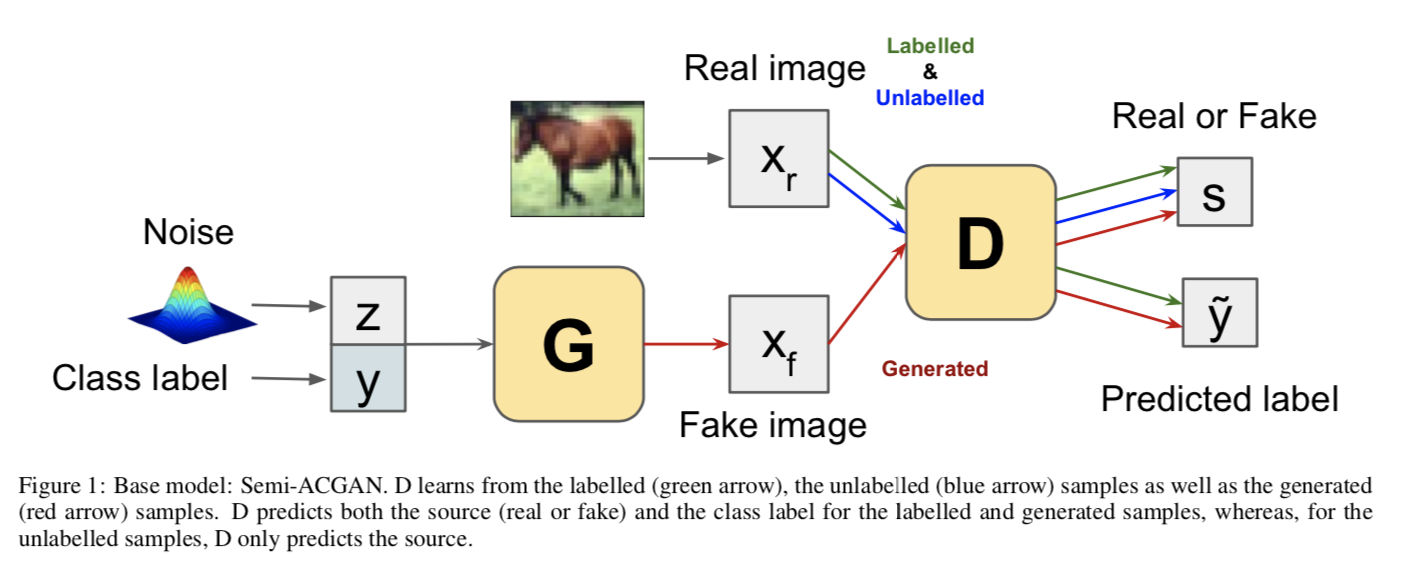
基础网络是一个改进的辅助分类器 GAN (Semi-ACGAN)，因此由一个生成器 G、一个带有辅助分类器的鉴别器 D 组成。 我们使用 $Θ_k$ 表示任务 k 的基础网络的权重。

在 Semi-ACGAN 中，G 以类标签 y 和噪声 $zb$ 为条件。 因此，生成的样本 $x{fake} = G(z_b,y)$ 对应于一个类标签。让 s 表示样本 x 的来源是真实的还是虚假的。 对于样本 x，判别器给出源 $p(s|x)$ 上的概率分布以及类 $p(y|x)$ 上的概率分布，即 $[p(s|x), p(y| x)] = D(x)$。

让我们用 $x_{real}$ 表示真实样本，用 $\hat y$ 表示样本的实际类别。 训练目标包括以下内容：

• 对于标记数据：

• • a.记录正确来源的可能性，

  • $$L_s^{L} = E[\log p(s=real|x_{real})] +E[\log p(s=fake|x_{fake})]$$

  • b.记录正确类别的可能性，

  • $$L_c^L=E[\log p(y=\hat y|x_{real})] + E[\log p(y=\hat y|x_{fake})]$$

• 对于无标注数据：

• • a. 记录真实图像正确来源的可能性，

  • $$L_s^{U} = E[\log p(s=real|x_{real})]$$

鉴别器 D 通过最大化 $L^L_c + L^L_s + L^U_s$ 来学习，而生成器 G 通过最大化 $L^L_c - L^L_s$ 来学习。

请注意，由于缺少未标记数据的类别信息，因此我们不考虑未标记数据情况下正确类别的对数似然。

生成器 G 是一个接受类标签和噪声的神经网络。 类标签嵌入是使用可训练的类嵌入层从类 id 获得的。 因此，G 学习生成特定类别的样本。

D 的共享层可以从标记数据和未标记数据中学习。 随着训练的进行，G 学习生成具有已知类标签的真实样本，使 D 能够进行更好的分类。

图 1 显示了基础网络 Semi-ACGAN 的模块。 由于真实样本可以由标记数据和未标记数据组成，图中分别使用绿色和蓝色箭头显示。 另一方面，红色箭头描绘了生成的样本。 此外，输出以类似的颜色编码。

Task-specific Parameter Distribution: Hypernetwork

由于训练过的基础网络的 B 个实例被用作训练超网络的输入，我们使用 ${Θ^lk}^B{l=1}$ 来表示任务 k 的这个集合。 由于使用具有特定任务条件先验的 VAE 类模型作为超网络，我们将超网络的参数定义为 $[θ, φ]$，使得 $θ$ 和 $φ$ 分别是超网络的编码器和解码器参数 .

超网络 VAE 对特定于任务的参数分布 $p(Θ|t)$ 进行建模。 因此，学习超网络可以整合元空间中先前任务的知识。 第 k 个任务的向量表示 $t_j$ 可以是任何固定长度的向量表示，包括 Word2Vec [Mikolov et al., 2013]、GloVe [Pennington et al., 2014] 或只是任务标识的 one-hot 编码。 为简洁起见，我们在本小节中使用 $t$ 来表示 $t_j$。

受 MERLIN [Joseph and Balasubramanian, 2020] 的启发，超网络通过优化类似 VAE 的目标 [Kingma and Welling, 2013] 进行训练。

参数分布 $pθ (Θ|t) = \int pθ (Θ|z, t)pθ (z|t)dz$ 的边际似然的计算是难以处理的，因为其真实后验 $p{\theta}(z|Θ,t)=\frac{p{\theta}(Θ|z,t) p{\theta}(z|t)}{p_{\theta}(Θ|t)}$ 的计算难以处理。

因此，我们引入了一个近似变分后验 $q_\phi(z|Θ,t)$ 来解决难以处理的问题。 对数边际似然可以写成：

$$p_{\theta}(Θ|t) = KL(q_{\phi}(z|Θ,t) || p_{\theta}(z|Θ,t) + L(\theta,\phi|Θ,t)$$

其中 $L(\theta,\phi|\theta,t) = \intz q{\phi}(z|Θ,t)\log \frac{p{\theta(z,Θ|t)}}{q{\phi}(z|Θ,t)}$ 是证据下限 (ELBO)。 为了最大化对数似然，可以最大化这个下限。

此外，$L(θ, φ|Θ, t)$ 可以表示为（完整推导参见[Joseph and Balasubramanian, 2020]）：

$$L(θ, φ|Θ, t) = -KL(q_{\phi}(z|Θ,t) || p_{\theta}(z|t) + E_{q_{\phi(z|Θ,t)}}[\log p_{\theta}(Θ|z,t)])$$

最大化上面方程，最小化 KL 散度项，导致近似后验权重变得接近于特定任务的先验 $p_θ(z|t)$。 第二项是预期的负重构误差，它需要抽样来估计。

超网络参数 φ 和 θ，也称为编码器和解码器参数，使用反向传播和随机梯度下降进行训练。 我们假设 $pθ (.)$ 和 $qφ (.)$ 是高斯分布。此外，重新参数化技巧 [Kingma and Welling, 2013] 用于通过随机参数进行反向传播。 以 ${Θ^lk}^B{l=1}$ 作为输入，我们通过最大化 上式 来训练超网络。

与标准 VAE 不同，特定于任务的先验不是各向同性的多元高斯。 它由以下给出：

$$p_{\theta}(z|t) = N(z|\mu_t,\Epsilon_t)$$

其中 $\mut = W^T{\mu} t$ 和 $\Epsilont = W^T{\Epsilon}t$ 这样 $Wμ$ 和 $WΣ$ 是可训练的参数，并与超网络参数一起学习。

Meta-Consolidation

直接在 ${Θ^lk}^B{l=1}$ 上训练 VAE 会导致分布偏移，即偏向当前任务 $k$。 因此，超网络 VAE 需要巩固来自先前任务的知识。我们称之为元整合。 我们存储所有学习到的特定于任务的先验的均值和协方差，这增加了可以忽略不计的存储复杂性。 元整合机制描述如下：

1.对于直到当前任务 $k (j=1,…,k) $的每个任务 $z_{t_j}$，

• (a) 来自特定任务的先验样本 $z_{t_j }$：

  $$z_{t_j} \sim N(z|\mu_{t_j}, \Epsilon_{t_j})$$

• (b) 从解码器中采样 P 个半监督基础伪模型：

  $$Θ_j^i \sim p_{\theta}(Θ|z_{t_j}, t_j); \ where \ \ i\in\{1,2,...,P\}$$

• (c)使用公式5计算损失：

  $$Loss = \sum_{i=1}^P L(Θ,\phi|Θ^i_j,t_j)$$

• (d)优化 Loss 以更新参数φ，θ

Inference

学习特定于任务的参数分布 $p_θ(Θ|z,t)$ 可以在推理过程中对多个 $Θ$ 进行采样。 这种能力提供了多个模型的集成效果，而无需先验地存储模型。 与大多数其他持续学习方法一样，我们在推理过程中使用一个小的示例内存缓冲区 $\epsilon$ 进行微调。

我们的方法可以在推理过程中使用或不使用特定于任务的信息。 然而，我们专注于与任务无关的设置，因为它更加现实和具有挑战性。 任务无关推理的推理过程如下所述：

HYPERMODELS FOR EXPLORATION

我们考虑由参数空间 $θ$ 的元素 $θ$ 参数化的基本模型。 给定 $θ$ ∈ $Θ$ 和输入 $Xt ∈ R^{N_x}$ ，基本模型假设输出 $Y{t+1} ∈ R$ 的条件期望由 $E[Y{t+1}|X_t,θ] = fθ(X_t)$ 给出，对于某些函数 f 由 θ 索引。 图 1a 描述了这类参数化基础模型。

超模型由参数 ν 参数化，参数 ν 标识函数 $g_ν : Z 􏰝→ Θ$。我们将每个 z ∈ Z 称为索引，因为它标识了基本模型的特定实例。 特别是，给定超模型参数 ν，可以通过选择 z ∈ Z 并设置 θ = gν (z) 来生成基本模型参数 θ。

这种超模型的概念如图 1b 所示。 与超模型一起，为了表示基础模型上的分布，我们必须指定一个参考分布 $p_z$，它可用于对 Z 的元素进行采样。超模型和参考分布通过提供一种机制共同表示基础模型上的分布 通过对索引进行采样并通过映射对其进行采样。