Model-Agnostic Meta-Learning for Fast Adaptation of Deep Networks

MAML一种模型无关的元学习算法，即它可以与任何经过梯度下降训练的模型兼容，并适用于各种不同的学习问题，包括分类、回归和强化学习。

元学习的目标是在各种学习任务上训练一个模型，它只需要少量的训练样本就可以解决新的学习任务。

MAML模型的参数被显式地训练，使得少量的梯度步骤和来自新任务的少量训练数据将在该任务上产生良好的泛化性能，易于微调。

核心思想是训练模型的初始参数，以便在参数通过一个或多个梯度步骤更新后，模型在新任务上具有最大性能，该梯度步骤使用来自该新任务的少量数据计算。

这种快速灵活的学习是一种挑战，因为模型必须将其先前的经验与少量新信息相结合，同时避免过拟合新数据。此外，先验经验和新数据的形式将取决于任务。因此，为了获得最大的适用性，learn to learn (或元学习)的机制应该适用于任务和完成任务所需的计算形式。

Model-Agnostic Meta-Learning

目标是训练能够实现快速适应的模型，这是一种通常被形式化为few-shot learning的问题设置。

Meta-Learning Problem Set-Up

few-shot learning元学习的目标是训练一个只使用几个数据点和训练迭代就能快速适应新任务的模型。

实际上，元学习问题将整个任务视为训练示例。

定义一个模型为f，它将观测值 $x$ 映射到输出 $a$ 。在元学习期间，模型被训练成能够适应大量或无限数量的任务。

定义每个任务 $T = {L(x1,a_1,…,x_H,a_H) , q(x_1), q(x{t+1}|x_t,a_t ), H}$

$L$ 是loss function，初始观测 $q(x1)$ 的分布，通过$q(x{t+1}|x_t,a_t)$ 转换分布，事件长度$H$

在独立同分布的有监督学习问题中，长度H=1。该模型可以通过在每个时间步 $t$ 选择一个输出来产生长度为 $H$ 的样本。Loss函数提供任务特殊的反馈。

在元学习场景中，我们考虑希望模型能够适应的任务$p(T)$上的分布。在 K-shot 学习设置中，该模型被训练成仅从$qi$ 中提取的K个样本和由任务 $T_i$ 生成的反馈 $L{T_i}$ 中学习 从$p(T)$中提取的新任务$T_i$。

在元训练过程中，从 $p(T)$ 中抽取一个任务 $Ti$，用K个样本训练模型，并从$T_i$中相应的$L{T_i}$ 损失反馈，然后在$T_i$的新样品上进行测试。然后，通过考虑来自 $q_i$ 的新数据上的测试误差如何相对于参数变化来改进模型 $f$。

实际上，采样任务 $T_i$ 上的测试误差充当元学习过程的训练误差。在元训练 (meta-training)结束时，从$p(T)$采样新任务，从K个样本中学习后，通过模型的性能来衡量元性能(meta-performance)。一般来说，元测试 (meta-testing) 任务是在元训练 (meta-training) 期间执行的。

A Model-Agnostic Meta-Learning Algorithm

我们怎样才能鼓励这种通用型代表的出现呢？例如，神经网络可能学习广泛适用于 $p(T)$ 中所有任务的内部特征，而不是单个任务。

MAML对这个问题采取了明确的方法：由于模型将在新任务上使用基于梯度的学习规则进行微调，因此我们的目标是学习一个模型，使此基于梯度的学习规则能够在从$p(T)$提取的新任务上取得快速进展，而不会过拟合。

实际上，我们的目标是找到对任务变化敏感的模型参数，以便参数的微小变化将在沿损失梯度方向改变时，对从 $p(T)$ 得出的任何任务的损失函数产生较大的改进。如下图：

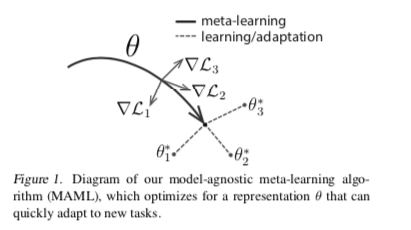
我们对模型的形式不做任何假设，只是假设它由一些参数向量 $θ$ 参数化，并且损失函数在 $θ$ 中足够平滑，因此我们可以使用基于梯度的学习技术。

定义这个参数化的模型为$f_{\theta}$ , 参数为$\theta$。 当适应一个新的任务$T_i$时，模型的参数 $θ$ 变为 $θ_i’$。

使用任务 $T_i$ 上的一个或多个梯度下降更新来计算更新后的参数向量 $θ_i’$。例如，当使用一个梯度更新时:

$$\theta_i' = \theta - \alpha \nabla_{\theta}L_{T_i}(f_{\theta})$$

步长 $α$ 可以固定为超参数。

通过优化 $f_{θ_i’}$相对于从 $p(T)$ 采样的任务的 $θ$ 的性能，来训练模型参数。更具体地说，元目标如下：

$$min_{\theta} \sum_{T_i\sim p(T)} L_{T_i}(f_{\theta_i'}) = \sum_{T_i\sim p(T)} L_{T_i}(f_{\theta - \alpha \nabla_{\theta}L_{T_i}(f_{\theta})})$$

注意，元优化 （meta-optimization）是在模型参数θ上执行的，而目标是使用更新后的模型参数 $θ’$来计算的。实际上，MAML提出的方法旨在优化模型参数，使得新任务上的一个或少量梯度步骤将在该任务上产生最有效的行为。

跨任务的元优化通过随机梯度下降（SGD），模型参数θ更新如下：

$$\theta \leftarrow \theta - \beta \nabla_{\theta} \sum_{T_i \sim p(T)} L_{T_i}(f_{\theta_i’})$$

$β$ 是元步长。下图概述了一般情况下完整的算法：

输入任务不同分布的任务$p(T)$ 和两个学习步长超参数 $\alpha, \beta$ ,并且随机初始化模型参数。

第一层循环，遍历每个任务 $T_i \sim p(T)$ 中采样的batch

第二层循环，在每个任务 $Ti$ 中 评估关于 K 个样本的 $∇θ L{T_i}(fθ)$ 使用梯度下降计算自适应参数：$θi’ = θ − α\nablaθL{T_i}(fθ)$

然后根据所有任务上的损失梯度更新模型的参数 $\theta \leftarrow \theta - \beta \nabla{\theta} \sum{Ti \sim p(T)} L{Ti}(f{\theta_i’})$

MAML元梯度更新涉及通过梯度的梯度, 在计算上，这需要额外的反向传播 $f$ 来计算Hessian-vector乘积。

Species of MAML

监督学习和强化学习的元学习算法的具体实例。他们在损失函数的形式以及数据由任务生成并呈现给模型的方式上不同。

Supervised Regression and Classification

Few-shot 学习在监督任务领域得到了很好的研究，其目标是仅从该任务的几个输入/输出对中学习新函数，使用类似任务的先前数据进行元学习。

我们可以定义horizon H=1并将timestep下标放到 $x_t$上，因为模型接受单个输入并生成单个输出，而不是一系列输入和输出。

任务 $T_i$ 从 $q_i$生成K个观测值 $x$ ，并且任务损失由模型的输出 $x$ 与该观测值和任务对应的目标值 $y$ 之间的误差表示。

用于监督分类和回归的两种常见损失函数是交叉熵和均方误差(MSE)，对于使用均方误差的回归任务，损失形式为：

$$L_{T_i}f(\phi) = \sum_{x^{(j)},y^{(y)} \sim T_i} ||f_{\phi}(x^{(j)}) - y^{(j)}||_2^2$$

其中 $x^{(j)}, y^{(j)}$ 是任务$T_i$的一对输入输出，类似地，对于具有交叉熵损失的离散分类任务，损失采取以下形式：

$$L_{T_i}f(\phi)= \sum_{x^{(j)},y^{(y)} \sim T_i} y^{(j)} log f_{\phi}(x^{(j)}) + (1-y^{(j)})log(1-f_{\phi}(x^{(j)}))$$

Reinforcement Learning

在强化学习（RL）中，Few-shot 元学习的目标是使模型能够仅使用测试设置中的少量经验快速获取新测试任务的策略。

例如，一个模型可能会学习如何快速找到如何导航迷宫，以便在面对新的迷宫时，只需几个样本就可以确定如何可靠地到达出口。

每个RL 任务$Ti$ 包含一个初始化状态分布$q_i(x_1)$ 和一个转换分布 $q_i(x{t+1}| xi,a_t)$ , 损失函数为 $L{T_i}$

因此，整个任务是一个具有horizon H的马尔可夫决策过程（MDP），在该过程中，学习者可以查询有限数量的样本轨迹以进行少量镜头学习。

MDP的任何方面都可以在 $p(T)$ 中的任务之间改变。正在学习的模型 $f_θ$ 是一个策略，它从状态 $x_t$映射到每个操作上的分布时间步长 $t∈{1，.，H}$。任务$T_i$ 的模型的损失:

$$L_{T_i}(f_\phi) = -\mathbf{E} _{x_t,a_t\sim f_{\phi},q_{T_i}} [\sum_{t=1}^H R_i(x_t, a_t)]$$

实验

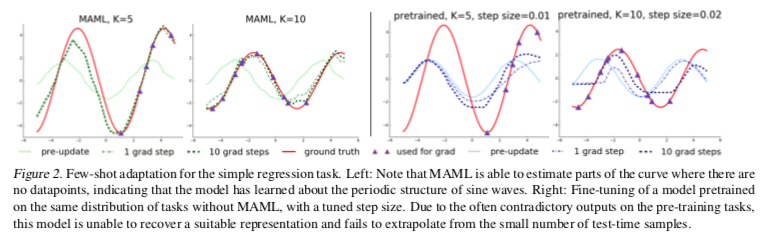
MAML能实现新任务的快速学习吗？

MAML是否可以用于多个不同领域的元学习，包括有监督的回归、分类和强化学习？

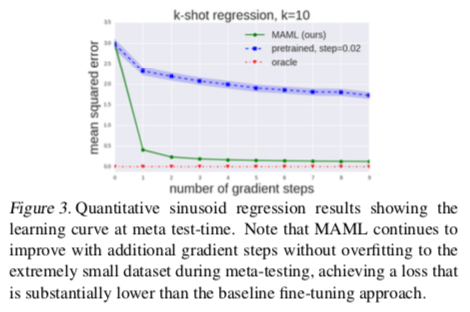
用MAML学习的模型可以通过额外的渐变更新和/或示例继续改进吗？