Attention
从RNN到LSTM到Transformer再到GNN
RNN
LSTM
Attention
单头注意力
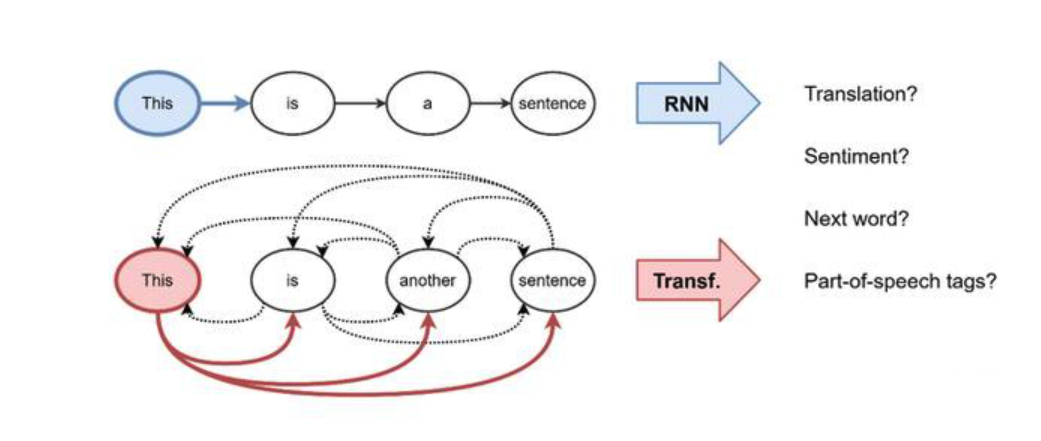
将句子 $S$ 中第 $i$ 个词的隐藏特征 $h$ 从 $l$ 层更新到 $l+1$ 层 :
$Q^l, K^l , V^l$ 是可学习的线性权重(分别表示注意力计算中的Query,Key,Value)。句子中的每个单词并行执行注意力机制,从而可以一次性获得他们已更新的特征——这是Transformer相对RNNs的另一个加分点,它使得模型能够逐字更新特征。
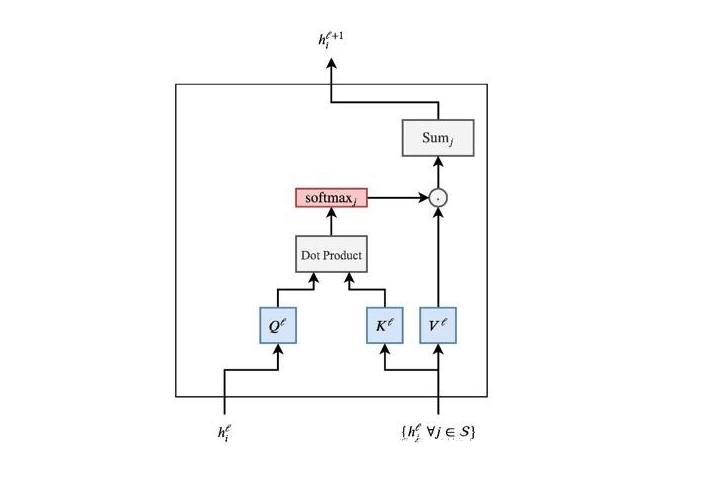
多头注意力
事实证明,要让这种点积注意力机制起作用是很难的——如果随机初始化处理得不好会使得整个学习过程失去稳定性。我们可以通过并行执行多个注意力“头”并将结果连接起来(现在每个注意力头都有单独的可学习权重)来克服这个问题:
其中, $Q^{k,l} ,K^{k,l}, V^{k,l}$ 是第 $k$ 个注意力投的可学习权重,而 $O^l$ 是一个向下的投影,可以用以匹配跨层的 $h_i^{l+1}$ 和 $h^l_i$ 的尺寸。此外多头注意力形成多个子空间,可以让模型去关注不同方面的信息。
Transformer架构
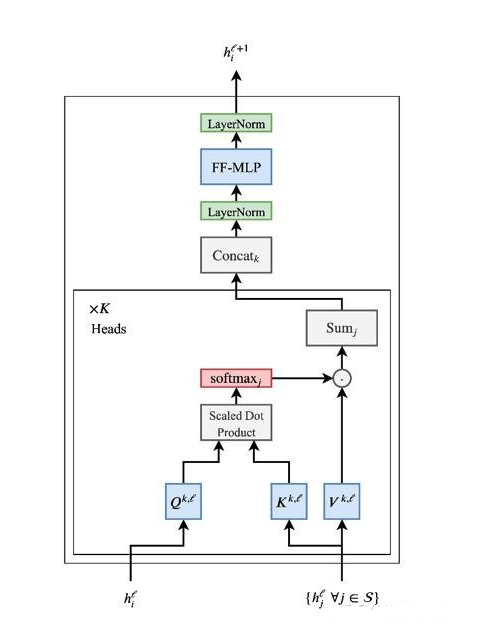
下面是上文的多头Attention结构,但为什么Transformer的结构为什么是这样的?
注意力机制之后的词的特征可能在不同尺度或重要性上:
这可能是由于某些词在将其他词的特征累加时具有非常集中或非常分散的注意力权重 $w_{ij}$
在单个特征/向量输入级别,跨多个注意力头 (每个可能会以不同的比例输出值) 进行级联可以导致最终向量 $h_i^{l+1}$ 的输入具有一个大范围的值。遵循传统的机器学习思路,在上述流程中增加一个归一化层似乎是合理的选择。
对于上面的两个问题,Transformer用LayerNorm客服了问题2,LayerNorm在特征层级上进行归一化并学习一种仿射变换。 batchNormalization与layerNormalization的区别
对于问题1,通过求特征维度的平方根,来做缩放点积。
在LayerNorm之后,是FF-MLP
是一个控制尺度问题的技巧,具有特殊结构的考虑位置的双层MLP,在多头注意力之后,他们通过一个可学习的权重将 $h_i^{l+1}$ 投影到一个更高的维度,在该维度中, $h_i^{l+1}$ 经过ReLU 非线性变换,然后投影回其原始维度,然后再进行另一个归一化操作。
不确定超参数化前馈子层背后的确切理由是什么,似乎也没有人对此提出疑问!我认为LayerNorm和缩放的点积不能完全解决突出的问题,因此大型MLP是一种可以相互独立地重新缩放特征向量的手段。
Transformer架构也非常适合非常深的网络,使NLP界能够在模型参数和扩展数据这两方面进行延伸。每个多头注意力子层和前馈子层的输入和输出之间的残差连接是堆叠Transformer层的关键(但为了清楚起见,在上图中省略了)。
GNN
图神经网络(GNNs)或图卷积网络(GCNs)在图数据中建立节点和边的表示。它们是通过邻域聚合(或消息传递)来实现的,在邻域聚合中,每个节点从其邻域收集特征,以更新其周围的局部图结构表示。通过堆叠多个GNN层使得该模型可以将每个节点的特征传播到整个图中,从其邻居传播到邻居的邻居,依此类推。
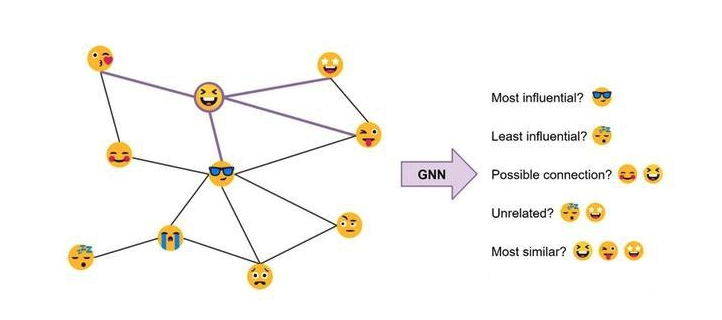
以这个表情符号社交网络为例:由GNN产生的节点特征可用于预测性任务,例如识别最有影响力的成员或提出潜在的联系。
在他们最基本的形式中,GNNs通过以下方法来更新节点 $i$ 在 $l$ 层的隐藏层特征 $h$ 。
也就是先将节点自身特征 $h_i^{l}$ 和每个邻居节点 $j \ \ (j\in N(i))$ 特征 $h_j^{l}$ 的聚合相加,然后在整体做一个非线性变换, 如下:
其中, $U^l, V^l$ 是GNN 层的可学习权重矩阵。
邻居节点 $j\in N(i)$ 上的求和可以被其他输入大小不变的聚合函数代替,例如简单的 均值/最大值函数或其他更强大的函数(如通过注意机制的加权和)。
如果是GAT的话其实就变成了Transformer了
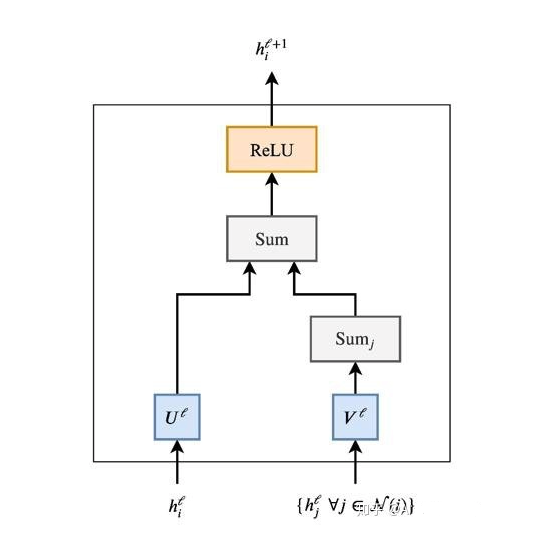
如果我们要执行多个并行的邻域聚合头,并且用注意力机制(即加权和)替换领域 上的求和 ,我们将获得图注意力网络(GAT)。加上归一化和前馈MLP,瞧,我们就有了Graph Transformer!
在NLP中,句子就是由词全连接而成的图
为了使连接更加清晰,可以将一个句子看作一个完全连接的图,其中每个单词都连接到其他每个单词。现在,我们可以使用GNN来为图(句子)中的每个节点(单词)构建特征,然后我们可以使用它来执行NLP任务。
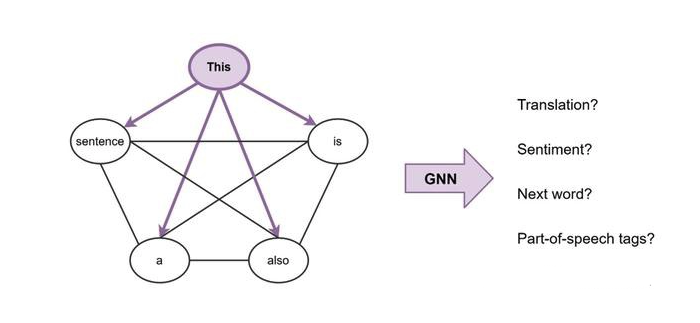
广义上来讲,这就是Transformers正在做的事情:Transformers是以多头注意力作为邻聚合函数的GNNs。标准GNNs从其局部邻域节点 $j\in N(i)$ 聚合特征,而NLP的Transfors 将整个句子视为局部邻域,在每个层聚合来自每个单词 $j\in S$的特征。 而NLP的Transformers将整个句子视为局部邻域,在每个层聚合来自每个单词 $j\in S$ 的特征。
重要的是,各种特定于问题的技巧(如位置编码、因果/掩码聚合、学习率表和大量的预训练)对于Transformers的成功至关重要,但在GNN界中却很少出现。同时,从GNN的角度看Transformers可以启发我们摆脱模型结构中的许多花哨的玩意。
全连接图是NLP的最佳输入格式吗?
在统计NLP和ML之前,Noam Chomsky等语言学家致力于发展语言结构的最新理论,如语法树/图。Tree LSTMs已经尝试过这一点,但是也许Transformers/GNNs是可以让语言理论和统计NLP的领域结合得更加紧密的更好的架构?
如何学习到长期依赖?
完全连通图使得学习词与词之间非常长期的依赖关系变得非常困难,这是完全连通图的另一个问题。这仅仅是因为图中的边数与节点数成二次方关系,即在n个单词的句子中,Transformer/GNN 将在 $n^2$ 上对单词进行计算,如果n很大,那将会是一个非常棘手的问题。
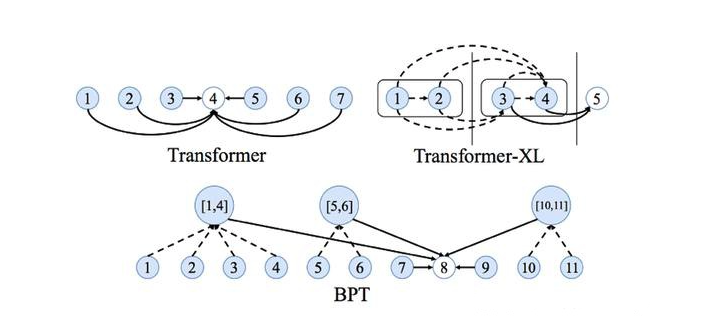
NLP界对长序列和依赖性问题的看法很有意思,例如,使用注意力机制在输入大小方面稀疏或自适应,在每一层中添加递归或压缩,以及使用对局部性敏感的哈希法进行有效的注意,这些都是 优化Transformers 有希望的想法。
有趣的是,还可以看到一些GNN界的想法被混入其中,例如使用句子图稀疏化的二进制分区似乎是另一种令人兴奋的方法。
Transformers在学习神经网络的句法吗?
NLP界有几篇关于Transformers可能学到什么的有趣论文。其基本前提是,对句子中的所有词对使用注意力机制(目的是确定哪些词对最有趣),可以让Transformers学习特定任务句法之类的东西。
多头注意力中的不同头也可能“关注”不同的句法属性。
从图的角度来看,通过在完全图上使用GNN,我们能否从GNN在每一层执行邻域聚合的方法中恢复最重要的边线及其可能带来的影响?我还不太相信这种观点。
为什么要用多头注意力?为什么要用注意力机制?
我更赞同多头机制的优化观点——拥有多个注意力可以改进学习,克服不好的随机初始化。例如,这些论文表明,Transformers头可以在训练后“修剪”或“删除”,并且不会产生重大的性能影响。
多头邻聚合机制在GNNs中也被证明是有效的,例如在GAT使用相同的多头注意力,MoNet使用多个高斯核来聚合特征。虽然多头技巧是为了稳定注意力机制而发明的,但它能否成为提炼出额外模型性能的标准?
相反,具有简单聚合函数(如sum或max)的GNNs不需要多个聚合头来维持稳定的训练。如果我们不需要计算句子中每个词对之间的成对兼容性,对Transformers来说不是很好吗?
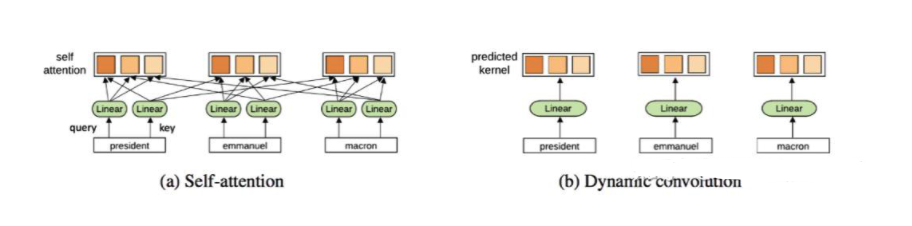
Transformers能从抛弃注意力中获益吗?Yann Dauphin和合作者最近的工作提出了另一种ConvNet架构。Transformers也可能最终会做一些类似于ConvNets的事情。
为什么Transformers这么难训练?
阅读新的Transformer论文让我觉得,在确定最佳学习率表、预热策略和衰减设置时,训练这些模型需要一些类似于黑魔法的东西。这可能仅仅是因为模型太大,而且所研究的NLP任务非常具有挑战性。
但是最近的结果表明,这也可能是由于结构中归一化和残差连接的特定组合导致的。
在这一点上我很在意,但是也让我感到怀疑:我们真的需要代价昂贵的成对的多头注意力结构,超参数化的MLP子层以及复杂的学习计划吗?
我们真的需要具有大量碳足迹的(译者注:有人提出现在训练一个模型相当于5辆汽车一天的排碳量)大规模模型吗?
具有良好归纳偏差的架构难道不容易训练吗?







