Generalizing to Unseen Domains: A Survey on Domain Generalization

机器学习系统通常假定训练和测试分布是相同的。为此，一个关键的要求是开发能够泛化到未见过的分布的模型。近年来，Domain generalization 领域泛化（DG），即 out-of- distribution 泛化，吸引了越来越多的兴趣。

领域泛化处理的是一个具有挑战性的环境，即给定一个或几个不同但相关的领域，目标是学习一个能够泛化到未见过的测试领域的模型。

本文首次对该领域的最新进展进行了回顾。

• 首先，提供了一个领域泛化的正式定义，并讨论了几个相关的领域。
• 然后，彻底回顾了与领域泛化相关的理论，并仔细分析了泛化背后的理论。我们将最近的算法分为三类：数据操作、表征学习和学习策略，并对每一类算法详细介绍了几种流行的算法。
• 第三，介绍了常用的数据集和应用。
• 最后，我们总结了现有的文献并提出了一些未来的潜在研究课题。

INTRODUCTION

传统的ML模型是基于 i.i.d. 假设进行训练的，即训练和测试数据是完全独立分布的。然而，这一假设在现实中并不总是成立。当训练数据和测试数据的概率分布不同时，由于领域分布的差距，ML模型的性能往往会恶化。收集所有可能领域的数据来训练ML模型是昂贵的，甚至是不可能的。因此，提高ML模型的泛化能力在工业和学术领域都很重要。

有许多与泛化相关的研究课题，如领域适应、元学习、迁移学习、covariate shift等等。近年来，领域泛化（DG）受到广泛关注。

如图1所示，领域泛化的目标是从一个或几个不同但相关的领域（即不同的训练数据集）中学习一个模型，该模型将在未见过的测试领域中具有良好的泛化能力。

例如，给定一个由素描、卡通图像和绘画组成的训练集，领域泛化要求训练一个好的机器学习模型，该模型在对来自自然图像或照片的分类中具有最小的预测误差，这些图像显然与训练集中的图像具有不同的分布。

在过去的几年里，领域泛化在计算机视觉和自然语言处理等各个领域都取得了重大进展。尽管取得了这些进展，但在这一领域还没有一份全面介绍和总结其主要思想、学习算法和其他相关问题的调查报告，以提供对未来的研究见解。

在本文中，我们提出了第一份关于领域泛化的调查报告，介绍了它的最新进展，特别关注它的公式、理论、算法、数据集、应用和未来研究方向。我们希望这个调查能够为感兴趣的研究者提供一个全面的回顾，并激发在这个领域和相关领域的更多研究。

• 提出了关于领域泛化和相关领域适应的理论分析。

• 通过增加新的类别：特征分解的生成模型、不变的风险最小化、基于梯度运算的方法和其他学习策略来全面总结这些泛化方法。

• 对于所有的类别，我们通过包括更多的相关算法、比较和讨论，扩大了对不同类别方法的分析。

• 扩展了数据集和应用的范围，同时我们也探索了领域通用的评价标准。

本文的组织结构如下。在第二节中提出了领域泛化的问题并讨论了它与现有研究领域的关系。第三节介绍了领域泛化的相关理论。在第四节中，我们详细描述了一些有代表性的DG方法。第五节介绍了应用，第六节介绍了DG的基准数据集。我们在第七节中总结了现有工作的启示，并提出了一些可能的未来方向。最后，我们在第八节中对本文进行总结。

BACKGROUND

A. Formalization of domain generalization

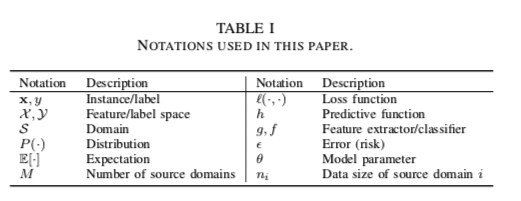
在本节中，我们介绍本文中使用的符号和定义。

Definition 1 (Domain) : X 表示一个非空的输入空间，Y 表示一个输出空间。一个域是由从分布中取样的数据组成的。我们把它表示为 $S = {(xi, y_i)}^n{i=1} \sim P{XY}$ , 其中 $x\in X \subset R^d, y\in Y \subset R$ 表示标签，而 $P{XY}$ 表示输入样本和输出标签的联合分布。X、Y表示相应的随机变量。

Definition 2 (Domain generalization) :

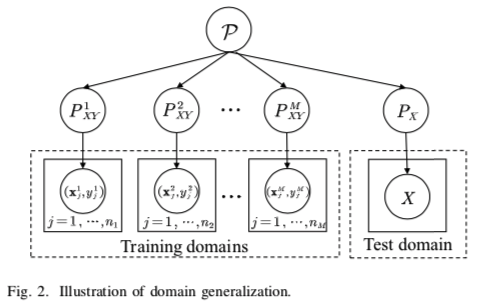
在领域泛化中，我们得到了M个训练（源）的领域 $S{train} = {S^i| i = 1,…,M}$ 其中 $S^i={(x^i_j,y^i_j)}{j=1}^{ni}$ 定义为第 $i$ 个域。每对域的联合分布是不同的：$P{XY}^i \neq P{XY}^j, 1\le i \neq j \le M$ 。域泛化的目标是在 $M$ 个训练域中学习一个稳健的、可泛化的预测函数 $h : X → Y$，以实现对未见过的测试域 $S{test}$ 的最小预测误差（即在训练中不能访问 $S{test}$，$P^{test}{XY}\neq P^i_{XY} i∈{1,…,M}$）:

$$min_h E_{(x,y)\in S_{test}} [l(h(x),y)]$$

其中 $E$ 是期望， $l(\cdot,\cdot)$ 是loss 。我们在表1中列出了常用的记号。

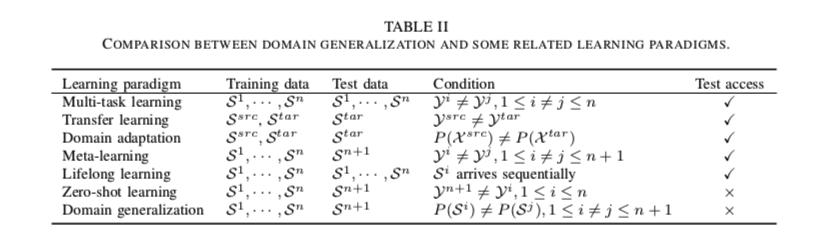
B. Related research areas

有几个研究领域与领域泛化密切相关，包括但不限于：迁移学习、领域适应、多任务学习、多领域学习、元学习、终身学习和 zero-shot 学习。我们在表二中总结了它们与领域泛化的区别，并在下文中简要介绍了它们。

• Multi-task learning ：联合优化了几个相关任务的模型。通过在这些任务之间共享表征，我们可以使模型在原来的任务上有更好的泛化能力。请注意，多任务学习的目的不是为了加强对新的（未见过的）任务的泛化。特别是，多领域学习是一种多任务学习，它在多个相关领域进行训练，为每个原始领域而不是新的测试领域学习好的模型。
• Transfer learning：在一个源任务上训练一个模型，旨在提高该模型在不同但相关的目标领域/任务上的性能。预训练-微调是转移学习的常用策略，在这种情况下，源域和目标域有不同的任务，目标域在训练中被访问。在DG中，目标域不能被访问，训练和测试任务往往是相同的，而它们的分布是不同的。
• Domain adaptation（DA）：在最近几年也很流行。DA的目的是利用现有的训练源域在给定的目标域上实现性能最大化。DA和DG的区别在于，DA可以接触到目标域的数据，而DG在训练过程中无法看到这些数据。这使得DG比DA更具挑战性，但在实际应用中更现实和有利。
• Meta-learning ：旨在通过学习以前的经验或任务来学习学习者本身，即学会学习。虽然元学习中的学习任务是不同的，但在领域泛化中的学习任务是相同的。元学习是一种通用的学习策略，可以用于DG，通过模拟训练领域中的元训练和元测试任务来提高DG的性能。
• 终身学习，或持续学习：关注的是多个连续领域/任务之间的学习能力。它要求模型通过容纳新的知识，同时保留以前学到的经验，随着时间的推移不断地学习。这也与DG不同，因为它可以在每个时间步骤中访问目标域，而且它没有明确处理跨域的不同分布。
• Zero-shot learning：旨在从已看到的类别中学习模型，并对在训练中未看到的类别的样本进行分类。与此相反，一般来说，领域概括研究的问题是训练和测试数据来自相同的类别，但分布不同。

此外，领域泛化还与 tributionally robust optimization（DRO）有关，其目标是在最坏的分布情况下学习一个模型，希望它能够很好地泛化到测试数据。DRO关注的是优化过程，在领域泛化研究中也可以利用。此外，DG也可以通过数据操作或表征学习方法来完成，这与DRO方法不同。

THEORY

在本节中，我们将回顾一些与领域泛化相关的理论。由于领域适应与领域泛化密切相关，我们从领域适应的理论开始。

A. Domain adaptation

对于一个二元分类问题，我们把源域上的真实标签函数表示为 $h^{∗s} : X → [0,1]$，目标域上的真标签函数为 $h^{∗t}$。让 $h:X →[0,1]$ 是来自假设空间 $H$ 的任何分类器。然后，源域上两个分类器 $h$ 和 $h’$之间的分类误差可以通过以下方式测量 :

$$\epsilon^s(h,h') = E_{x\sim P^s_X} [h(x) \neq h'(x)] = E_{x\sim P^s_X} [|h(x) - h'(x)|]$$

同样地，我们可以定义 $ε^t$，当取 $x∼P^t_X$ 的期望时。定义 $\epsilon^s(h) := \epsilon^s(h,h^{s})$ 并且 $\epsilon^t(h):=\epsilon^t(h,h^{t})$ 作为分类器 $h$ 在源域和目标域上的风险。

DG/DA 的目标是使目标风险 $ε^t(h)$ 最小。但由于我们没有任何关于 $h^{∗t}$ 的信息，所以不容易达到这个目标。因此，人们试图用可操作的源风险 $ε^s(h)$来约束目标风险 $ε^t(h)$。 Ben-David等人给出两种风险的界限：

$$\epsilon^t(h) \leq \epsilon^s(h) +2d_1(P_X^s,P_X^t)+min_{P_{X}\in \{P^s_X,P^t_X\}} E_{x\sim P_X}[|h^{*s}(x) - h^{*t}(x)|]$$

其中 $d1 (P_X^s , P_X^t ) := sup{A∈X} |P_X^s [A] - P_X^t [A]| $ 是两个分布之间的总变化，$\mathbf{X}$ 表示 $X$ 上的 σ场。r.h.s 上的第二项衡量的是两个领域中分布的差异，第三项代表的是标签函数的差异。

然而，总变化是一个强距离（即，它倾向于非常大），可能会使约束（1）松动，并且很难使用有限样本来估计。为了解决这个问题，Ben-David等人开发了另一个约束 ：

$$\epsilon^t(h) \le \epsilon^s(h) + d_{H\Delta H}(P^s_X,P^t_X) + \lambda_H$$

其中，H∆H-divergence 定义为 $d{H∆H}(P_X^s , P_X^t ) := sup{h,h’∈H} |ε^s (h, h’ ) - ε^t (h, h’)|$，取代总变异d1来衡量分布差异，理想联合风险 $λH : = inf{h∈H} [ε^s (h) + ε^t (h)]$ 衡量 $H$ 在两个领域的预测任务中的复杂性。

B. Domain generalization

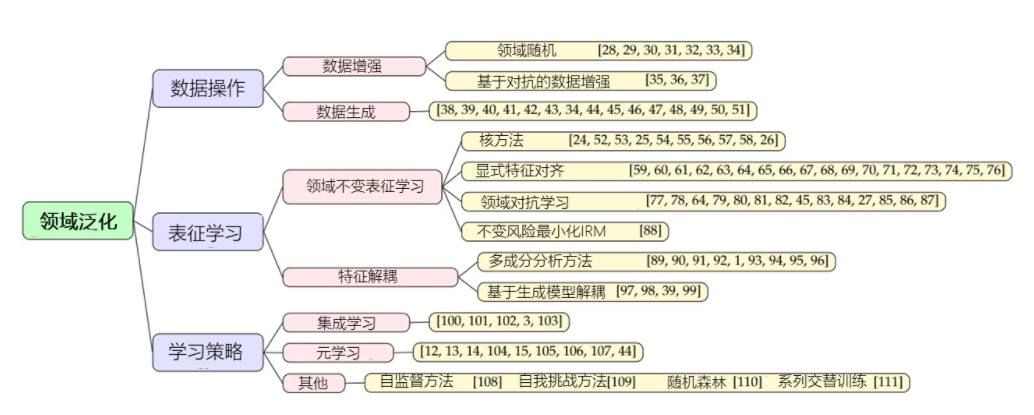
• 数据操作，指的是通过对数据的增强和变化使训练数据得到增强。这一类包括数据增强和数据生成两大部分。
• 表征学习，指的是学习领域不变特征（Domain-invariant representation learning）以使得模型对不同领域都能进行很好地适配。领域不变特征学习方面主要包括四大部分：核方法、显式特征对齐、领域对抗训练、以及不变风险最小化（Invariant Risk Minimiation, IRM）。特征解耦与领域不变特征学习的目标一致、但学习方法不一致，我们将其单独作为一大类进行介绍。
• 学习策略，指的是将机器学习中成熟的学习模式引入多领域训练中使得模型泛化性更强。这一部分主要包括基于集成学习和元学习的方法。同时，我们还会介绍其他方法，例如自监督方法在领域泛化中的应用。

METHODOLOGY

数据操作

在机器学习（ML）中，我们总是渴望得到更多的训练数据。一个ML模型的泛化性能往往依赖于训练数据的数量和多样性。考虑到一组有限的训练数据，数据处理是产生样本的最便宜和最简单的方法之一，这样可以提高模型的泛化能力。基于数据处理的DG的主要目标是使用不同的数据处理方法来增加现有训练数据的多样性。同时，数据数量也会增加。

我们将基于数据操作的DG的总体学习目标制定为：

$$min_h E_{x,y} [l(h(x), y)] + E_{x',y}[l(h(x'),y)]$$

其中 x′=mani(x) 表示使用函数mani(-)操纵的数据。基于这个函数上的差异，我们进一步将现有的工作分为两类：数据增强和数据生成。

1. 基于数据增强的DG：数据增量。扩增是训练机器学习模型的最有用的技术之一。典型的增强操作包括翻转、旋转、缩放、裁剪、添加噪声等等。它们已被广泛用于监督学习中，通过减少过拟合来提高模型的泛化性能[117, 34]。毫无例外，它们也可以被采用于DG，其中mani(-)可以被实例化为这些数据增强函数。

   领域随机化。除了典型的扩增，领域随机化是一种有效的数据扩增技术。它通常通过生成新的数据来完成，这些数据可以在有限的训练样本基础上模拟复杂的环境。随着数据变得更加复杂和多样化，泛化能力可以得到提高。在这里，mani(-)函数被实现为几个手动变换（常用于图像数据），如：改变物体的位置和纹理，改变物体的数量和形状，修改光照和相机视角，以及在数据中加入不同类型的随机噪声。
   Tobin等人[29]首先使用这种方法从模拟环境中产生更多的训练数据，以便在真实环境中进行概括。类似的技术也被用于[30, 31, 32, 28]以加强模型的泛化能力。Prakash等人[33]在随机放置物体进行数据生成时进一步考虑了场景的结构，这使得神经网络在检测物体时能够学会利用上下文。

   抗辩式数据增强。抗辩式数据增强的目的是通过增强数据的多样性，同时保证数据的可靠性，来指导增强工作，优化泛化能力。Shankar等人[35]使用贝叶斯网络来模拟标签、行为和输入实例之间的依赖性，并提出了CrossGrad，这是一种谨慎的数据增强策略，沿最大领域变化的方向对输入进行扰动，同时尽可能少地改变类标签。Volpi等人[36]提出了一个迭代程序，用一个虚构的目标领域的例子来增加源数据集，该领域在当前模型下是 “硬 “的，在每次迭代中都会添加对抗性例子，以实现自适应数据增强。Zhou等人[37]用对抗性训练的转换网络进行数据扩充，而不是直接用梯度上升法更新输入。

2) 基于数据生成的DG：数据生成也是一种流行的技术，可以生成多样化和丰富的数据来提高模型的泛化能力。在这里，函数mani(-)可以使用一些生成模型来实现，如变异自动编码器（VAE）[118]，以及生成对抗网络（GAN）[119]。此外，它也可以使用Mixup[120]策略来实现。
Rahman等人[38]使用ComboGAN[121]来生成新的数据，然后应用领域差异度量，如MMD[122]来最小化真实图像和生成图像之间的分布分歧，以帮助学习一般代表。Qiao等人[39]利用对抗性训练来创建 “虚构 “而又 “具有挑战性 “的人群，其中Wasserstein Auto-Encoder（WAE）[123]被用来帮助生成保留语义并具有大领域转移的样本。Zhou等人[42]在语义一致的情况下生成了新的分布，然后将源分布和新分布之间的差异最大化。Somavarapu等人[43]引入了一个基于图像风格化的简单转换，以探索跨源的可变性，从而实现更好的泛化，其中AdaIN[124]被用来实现快速风格化的任意风格。
除了上述生成模型外，Mixup[120]也是一种流行的数据生成技术。Mixup通过在任何两个实例之间和它们的标签之间进行线性插值，并从Beta分布中抽取权重来生成新数据，这不需要训练生成式模型。最近，有几种方法将Mixup用于DG，通过在原始空间[47, 48]中执行Mixup来生成新的样本；或者在特征空间[49]中，不明确生成原始训练样本。这些方法在流行的基准上取得了很好的性能，同时在概念上和计算上保持简单。

表征学习

几十年来，表征学习一直是机器学习的重点[125]，也是领域泛化成功的关键之一。我们将预测函数h分解为 $h = f ◦ g$，其中g是一个表征学习函数，f是分类器函数。表征学习的目标可以被表述为：

$$min_{f,g} E_{x,g}l(f(g(x)),y) + \lambda l_{reg}$$

其中 $l{reg}$ 表示一些正则化项，λ是权衡参数。许多方法都是为了更好地学习具有相应 $l{reg}$ 的特征提取函数 $g$。在本节中，我们根据不同的学习原理将现有的关于表征学习的文献分为两大类：领域不变的表征学习和特征分解。

1) 基于领域不变表征的DG：[23]的工作从理论上证明，如果特征表征对不同领域保持不变，那么表征就是通用的，可以转移到不同领域（也可以参考第三节）。基于这一理论，人们提出了大量用于领域适应的算法。同样，对于领域泛化来说，目标是减少特定特征空间中多个源域之间的表征差异，使之成为领域不变的，这样学到的模型就能对未见过的领域具有可泛化的能力。按照这一思路，主要有四种方法：基于核的方法、领域对抗性学习、显式特征对齐和不变风险最小化。

**基于核的方法**是机器学习中最经典的学习范式之一。基于核的机器学习依靠核函数将原始数据转化为高维特征空间，而不需要计算数据在该空间的坐标，只需要计算特征空间中所有对的样本之间的内积。最具代表性的基于核的方法之一是支持向量机（SVM）[126]。对于领域泛化，有很多基于核方法的算法，其中表征学习函数g被实现为一些特征映射φ(-)，这很容易用核函数k(-, -)来计算，如RBF核和Laplacian核。

Blanchard等人[24]首次将核方法用于领域泛化，并在[52]中加以扩展。他们采用正半无限核学习，从训练数据中学习一个领域不变的核。Grubinger等人[53]采用转移成分分析法（TCA）[127]来弥补多领域的距离，使之更接近于DG。与TCA的核心思想类似，域不变分量分析（DICA）[25]是使用核进行DG的经典方法之一。DICA的目标是找到一个特征转换核k(-, -)，使特征空间中所有数据之间的分布差异最小。Gan等人[54]采用了与DICA类似的方法，并进一步增加了属性正则化。与处理边际分布的DICA相比，Li等人[55]学习了一种具有领域不变的类条件分布的特征表示。Ghifary等人[56]采用Fisher判别分析法来最小化来自同一类别和同一领域的表示的差异，最大化来自不同类别和不同领域的表示的差异。他们提出了散点成分分析（SCA），使用基于核的方法学习领域不变的表征，其中SCA核考虑了类间和类内的差异。Erfani等人[57]提出了椭圆总结随机化（ESRand），它包括一个随机内核和椭圆数据总结。ESRand将每个领域投射到一个椭圆中以表示领域信息，然后使用一些相似性指标来计算距离。Hu等人[58]提出了多域判别分析法来对DG进行分类核学习，这种方法的粒度更细。Mahajan等人[74]提出使用因果匹配来学习分解表征，他们提出MatchDG来匹配在结果表征下相似的输入，以建立一个不变的分类器。对于领域泛化，一些基于核的方法的理论分析可以从[24, 26]中找到。

领域对抗性学习。领域对抗性训练被广泛用于学习领域不变的特征。Ganin和Lempitsky[77]和Ganin等人[78]提出了用于领域适应的领域对抗性神经网络（DANN），它对生成器和鉴别器进行对抗性训练。鉴别器被训练来区分领域，而生成器被训练来愚弄鉴别器以学习领域不变的特征表示。Li等人[64]对DG采用了这种想法。Gong等人[79]通过逐渐减少流形空间中的域差异来使用对抗性训练。Li等人[80]提出了一个条件不变的对抗网络（CIAN），用于学习DG的分类对抗网络。类似的想法也被用在[81, 85, 86]中。Jia等人[87]使用单边对抗学习和非对称三倍损失来确保只有来自不同领域的真实面孔是不可区分的，但对于假的面孔则不是。除了对抗性领域分类，Zhao等人[82]通过最小化不同训练领域的条件分布之间的KL分歧，引入了额外的熵正则化，以推动网络学习领域不变的特征。其他一些基于GAN的方法[45, 84, 27]也被提出，在理论上保证了泛化边界。

明确的特征对齐。这类工作通过明确的特征分布对齐[64, 128, 129]，或特征归一化[130, 131, 132, 62]，将各源域的特征进行对齐，以学习领域不变的表示。
Motiian等人[60]为表征学习引入了一个跨域对比性损失，其中映射的域在语义上是一致的，但又是最大限度的分离。一些方法通过最小化最大平均差异（MMD）[133, 127, 134, 135]、二阶相关[136, 137, 138]、均值和方差（时刻匹配）[129]、Wasserstein距离[128]等，明确地将特征分布分歧最小化，用于域适应或域概括。Zhou等人[128]通过最小化Wasserstein距离，通过最优传输将不同源域的边际分布对齐，实现域不变的特征空间。

此外，也有一些工作使用特征归一化技术来提高领域泛化能力[130, 131]。Pan等人[130]将实例归一化（IN）层引入CNN，以提高模型的泛化能力。IN在图像风格转换领域得到了广泛的研究[139, 140, 124]，图像的风格由IN参数反映，即每个特征通道的平均值和方差。因此，IN层[141]可用于消除特定实例的风格差异，以增强概括性[130]。然而，IN是与任务无关的，可能会消除一些鉴别性的信息。在IBNNet中，IN和批量归一化（BN）被平行利用，以保留一些鉴别性信息[130]。在[132]中，BN层被批量归一化（BIN）层所取代，它通过选择性地使用BN和IN来自适应平衡每个通道的BN和IN。Jin等人[62, 63]提出了一个风格归一化和恢复（SNR）模块，以同时确保网络的高泛化和辨别能力。在通过IN进行风格归一化后，进行还原步骤，从残差（即原始特征和风格归一化特征之间的差异）中提炼出与任务相关的鉴别特征，并将其添加到网络中以确保高鉴别力。恢复的想法被扩展到其他基于对齐的方法，以恢复因对齐而丢失的有用的鉴别性信息[142]。

不变风险最小化（IRM）。Arjovsky等人[88]从另一个角度考虑了领域泛化的表征的领域不变性。他们并不寻求与所有领域的表征分布相匹配，而是强制要求表征空间之上的最优分类器在所有领域都是一样的。其直觉是，预测的理想表征是y的原因，而因果机制不应受到其他因素/机制的影响，因此是领域不变的。

对 f 的约束体现了所有域共享相同的表示级分类器的愿望，而目标函数鼓励 f 和 g 实现低源域风险。然而，这个问题很难解决，因为它的约束条件中涉及到一个内部层次的优化问题。然后，作者开发了一个代用问题来学习特征提取器g，这个问题更加实用。

其中，一个假的表示级分类器f = 1被认为是，梯度规范项衡量这个分类器的最优性。这项工作还提出了一个可能是强线性假设下的泛化理论，即对于足够多的源域，可以确定基础真理不变的分类器。

由于新的概念和容易实现，IRM最近获得了明显的知名度。有一些关于IRM的成功[143]和失败案例的进一步理论分析[92]，而且IRM已经被扩展到其他任务，包括文本分类[91]和强化学习[144]。追求最优表示级分类器的不变性的想法也得到了扩展。Krueger等人[145]通过最小化源域之间的外推风险来促进这种不变性，这基本上是最小化源域风险的方差。Mitrovic等人[146]的目标是在自我监督的设置中学习这样的表征，其中第二域是通过显示各种语义不相关的变化的数据增量构建的。

1. 基于特征解缠的DG：解缠表征学习的目标是学习一个函数，该函数将样本映射到一个特征向量，该向量包含关于不同变化因素的所有信息，每个维度（或维度的一个子集）只包含关于某些因素的信息。基于Disentanglement的领域泛化方法一般将一个特征表示分解为可理解的组合/子特征，其中一个特征是领域共享/不变的特征，另一个是领域特定的特征。基于解缠的DG的优化目标可以总结为：

   $$min_{g_c,g_s,f} E_{x,y}l(f(g_c(x)), y) + \lambda l_{reg}+\mu l_{recon}([g_c(x),g_s(x)],x)$$

   其中 $gc$ 和 $g_s$ 分别表示领域共享和领域特定的特征表示。 λ，μ是权衡参数。损失 $l{reg} $是一个正则化项，明确鼓励领域共享特征和特定特征的分离，$l_{recon}$表示一个重建损失，防止信息的损失。注意，$[g_c (x), g_s (x)]$表示两种特征的组合/整合（不限于连接操作）。

   根据网络结构和实现机制的选择，基于解缠的DG方法主要可分为两类：多分量分析和生成模型。

   多组份分析。在多成分分析中，一般来说，使用领域共享和领域特定的网络参数来提取领域共享和领域特定的特征。UndoBias[94]的方法从SVM模型出发，在所有的训练数据上最大化区间分类，以实现领域泛化。他们将第 $i$ 个领域的参数表示为 $w_i = w_0 + ∆_i$，其中 $w_0$ 表示领域共享参数，$∆_i$表示领域特定参数。其他一些方法从不同方面扩展了UndoBias的思想。Niu等人[95]提出使用多视图学习进行领域泛化。他们提出了多视图DG（MVDG）来学习不同视图下的示范性SVM的组合，以实现稳健的泛化。Ding和Fu[96]为每个领域设计了特定领域的网络，并为所有领域设计了一个共享的领域变量网络，以学习不相干的表征，其中采用低秩重建的方式将两类网络以结构化的低秩方式对齐。Li等人[1]将UndoBias的思想扩展到神经网络背景下，并开发了一个用于端到端训练的低秩参数化CNN模型。Zunino等人[97]通过手动比较不同领域的某些区域的注意力热图来学习分解表征。还有其他一些作品采用多成分分析法进行解构[98, 93, 99, 100]。

   生成式模型。生成模型可用于从数据生成过程的角度进行拆分。这类方法试图从领域层面、样本层面和标签层面制定样本的生成机制。有些工作进一步将输入分解为与类别无关的特征，这些特征包含与特定实例相关的信息。Domain-invariant variational autoencoder (DIVA) [101]将特征分解为domain信息、类别信息和其他信息，这是在VAE框架下学习的。Peng等人[102]将细粒度的领域信息和类别信息进行了分解，这些信息在VAE中被学习。Qiao等人[39]也将VAE用于拆分，他们提出了一个统一特征拆分网络（UFDN），将感兴趣的数据域和图像属性都作为潜在因素来拆分。Liu等人[103]基于数据生成过程的因果观，提出了领域适应和领域泛化的统一解决方案，并为语义表示和泛化误差边界制定了一个识别保证。

学习策略

除了数据处理和表征学习，DG也被研究在一般的机器学习范式中，分为四类：基于集合学习的DG、基于元学习的DG、基于梯度运算的DG和其他。

1) 基于集合学习的通用技术：集合学习通常将多个模型（如分类器或专家）结合起来，以增强模型的力量。对于领域泛化，集合学习通过使用特定的网络架构设计和训练策略，利用多个源领域之间的关系来提高泛化能力。他们认为任何样本都可以被看作是多个源域的综合样本，因此整体预测结果可以看作是多个域网络的叠加。

Mancini等人[104]提出使用可学习的权重来汇总来自不同来源特定分类器的预测，其中一个领域预测器被用来预测样本属于每个领域的概率（权重）。Segu`等人[61]为不同的源域维护了与域相关的批判性归一化（BN）统计数据和BN参数，而所有其他参数是共享的。在推理中，最终的预测是依赖于域的模型的线性组合，其组合权重是通过测量测试样本的实例归一化统计数据和每个域的累积群体统计数据之间的距离推断出来的。105]的工作提出了不同源域的特定域层，并学习这些层的线性聚合来代表测试样本。Zhou等人[3]提出了领域自适应集合学习（DAEL），其中DAEL模型是由一个跨领域共享的CNN特征提取器和多个特定领域的分类器头组成。每个分类器对自己的领域来说是专家，对其他领域来说则是非专家。DAEL的目的是协同学习这些专家，通过对非专家的教学，鼓励集合体学习如何处理来自
未见过的领域的数据。

2) 基于元学习的DG：元学习的关键思想是通过基于优化的方法[147]或基于模型的方法[149]，从多个任务中学习通用模型。是通过基于优化的方法[147]、基于度量的学习[148]或基于模型的方法[149]，从多个任务中学习一个通用模型。元学习的思想已经被利用于领域概括。他们将多源领域的数据划分为元训练集和元测试集，以模拟领域转移。用θ表示要学习的模型参数，元学习可以表述为：

$$\begin{equation}\begin{split} \theta^* &= Learn(S_{mte};\phi^*) \\ &= Learn(S_{mte}; MetaLearn(S_{mtrn})) \end{split}\end{equation}$$

其中 $φ^*=MetaLearn(S{mtrn})$ 表示从元训练集 $S{mtrn}$ 中元学习的参数，然后用于在元测试集 $S_{mte}$ 上学习模型参数θ∗。这两个函数 Learn(-) 和 MetaLearn(-) 要由不同的元学习算法来设计和实现，这相当于一个双级优化问题。梯度更新可以表述为：

$$\theta = \theta - \alpha \frac{\partial(l(S_{mte};\theta) + \beta l(S_{mtrn}; \phi)) }{\partial \theta}$$

其中η,β分别是外循环和内循环的学习率。

Finn等人[147]提出了模型不可知元学习（MAML）。受MAML的启发，Li等人[12]提出了MLDG（meta-learning for domain generalization），将元学习策略用于DG。MLDG将源域的数据拆分为元训练和元测试，以模拟域转移的情况来学习一般的表征。Balaji等人[13]提出要为分类器学习元正则器（MetaReg）。[14]提出通过设计元优化器对特征提取器进行特征批评训练。Dou等人[108]使用了类似于MLDG的思想，另外还引入了两个互补的损失来明确规范化特征空间的语义结构。Du等人[15]提出了一个信息瓶颈的扩展版本，名为Meta Variational Information Bottleneck（MetaVIB）。他们对来自不同领域的具有相同类别的样本的潜在编码分布之间的Kullback-Leibler（KL）分歧进行正则化，并通过使用随机神经网络来学习生成权重。最近，一些作品也采用了元学习的方式来进行半监督式DG或判别式DG[109, 110, 111, 44]。

1. 基于梯度操作的DG：除了元学习和集合学习之外，最近的一些工作考虑使用梯度信息来迫使网络学习一般化的表征。Huang等人[112]提出了一种自我挑战的训练算法，旨在通过操纵梯度来学习一般表征。他们迭代地丢弃了在训练数据上激活的主导特征，并迫使网络激活与标签相关的剩余特征。通过这种方式，网络可以被迫从更多的坏情况中学习，这将提高泛化能力。Shi等人[113]提出了一个梯度匹配方案，他们的假设是两个领域的梯度方向应该是相同的，以增强共同表征学习。为此，他们提出将梯度内积（GIP）最大化，以调整各域的梯度方向。通过这种操作，网络可以找到权重，使输入-输出的对应关系在各领域中尽可能接近。GIP可以被表述为： $$L = L_{cls}(S_{train};\theta) - \lambda\frac{2}{M(M-1)} \sum_{i,j}^{i\neq j}G_i\cdot G_j$$ 其中 $G_i, G_j$ 是两个域的梯度，可以被 $G = E \frac{\partial l(x,y;\theta)}{\partial\theta}$ 计算得到

其他学习策略

还有一些其他的学习策略用于领域泛化。例如，自我监督学习是最近流行的一种学习范式，它从大规模的无标签数据中建立自我监督任务[150]。受此启发，Carlucci等人[114]引入了一个解决拼图的自我监督任务来学习泛化表征。
Li等人[116]交替地学习了特征提取器和分类器。首先，他们固定分类器来学习最坏情况下的特征提取器；然后，他们固定特征提取器来学习最坏情况下的分类器。通过这样的偶发训练，最终特征提取器和分类器可以从这些最坏情况中学习到更好的分布外任务的表现。Ryu等人[115]使用随机森林来提高卷积神经网络（CNN）的泛化能力。他们根据随机森林给出的拆分结果的概率质量函数对三联体进行采样，用于通过三联体损失更新CNN的参数。在未来，将有更多的工作用于使用其他学习策略的DG。

Future research challenges

总结了未来在领域泛化方面的一些研究挑战。

1）Continuous domain generalization 连续的领域泛化。在许多实际应用中，系统消耗的是具有非平稳统计数据的流媒体数据。在这种情况下，进行连续的领域泛化是非常重要的，它可以有效地更新DG模型以克服灾难性的遗忘并适应新的数据。虽然有一些专注于连续学习的领域适应方法[166]，但只有很少的关于连续DG的调查[167]，而这在实际场景中是有利的。

2）对新类别的领域泛化。现有的DG算法通常假定不同领域的标签空间是相同的。一个更实际、更普遍的设定是支持对新类别的泛化，也就是领域和任务的泛化。这在概念上类似于元学习和 zero-shot 学习的目标。一些工作[65,168]提出了 zero-shot DG，我们期望在这个领域有更多的工作。

3）可解释的领域概括。基于Disentanglement的DG方法将一个特征分解为领域不变/共享和领域特定的部分，为DG提供一些解释。对于其他类别的方法，目前仍然缺乏对DG模型中学习到的特征的语义或特征的深入理解。因果关系[103]可能是理解领域泛化网络并提供解释的一个有前途的工具。

4）大规模预训练/自学和DG：近年来，我们见证了大规模预训练/自学的快速发展，如BERT[169]、GPT- 3[170]和Wav2vec[171]。在大规模数据集上进行预训练，然后根据下游任务对模型进行微调，可以提高其性能，其中预训练有利于学习一般表征。因此，如何设计有用和高效的DG方法来帮助大规模的预训练/自我学习是值得研究的。

5）DG的性能评估：最近的工作[71]指出，在几个数据集上，一些DG方法的性能几乎与基线方法（即经验风险最小化）相同。我们不认为这就是DG在实际应用中没有用处的全部证据。相反，我们认为这可能是由于现在使用的评估方案不合适，或者是领域的差距没有那么大。在更现实的情况下，比如存在明显领域差距的人际关系[63]，DG的改进是巨大的。因此，我们对DG的价值保持肯定，并希望研究人员也能找到更合适的设置和数据集进行研究。