二分查找典型问题(二、三)

https://leetcode-cn.com/leetbook/read/learning-algorithms-with-leetcode/x4e1p5/

二、二分答案

二分答案意思是：题目要我们找的是一个整数，并且这个整数我们知道它可能的最小值和最大值。此时可以考虑用二分查找算法找到这个的目标值

69. Sqrt(x)

分析：这个题要求计算一个非负整数的平方根，返回值是一个整数。当平方根是浮点数事，需向下取整

法一：暴力解法

输入 8 返回的是 2 ， 因为 3 的平方等于 9 大于 8，因此【结果只保留整数的部分，小数部分将被舍去】。要求我们从1开始找，找到最后一个平方以后小于等于 x 的那个数。

假设 s 表示从 1 开始的那个数：

• 如果 s 平方以后小于 x， 暂时放过
• 如果 s 平方以后等于 x ，直接返回
• 如果 s 平方以后大于 x，说明 s-1 是题目要求，返回 s-1

public int mySqrt(int x) {
       // 特判
       if (x <= 1) {
           return x;
       }
       for (int i = 1; i <= x; ++i) {
           if (i == x / i) {
               return i;
           } else if (i > x / i) {
               return i - 1;
           }
       }
       throw new IllegalArgumentException("参数出错");
   }

注意：如果判别条件写成 s * s == x ，会发生整型溢出，应该写成 s = x / s ，判别条件 s * s > x 也是类似这样写。

复杂度分析：

时间复杂度：O(x)，最坏情况下暴力解法会一直尝试到 x/2，O(x/2)=O(x)；
空间复杂度：O(1)，只使用到常数个变量。

法二，二分查找

如果一个数的平方大于 x ，这个数就一定不是我们要找的平方根。于是，可以通过逼近的方式找到平方根。

public int mySqrt(int x) {
       if (x == 0) {
           return 0;
       }
       int left = 1;
       int right = x / 2;
       while (left < right){
           // 写完分支以后调整为向上取整
           int mid = (left + right + 1) / 2;     
           if (mid > x / mid) {
               // mid 以及大于 mid 的数一定不是解，下一轮搜索的区间为 [left, mid - 1]
               right = mid - 1;
           } else {
               left = mid;
           }
       }
       return left;
   }

287. 寻找重复数

• 要找 一个整数，这个整数有明确的范围 (1到n)之间，因此可以使用 二分查找。
• 每一次猜一个数，然后遍历整个数组，进而缩小搜索区间，然后确定重复的是哪个数。
• 不是在输入数组上直接使用二分查找，而是在数组 $[1,…,n]$ （有序数组）上使用二分查找。

理解题意：

• n + 1个整数，放在长度为 n 的数组里，根据抽屉原则，至少有一个数组重复
• 找重复，最容易想到的是哈希表
• 但题目要求，0(1)空间
• 找找一个有范围的整数可以用二分查找
• 快慢指针

二分查找的思路是先猜一个数（有效范围 $[left,…,right]$ 里位于中间的数 mid），然后统计原始数组中，小于等于mid 的元素个数cnt

• 如果cnt严格大于mid，根据抽屉原则，重复元素在 $[left, mid]$ 里
• 否则，重复元素就在 $[mid+1,..right]$

class Solution {
    public int findDuplicate(int[] nums) {
        int len = nums.length;

        int left = 0;
        int right = len - 1;
        while(left < right){
            int mid = left + (right - left) / 2;

            int cnt = 0;
            for(int num : nums){
                if(num <= mid){
                    cnt+=1;
                }
            }

            // 根据抽屉原理，小于等于4的个数如果严格大于4个，此时重复元素一定出现在 [1...4]里
            if(cnt > mid){
                right = mid;
            } else{
                left = mid + 1;
            }

        }
        return left;
    }
}

1300. 转变数组后最接近目标值的数组和

一句话解题：

• 使用二分法确定一个整数 threshold （就是提中说的value），使得这个 threshold下，【转变后的数组】的和最接近目标值 target
• 转变的规则是：严格大于threshold的元素变成 threshold，那么 threshold 越大，【转变后的数组】的和越大，这是单调性。（注意说得具体一点是：单调不减，因为有些情况下，阈值扩大后，和可能不变）

这道题比较麻烦的是求和以后可能不等于 target，所以让我们求【最接近的方案】，这个烦人的根源是 value 的取值一定得是整数，正是因为题目说 value 的整数，并且【答案不一定是arr中的数字】，因此依然可以使用二分查找法确定这个整数值。

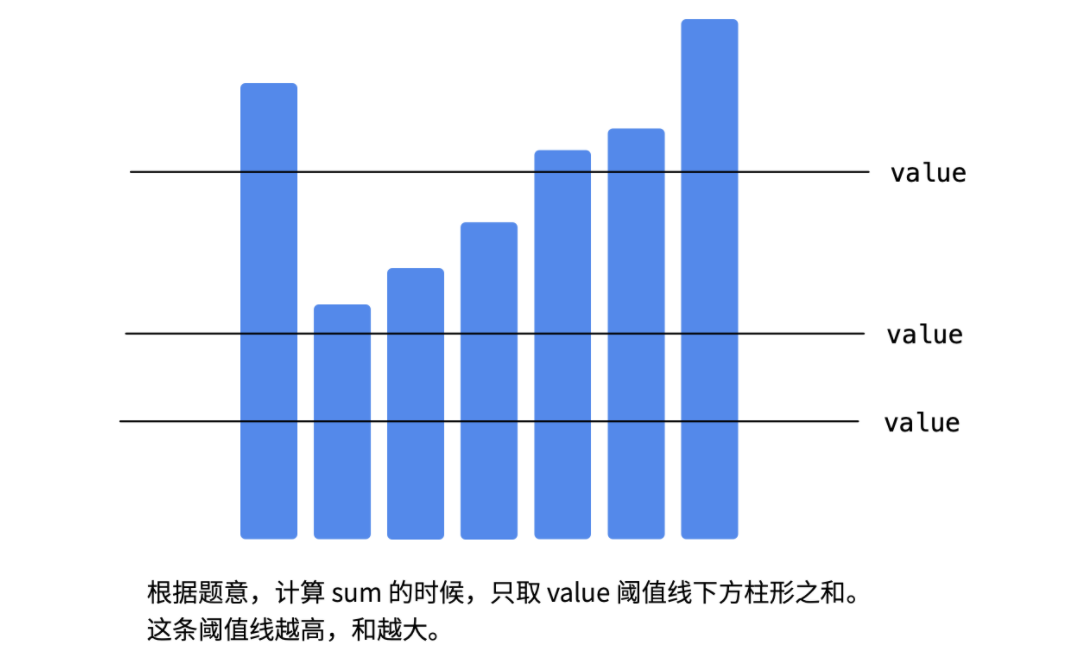
做题的时候，会发现判别条件很不好写，因为【怎么衡量接近】，度量这个【最接近】的量不好选，因为此需要考虑别的方案；

最接近的情况是：选定了一个value求和以后，恰恰好等于target。不过更有可能出现的情况是：value选得小了，接近程度变大，而value选得大了，接近程度变小。

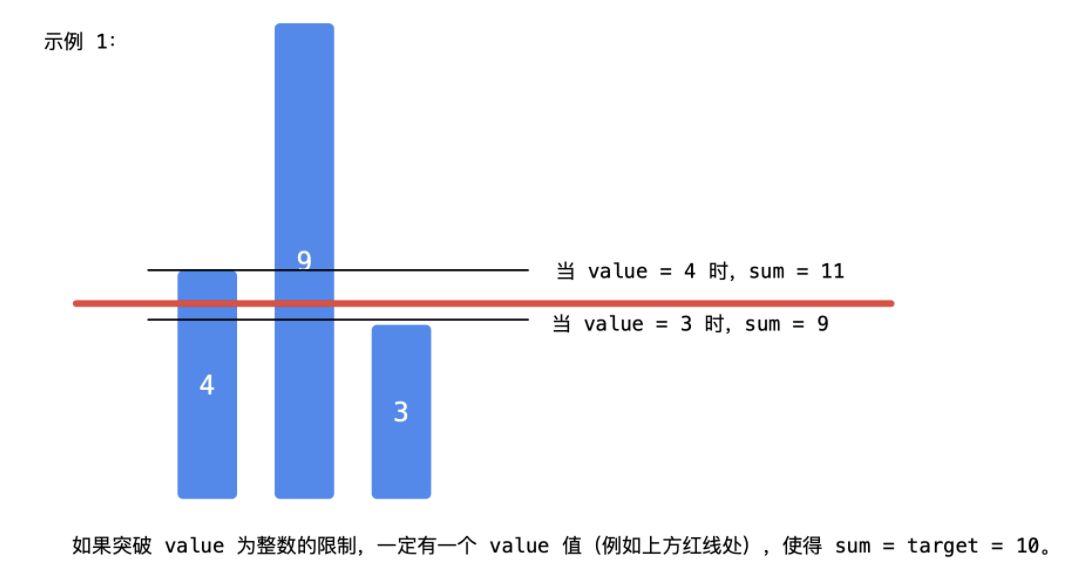
代码一

如果选择一个阈值 value，使得它对应的 sum 是第 1 个大于等于target的，那么目标值可能在 value 也可能在 value - 1

class Solution {
    public int findBestValue(int[] arr, int target) {
        int len=arr.length;
        int left = 0;
        int right = 0;

        for(int num: arr){
            right = Math.max(right, num);
        }

        while(left < right){
            int mid = left + (right - left) / 2;
            
            int sum = 0;
            for(int num : arr){
                sum += Math.min(num, mid);
            }
            // 计算第一个使得转变后数组的和大于等于target的阈值 threshold
            if(sum < target){
                // 严格小于的不一定是解
                left = mid + 1;
            }else{
                right = mid;
            }

        }

        // 比较阈值线分别定在 left-1 和left 的时候与target的接近程度
        int sum1 = 0;
        int sum2 = 0;
        for(int num:arr){
            sum1 += Math.min(num, left-1);
            sum2 += Math.min(num, left);
        }

        if(target - sum1 <= sum2 - target){
            return left - 1;
        }
        return left;
    }
  	/*
  	如果选择一个阈值 value ，使得它对应的 sum 是最后 1 个小于等于 target 的阈值，那么目标值可能在 value 也可能在 value + 1。
  	*/
  	public int findBestValue(int[] arr, int target) {
        int left = 0;
        int right = 0;
        // 注意：
        for (int num : arr) {
            right = Math.max(right, num);
        }

        while (left < right) {
            int mid = left + (right - left + 1) / 2;
            int sum = calculateSum(arr, mid);
            // 计算最后 1 个使得转变以后数组的和小于等于 target 的阈值 threshold
            if (sum > target) {
                // 大于等于的就不是解，threshold 太大了，下一轮搜索区间是 [left, mid - 1]
                right = mid - 1;
            } else {
                // 下一轮搜索区间是 [mid, right]
                left = mid;
            }
        }

        // 比较阈值线分别定在 left 和 left + 1 的时候与 target 的接近程度
        int sum1 = calculateSum(arr, left);
        int sum2 = calculateSum(arr, left + 1);
        // 注意：这里必须加绝对值，因为有可能出现 sum1 == sum2 < target 的情况
        if (Math.abs(target - sum1) <= Math.abs(sum2 - target)) {
            return left;
        }
        return left + 1;
    }

    private int calculateSum(int[] arr, int threshold) {
        int sum = 0;
        for (int num : arr) {
            sum += Math.min(num, threshold);
        }
        return sum;
    }
}

三、判别条件复杂的二分查找问题

在上一节【二分答案】中看到的问题是，根据目标变量具有的单调性质编写判别函数。

还有一类问题是这样的：目标变量和另一个变量有相关关系（一般而言是线性关系），目标变量的性质不好推测，但是另一个变量的性质相对容易推测。

这样的问题的判别函数通常会写成一个函数的形式。

875. 爱吃香蕉的珂珂

思路分析：

• 根据题意可以知道：珂珂吃香蕉的速度越小，耗时越多。反之，速度越大，耗时越小，这是题目的单调性
• 我们要找的速度，因为题目限制了一小时内只能选择一堆香蕉吃，因此速度最大值就是这几堆香蕉中，数量最多的那一堆。速度的最小值是1，其实还可以再分析一下下界是多少，由于二分搜素的时间复杂度很低，严格的Fenix不是很有必要。
• 还是因为一小时内只能选择一堆香蕉吃，因此：每堆香蕉吃完的耗时 = 这堆香蕉的数量/ 一小时吃香蕉的数量。根据题意，这里的 / 在不能整除的时候需向上取整

注意：当二分查找算法猜测的速度恰好使得珂珂在规定的实际内吃完香蕉的时候，还应该去尝试更小的速度是不是还可以保证在规定的时间内吃完香蕉

class Solution {
    public int minEatingSpeed(int[] piles, int h) {
        int n = piles.length;

        int maxVal = 1;
        for(int pile: piles){
            maxVal = Math.max(maxVal, pile);
        }

        // 速度最小的时候，耗时最长
        int left = 1;
        // 速度最大的时候，耗时最短
        int right = maxVal;

        while(left < right){
            int mid = left + (right - left) / 2;
            if(calculateSum(piles, mid) > h){
                //耗时太多，说明速度太慢，下一轮搜索区间是 [mid+1, right]
                left = mid +1;
            }else{
                right = mid;
            }
        }
        return left;
    }

    private int calculateSum(int[] piles, int speed){
        int sum=0;
        for(int pile : piles){
            // 向上取整可以这样写
            sum += (pile + speed -1) / speed;
            // 还可以这样
            // if (pile % speed == 0){
            //     sum += pile / speed;
            // }else{
            //     sum += pile / speed + 1;
            // }
        }
        return sum;
    }
}

时间复杂度：

• 时间复杂度： $O(Nlog \ max(piles))$, 这里 N 表示数组 piles 的长度、我们在 $[1,max\ piles]$ 里使用二分查找，定位最小速度，而每一次执行判别函数的时间复杂度是 $O(N)$

410. 分割数组的最大值

• 动态规划的写法其实是穷举：按照长度、前缀、枚举最后一个划分，记录每一步结果。细节比较多，需要作图+仔细讨论边界情况，并且属性二维数组、三层for循环的写法；
• 本题的二分查找思路：查找一个有范围的整数，关于在利用单调性逼近这个整数。

题意分析：各自和的最大值最小：

• 由于数组是确定的，其中一组得分多，相应的另一组分到的值就少，所以对于任意一种拆分（切成 m 段），这 m 段可以取最大值 val
• 需要找一种拆分，使得这个最大值 val 的值是所有分成 m 段拆分里值最小的那个；

方法1：动态规划

枚举所有的分割情况，例如题目中的输入数组【7，2，5，10，8】分割成两个非空连续子数组，可以有以下四种方式：

• [7, | 2, 5, 10, 8]；
• [7, 2, | 5, 10, 8]；
• [7, 2, 5, | 10, 8]；
• [7, 2, 5, 10, | 8]。

比较容易想到的递归结构是：

• 找到最后一个分割，求出这个分割的连续子数组的和，与之前的分割取最大值。
• 枚举最后一个分割，找出所有最大值中最小的那一个

整个过程稍微有一些繁琐，但是思想是直接的：对于所有长度的 前缀区间（题目中的关键信息是子数组连续，所以考虑前缀区间），枚举所有可能的分割，并记录每一步的结果，递推完成计算。以题目中的示例 [7, 2, 5, 10, 8] 为例：

先考虑 所有前缀区间 分割成 1 个非空连续子数组的情况：

• [7] 分割成 1 个非空连续子数组的和，就是整个数组的和 7，下同；
• [7, 2] 分割成 1 个非空连续子数组的和，就是整个数组的和 9；
• [7, 2, 5] 分割成 1 个非空连续子数组的和，就是整个数组的和 14；
• [7, 2, 5, 10] 分割成 1 个非空连续子数组的和，就是整个数组的和 24；
• [7, 2, 5, 10, 8] 分割成 1 个非空连续子数组的和，就是整个数组的和 32；

再考虑 所有前缀区间 分割成 2 个非空连续子数组的情况：

• [7] 不能分割成 2 个非空连续子数组的和；
• [7, 2] 分割成 2 个非空连续子数组，只有 1 种分割情况：[7, | 2] ，其中「[7] 分割成 1 个非空连续子数组」的情况我们在第 1 步计算过；
• [7, 2, 8] 分割成 2 个非空连续子数组，有 2 种分割情况：
• [7, | 2, 8] ，其中「[7] 分割成 1 个非空连续子数组」的情况我们在第 1 步计算过；
• [7, 2, | 8] ，其中「[7, 2] 分割成 1 个非空连续子数组」的情况我们在第 2 步计算过；

分析到这里，可以把递推结构形式化描述成如下：

第一步：定义状态

$dp[i][k]$ 表示：将前缀区间 $[0, i]$ 被分成 k 段的各自和的最大值的最小值记为 $dp[i][k]$，那么前缀区间 $[0, j]$ （这里 j < i） 被分成 k - 1 段各自和的最大值的最小值为 $dp[j][k - 1]$。

即：第一维是第 k 个分割的最后一个元素的下标 i ，第二维是分割的总数 i。

第二步：推导状态转移方程

$$dp[i][k] = max(dp[j][k-1],rangeSum(j+1,i))$$

这里 $rangeSum(j + 1, i)$ 表示数组 $nums[j + 1..i] $的区间和，它可以先计算出所有前缀和，然后以 O(1) 的方式计算出区间和。

上面的状态转移方程中，j 的值需要枚举。我们画图分析：

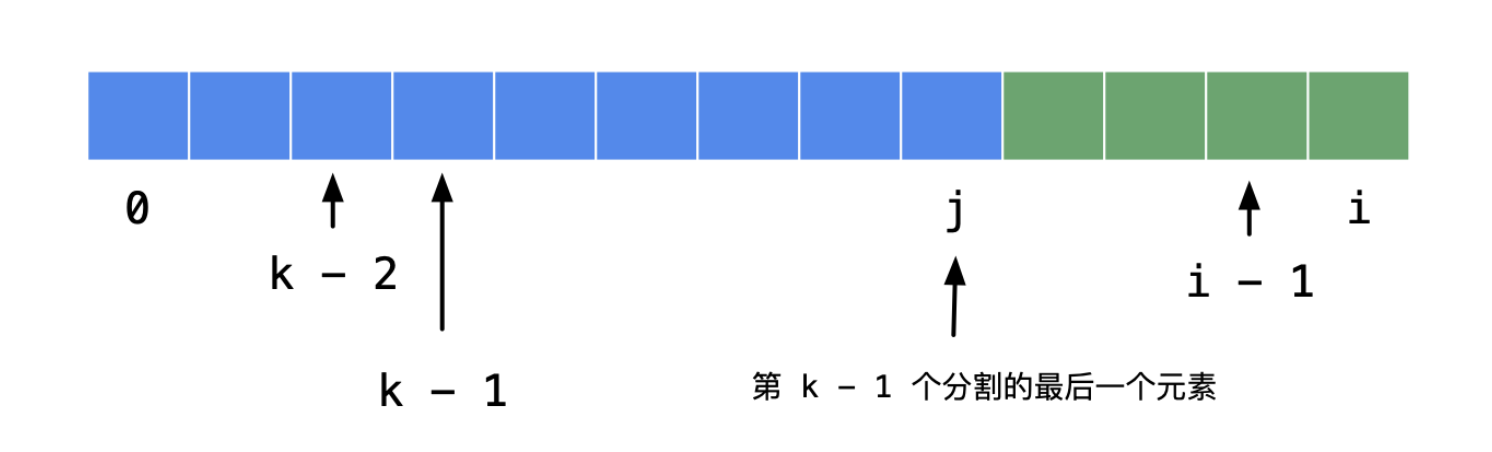
• 由于区间 [0, j] 一定要分成 k - 1 个非空连续子数组；
• j 的意义是：第 k - 1 个分割的最后一个元素的下标；
• 而下标 k - 1 的前面（不包括 k - 1），一共有 k - 1 个元素（这一条只要是下标从 0 开始均成立）；
• 故 j 的枚举从 k - 2 开始，到 i - 1 结束，因为第 k 个分割至少要有 1 个元素。

第三步：思考初始化

• 由于要找最小值，初值赋值成为一个不可能达到的很大的值；
• 分割数为 1 ，即不分割的情况，所有的前缀和就是依次的状态值。

第 4 步：思考输出

$dp[len][k]$，根据状态定义，这是显然的。

下面给出题目中的示例 [7, 2, 5, 10, 8] 的状态计算表，为了更突出一般性，把 m 设置成为数组的长度 5：

编码的思考路径：

我们按照阶段、状态和选择进行分析，依次把三层循环写下来：

• 阶段：依次计算长度为 1 的区间、长度为 2 的区间，直到题目要求的长度为 m 的区间；
• 状态：前缀区间 [0, i] 的状态值，由于 i 要被分成 k 份，前缀区间里至少要有 k 个元素，最小前缀区间 k 个元素的最后一个元素的下标为 k - 1，故 i 从 k - 1 开始到 len - 1；
• 选择：枚举第 k - 1 个分割的最后一个元素的下标，根据上面的分析，从 k - 2 到 i - 1。

方法2：二分查找

题目关键字：【非负整数数组】和【连续】这两个信息

与69题、287题：可以用于查找一个有范围的整数，就能想到是不是可以使用二分查找去解决

挖掘单调性：使用二分查找的一个前提是【数组具有单调性】，我们就去想想有没有单调性可以挖掘，不难发现：

• 如果设置【数组各自和的最大值】很大，那么必然导致分割数很小
• 如果设置【数组各自和的最大值】很小，那么必然导致分割数很大

可以通过调整【数组各自和的最大值】来达到：使得分割数恰好为 m 的效果。这里要注意一个问题：

如果某个数组各自的最大值恰好使得分割数为 m，此时不能放弃搜索，因为我们要使得这个最大值 最小化，此时还应该继续尝试缩小这个数组各自和的最大值，使得分割数超过 m，超过 m 的最后一个使得分割数为 m 的数组各自和的最大值就是我们要找的最小值。

举个例子：

例如：（题目中给出的示例）输入数组为【7，2，5，10，8】，m=2。如果设置数组各自和的最大值为 21那么每个的是【7，2，5，|10，8】，此时 m = 2，此时这个值太大，尝试一点一点缩小：

• 设置 数组各自和的最大值 为 20，此时分割依然是 [7, 2, 5, | 10, 8]，m = 2；
• 设置 数组各自和的最大值 为 19，此时分割依然是 [7, 2, 5, | 10, 8]，m = 2；
• 设置 数组各自和的最大值 为 18，此时分割依然是 [7, 2, 5, | 10, 8]，m = 2；
• 设置 数组各自和的最大值 为 17，此时分割就变成了 [7, 2, 5, | 10, | 8]，这时 m = 3。

m 变成 3 之前的值 数组各自和的最大值 18 是这个问题的最小值，所以输出 18。

class Solution {
    public int splitArray(int[] nums, int m) {
        int max = 0;
        int sum = 0;

         // 计算「子数组各自的和的最大值」的上下界
        for(int num :nums){
            max = Math.max(max, num);
            sum += num;
        }

        // 使用【二分查找】确定一个恰当的【子数组各自的和的最大值】
        int left = max;
        int right = sum;
        while(left < right){
            int mid = left + (right - left) / 2;

            int splits = split(nums, mid);
            if(splits > m){
                // 如果分割数太多，说明【子数组各自的和的最大值】太小，此时需要将【子数组各自的和的最大值】调大
                // 下一轮搜索的区间是【mid+1，right】
                left = mid+1;
            }else{
                right = mid;
            }
        }
        return left;

    }

    private int split(int[] nums, int maxIntervalSum){
        // 至少是一个分割
        int splits = 1;
        // 当前区间的和
        int curIntervalSum = 0;
        for(int num : nums){
            // 尝试加上当前遍历的这个数，如果加上去超过了【子数组各自的和的最大值】，就不加这个数，另起炉灶
            if (curIntervalSum + num > maxIntervalSum){
                curIntervalSum = 0;
                splits++;
            }
            curIntervalSum += num;
        }
        return splits;
    }
}

1011. 在 D 天内送达包裹的能力

对于左边界而言，由于我们不能「拆分」一个包裹，因此船的运载能力不能小于所有包裹中最重的那个的重量，即左边界为数组 weights 中元素的最大值。

对于右边界而言，船的运载能力也不会大于所有包裹的重量之和，即右边界为数组 weights 中元素的和。

class Solution {
    public int shipWithinDays(int[] weights, int days) {
        
        int maxVal = 0;
        int sum = 0;
        for(int w : weights){
            maxVal = Math.max(maxVal, w);
            sum+=w;
        }

        int left = maxVal;
        int right = sum;
        // int left = Arrays.stream(weights).max().getAsInt(), right = Arrays.stream(weights).sum();

        while(left < right){
            int mid = left + (right - left) / 2;

            int cur = cal(weights, mid);
            if (cur <= days) {
                right = mid;
            } else {
                left = mid + 1;
            }

        }
        return left;

    }
    private int cal(int[] weights, int mid){
        int need = 1, cur = 0;
        for (int weight : weights) {
            if (cur + weight > mid) {
                ++need;
                cur = 0;
            }
            cur += weight;
        }
        return need;
    }
}

1482. 制作 m 束花所需的最少天数

class Solution {
    public int minDays(int[] bloomDay, int m, int k) {

        int len = bloomDay.length;

        if(m * k > len){
            return -1;
        }

        int maxVal = 0;
        int minVal = 0;
        for(int b : bloomDay){
            maxVal = Math.max(b, maxVal);
            minVal = Math.min(b, minVal);
        }

        int left = minVal;
        int right = maxVal;

        while(left < right){
            int mid = left + (right - left) / 2;

            int cur = cal(bloomDay ,mid, m, k);
            if(cur >= m){
                right = mid;
            }else{
                left = mid + 1;
            }
        }
        return left;

    }


    private int cal(int[] bloomDay, int mid, int m, int k){
        int curNum = 0;
        int f = 0;
        for(int b:bloomDay){
            if(b <= mid){
                f++;
                if(f==k){
                    curNum++;
                    f=0;
                }
            }else{
                f=0;
            }
        }
        return curNum;
    }
}

LCP 12. 小张刷题计划

class Solution {
    public int minTime(int[] time, int m) {
        if(time.length < m){
            return 0;
        }

        int left = 0;
        int right = Integer.MAX_VALUE;

        while(left < right){
            int mid = left + (right - left) / 2;

            if(check(time, m, mid)){
                right = mid;
            }else{
                left = mid + 1;
            }
            
        }
        return left;
    }

    public boolean check(int[] time, int m, int limit){
        int cur = 0, sum = 0, max = 0, day = 1; // 当前遍历的题目，当前组的总耗时，当前组的最大耗时，需要的天数
        while(cur < time.length){
            sum += time[cur];
            max = Math.max(max, time[cur]);
            if(sum - max > limit){// 当前组总耗时减去组内最大耗时仍超出限制，则需开启额外一天
                day ++;
                if(day > m){// 超出总天数m，无法完成分配
                    return false;
                }
                sum = time[cur]; // sum和max更新为新组的值
                max = time[cur];
            }
            cur++;
        }
        return true; // 能遍历完所有题目即完成了分配
    }
}