Parameter-Efficient Transfer Learning with Diff Pruning
Parameter-Efficient Transfer Learning with Diff Pruning
Diff pruning 使参数有效的迁移学习在新任务中得到良好的扩展。
该方法学习了一个特定于任务的 “diff “向量,该向量对原始预训练的参数进行了调整。在训练过程中,这个 diff 向量通过对L0-norm惩罚的可微调近似来适应性地修剪,以鼓励稀疏性。
随着任务数量的增加,diff pruning仍然具有参数有效,因为它只需要为每个任务存储一个小的diff向量。由于它不需要在训练期间访问所有任务,因此它在任务以流形式设置中很有吸引力。
在GLUE基准测试中,diff pruning可以与微调基线的性能相媲美,而每个任务只需修改0.5%的预训练模型参数,与流行的修剪方法相比,其扩展性更强。
Introduction
针对特定任务对预训练的深度网络进行微调是当代NLP的主流模式,在一系列自然语言理解任务中取得了最先进的结果。
虽然这种方法简单明了,在经验上也很有效,但很难扩展到多任务、内存受限的情况下(例如设备上的应用),因为它需要为每个任务运送和存储一整套模型参数。
由于这些模型是通过自监督的预训练来学习可推广的、与任务无关的语言表征,因此为每个任务微调整个模型似乎特别浪费。
提高参数有效的一种流行方法:
- 《Compressing BERT: Studying the Effects of Weight Pruning on Transfer Learning》
- 《Poor Man’s BERT: Smaller and Faster Transformer Models》
- 《Masking as an Efficient Alternative to Finetuning for Pretrained Language Models》
- 《Adaptive Sparsity by Fine-Tuning》
是为每个任务学习较小的压缩模型。这种方法面临着严重的稀疏性/性能权衡,并在每个任务中保留大量非零参数(例如10%-30%)。多任务学习和基于特征的迁移允许每个任务进行更有效的参数迁移学习。
多任务学习和 feature-based 的迁移允许每个任务的参数效率更高的迁移学习:
- 《Multi-Task Deep Neural Networks for Natural Language Understanding》
- 《BAM! Born-Again Multi-Task Networks for Natural Language Understanding》
- 《BERT and PALs: Projected attention layers for efficient adaptation in multi-task learning》
- 《Sentence- BERT: Sentence Embeddings using Siamese BERT-Networks》
这些方法在共享模型的基础上训练少量附加参数(例如线性层)。然而,多任务学习通常需要在训练期间访问所有任务,以防止灾难性遗忘,而 feature-based 的迁移学习(例如,基于任务不可知的句子表示)通常通过微调表现得更好
一个有吸引力的中间地带是为特定任务 finetune 基础模型的扩展。这种方法在保持基于特征的转移的任务模块化的同时,还能抓住 finetune 的训练优势。
例如,Adapters 使用较小的特定任务模块,在模型的层之间插入这种方法不需要在训练期间访问所有的任务,针对现实环境,随着新的任务流到达(
《Parameter-efficient transfer learning for nlp》
《Adapter- Fusion: Non-Destructive Task Composition for Transfer Learning》
)发现,适配器层可以在GLUE基准上匹配完全微调的BERT的性能,而每个任务需要3.6%的额外参数(平均)。
Diff pruning 是对预训练模型的一个新的扩展,目的是为了更参数有效的迁移学习。Diff pruning 不是修改模型的结构,而是通过一个特定任务的 diff 向量扩展基础模型。
为了学习这个向量,我们将特定任务的模型参数重新参数化为 $θ{task} = θ{pretrained} + δ{task}$,其中预训练的参数向量 $θ{pretrained}$是固定的,特定任务的 diff 向量 $δ_{task}$ 是微调的。差异向量用L0-norm惩罚的可微调近似值进行重构,以鼓励稀疏性。
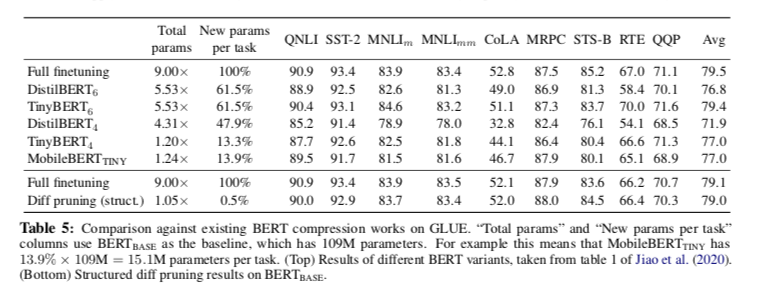
Diff pruning 可以变得非常有效的参数,因为它只需要为每个任务存储 diff 向量的非零位置和权重。存储共享预训练模型的成本保持不变,并在多个任务中分摊。在GLUE基准上,Diff pruning 可以匹配完全微调的BERT基线的性能,而每个任务只微调0.5%的预训练参数。随着任务数量的增加,diff pruning在所需的存储量方面优于流行的基于剪枝的方法。
Background: Transfer Learning
NLP中的迁移学习大多使用 pretrain finetune 范式,它从预训练的模型中为所有任务初始化一个模型参数子集,然后根据特定的任务目标进行调整。预训练目标包括上下文预测、自动编码、机器翻译,以及最近的语言建模的变种目标。
这里我们考虑将转移学习应用于多个任务。 我们考虑的是具有潜在的未知任务集(可能以流的形式到达)的设置,其中每个任务 $τ∈T$ 有一个相关的训练集 $D{\tau} = {x{\tau}^{(n)}, y{\tau}^{(n)}}{n=1}^{N}$。对于所有任务,目标是产生(可能是捆绑的)模型参数 $θ_τ$,使经验风险最小化,
其中,$fτ(\cdot;θτ)$ 是一个关于输入的参数化函数(例如神经网络),$C(\cdot,\cdot)$是一个损失函数(例如交叉熵)1,R(-)是一个具有超参数 $λ$ 的操作性正则器。
我们可以通过简单地学习每个任务的独立参数来使用 pretrain finetune 方法。然而,预训练模型的巨大规模使得这种方法的参数非常不方便。例如,广泛采用的模型,如BERT-BASE 和 BERT-LARGE,分别有1.1亿和3.4亿个参数,而他们同代的模型有数十亿的参数数。 解决这种参数效率低下的经典方法是通过联合训练,针对多个任务训练一个共享模型(连同特定任务的输出层)。然而,多任务学习的通常表述要求事先知道任务集 $T$,以防止灾难性的遗忘,这使得它不适合于任务集未知或任务流到来的应用。
Diff Pruning
Diff pruning 将特定任务的微调表述为学习一个 diff 向量 $δ_τ$,该向量被添加到预先训练的模型参数 $θ$ 中,该参数保持固定。我们首先对特定任务的模型参数进行重新参数化,
这导致了下面的经验风险最小化问题,
为了简洁起见,我们将 $L(Dτ, fτ, θ_τ)$ 定义为:
这种微不足道的重新参数化表明,存储预训练参数 $θ$ 的成本在不同的任务中被分摊,而新任务的唯一边际成本是 diff向量。如果我们能将 $δ$ 正则化,使其稀疏,从而使 $||\delta_{\tau}||_0 << ||\theta||_0$,那么随着任务数量的增加,这种方法可以变得更具有参数效率。我们可以用差值向量的L0-norm惩罚来指定这一目标,
Differentiable approximation to the L0-norm
这个正则器很难优化,因为它是不可微分的。为了近似这个L0目标,我们采用了一种基于梯度的学习方法,即使用一个宽松的掩码向量进行L0稀疏度学习《Learning Sparse Neural Networks through L0 Regularization》
这种方法包括将 binary vector 放宽到连续空间,然后与密集的权重向量相乘,以确定在训练中应用多少权重向量。训练结束后,掩码被制成确定性的,并且很大一部分 diff 向量为零。
为了应用这种方法,我们首先将 $δ_τ$ 分解成一个二进制掩码向量,再乘以一个密集向量。
我们现在对真实目标进行下限,并对关于 $zτ$ 的期望进行优化,其分布 $p(zτ; ατ)$ 初始是伯努利,并引入参数 $ατ$。
这个目标仍然因为 $z_τ$ 的离散性而变得复杂,但是这个期望为经验上有效松弛提供了一些指导。
遵循先前的工作《Learning Sparse Neural Networks through L0 Regularization》,将 $zτ$ 放宽到连续空间 $[0, 1]^d$,并采用拉伸的 Hard-Concrete 分布,这样就可以使用路径梯度估计器。具体来说,$zτ$ 现在被定义为来自均匀分布的样本 $u$ 的一个确定性和(次)可微函数。
这里 $l<0, r>1$是两个常数,用来将 $s_τ$ 拉伸到区间 $(l,r)^d$,然后用 $min(1, max(0, \cdot))$ 操作将它夹在 $[0, 1]^d$中。在这种情况下,我们有一个预期L0-norm的可微闭式表达。
因此,最终的优化问题由以下方式给出,
为了减少符号的混乱,我们把没有经过预训练的特定任务输出层的参数归入θ。我们现在可以利用路径梯度估计器来优化关于 $ατ$ 的第一项,因为期望不再依赖于它。 训练后,我们通过对 $u$ 采样一次以获得 $zτ$(即 不一定是二进制向量,但由于钳位函数的原因,其维数非常多,恰好为零),然后设置 $δτ = zτ \odot w_τ $
L0-ball projection with magnitude pruning for sparsity control
微分 L0 正则化使我们能够实现高稀疏率。然而,最理想的是设置一个精确的稀疏率,特别是考虑到需要参数预算的应用。由于正则化系数 $λ$ 是某个 $η$ 的约束条件 $E[||δ_τ||_0]< η$ 的拉格朗日乘数,原则上可以通过搜索不同的 $λ$ 值来实现。 然而,我们发现通过训练后投影到目标 L0-ball 上实现精确的稀疏率更有效率,而且经验上也更有效。
《Structured Pruning of Large Language Models》
具体来说,我们对 diff 向量 $δτ$ 使用 magnitude pruning 幅度修剪,通过在 $δτ$ 中只保留前 $t \%\times d$ 的值来达到稀疏率 $t\%$。注意,与标准的 magnitude pruning 不同,这是基于diff向量值的幅度而不是模型参数。我们发现,在固定非零掩码的情况下进一步微调 $δ_τ$ 以保持良好的性能是很重要的,这也是 magnitude pruning 中经常出现的情况。由于这种通过投射到L0-ball 上的参数效率可以在没有自适应 diff puning的情况下应用,这样的方法将作为我们在实证研究中的基线之一。
Structured Diff Pruning
为了使diff pruning能够适应模型结构,我们考虑了一个结构化的扩展,其中包括维度之间的依赖性。假设,这种方法可以让模型学会在局部区域修改参数,而不是独立处理每个参数。修改正则器,首先将参数索引分为G组 $ {g(1),…,g(G)}$,其中 $g(j)$ 是由组 $g(j)$ 支配的参数指数的子集。
然后,为每个组 $g(j)$ 引入一个标量 $z^jτ$(及相关参数 $α^jτ$),并将索引 $i\in g(j)$的特定任务参数分解为 $δj = z{τ,i} - z^jτ - w{τ,i}$
然后,期望的L0范数由下式给出:
我们可以像以前一样用基于梯度的优化训练。一个组中的参数被正则器所鼓励,共同被移除。
Experiments
Model and datasets
为了评估,使用GLUE基准以及SQuAD抽取式问题回答数据集。按照Adapters,在GLUE任务的以下子集上测试。
- 多类型自然语言推理(MNLI),目标是预测两个句子之间的关系是包含关系、矛盾关系还是中性关系(我们在 $MNLIm$ 和 $MNLI{mm}$上进行测试,分别对匹配/不匹配的领域进行测试);
- Quora问题对(QQP),一个分类任务,预测两个问题是否语义等同;
- 问题自然语言推理(QNLI),必须预测一个句子是否是问题的正确答案。
- Stanford Sentiment Treebank (SST-2),一个预测电影评论情绪的句子分类任务;
- Corpus of Linguistic Acceptability (CoLA),其目标是预测一个句子在语言上是否可以接受。
- 语义文本相似性基准(STS-B),必须预测两个句子之间的相似性等级;
- 微软研究院转述语料库(MRPC),目标是预测两个句子是否在语义上等同;
- 识别文本关联(RTE),必须预测第二个句子是否被第一个句子所包含。
该基准对CoLA使用Matthew’s correlation,对STS-B使用Spearman,对MRPC/QQP使用F1 score,对MNLI/QNLI/SST- 2/RTE使用accuracy。
Baselines
将结构化和非结构化的 diff pruning 变体与以下基线进行比较:
- Full finetuning:像往常一样对BERT-LARGE进行完全微调
- Last layer finetuning:仅微调倒数第二层(连同最终输出层)
- Adapters:该研究在预训练模型的每一层之间训练特定任务的瓶颈层,通过改变瓶颈层的大小,可以对参数效率进行控制。
- Non-adaptive diff pruning:在magnitude pruning的基础上进行diff pruning(即,通过通常的微调获得$\theta{\tau}$,设置 $\delta{\tau} = \theta{\tau} - \theta$,然后应用magnitude pruning,再对 $\delta{\tau}$ 进行额外的微调)。对于diff pruning,我们将目标稀疏率设置为0.5%
Structured vs. Non-structured Diff Pruning

结构化Diff Pruning 为每个组引入了一个额外的掩码,这鼓励了对整个组进行 pruning。这比传统的组稀疏技术的限制性要小,这些技术被用于L0-norm松弛,迫使一个组中的所有参数共享同一个掩码。然而,我们仍然期望整个组更经常地被pruning 掉,这可能会使学习过程偏向于完全消除或将非零 diff 聚在一起。在表3中,我们确实发现,结构化的差异修剪导致的微调模型更有可能使整个组与它们的预训练值(零差异)没有变化。
Task-specific Sparsity
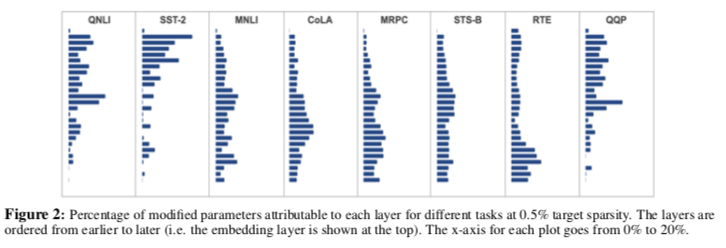
预训练模型的不同层被认为是对不同信息的编码。鉴于每个任务可能会招募不同种类的语言现象嵌入到隐藏层中,我们假设 diff pruning 将通过特定任务的微调来修改预训练模型的不同部分。图2显示了每个任务中不同层的非零 diff 参数的百分比。我们发现,不同的任务确实修改了网络的不同部分,尽管有些任务之间存在一些质量上的相似性,例如QNLI和QQP(都必须对问题进行编码),以及MRPC和STS-B(都必须预测句子间的相似性)。嵌入层对所有任务的修改都很稀疏。虽然稀疏性分布的一些变化是由于简单的随机性造成的,但我们确实观察到在同一任务的多次运行中存在一定程度的一致性。
Effect of L0-ball projection
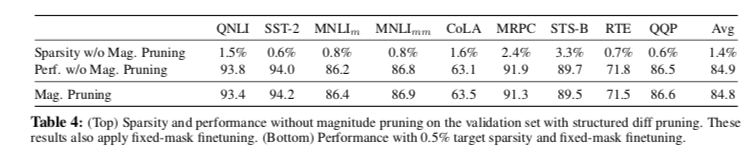
应用 magnitude pruning 幅度修剪来投影到L0-ball上是实现精确稀疏目标的关键。如表4所示,我们观察到通过此方法在性能上几乎没有损失。我们重申,使用固定掩码进行微调至关重要,即使对于不应用幅度修剪的方法也是如此。