Adapting BERT for Continual Learning of a Sequence of Aspect Sentiment Classification Tasks

增量学习ASC任务序列的CL系统应解决以下两个问题：

将从以前的任务中学到的知识转移到新的任务中，帮助它学习更好的模型
维护以前任务的模型性能，以便不会忘记它们

针对这些问题，本文提出了一种新的基于胶囊网络的模型B-CL (BERT-based Continual Learning) ，受《Parameter-efficient transfer learning for NLP》的Adapter Bert启发。

B-CL通过前向和后向知识转移显著提高了ASC在新任务和旧任务上的效果。

ASC任务定义如下：给定一个方面(例如，相机评论中的图像质量)和在特定领域(例如，相机)中包含该方面的意义，分类句子对该方面表示正面、负面还是中性(无意见)。

利用胶囊和动态路由来识别与新任务相似的先前任务，并利用它们的共享知识来帮助新任务学习，并使用任务掩码来保护任务特定的知识，以避免遗忘(CF)。

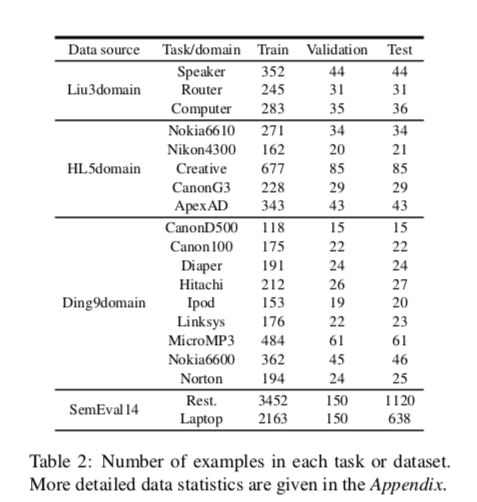
Adapter-BERT

一个 adapter 是具有残差连接的2层全连接网络。只有adapter(黄框)和layer norm(绿色框)层是可训练的。其他模块(灰色框)被冻结。提出的的B-CL，用CLA代替适配器。CLA有两个子模块：知识共享模块(KSM)和任务特定模块(TSM)

在结束任务的训练期间，只训练适配器和规格化层，不改变任何其他BERT参数，这对CL是好的，因为微调BERT本身会导致严重的遗忘。

Capsule Network

与CNN不同的是，CapsNet用矢量胶囊取代了标量特征检测器，可以保留图像中的位置和厚度等额外信息。典型的CapsNet有两层胶囊层。

初级图层存储低级特征映射，类别层生成分类概率，每个胶囊对应一个类。它使用动态路由算法使每个较低级别的封装能够将其输出发送到类似的(或“agreed”，由点积计算的)较高级别封装。这是用来识别和分组相似任务及其共享功能或知识的关键属性。

值得注意的是，所提出的B-CL不采用整个胶囊网络，因为只对胶囊层和动态路由感兴趣，而对最大边际损失和分类器不感兴趣。

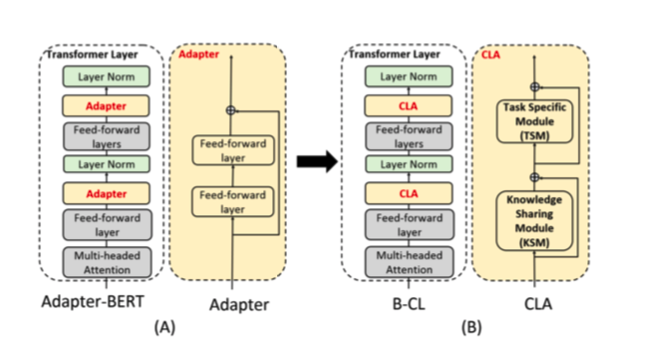
Continual Learning Adapter (CLA)

B-CL的目标是：

通过知识共享实现相关旧任务与新任务之间的知识转移；
通过防止新任务学习覆盖先前任务的特定任务知识来获得回避。

CLA的体系结构如图所示

知识共享模块(KSM)，用于从相似的先前任务和新任务中识别和利用可共享的知识
任务特定模块(TSM)，用于学习任务特定神经元并保护它们不被新任务更新。

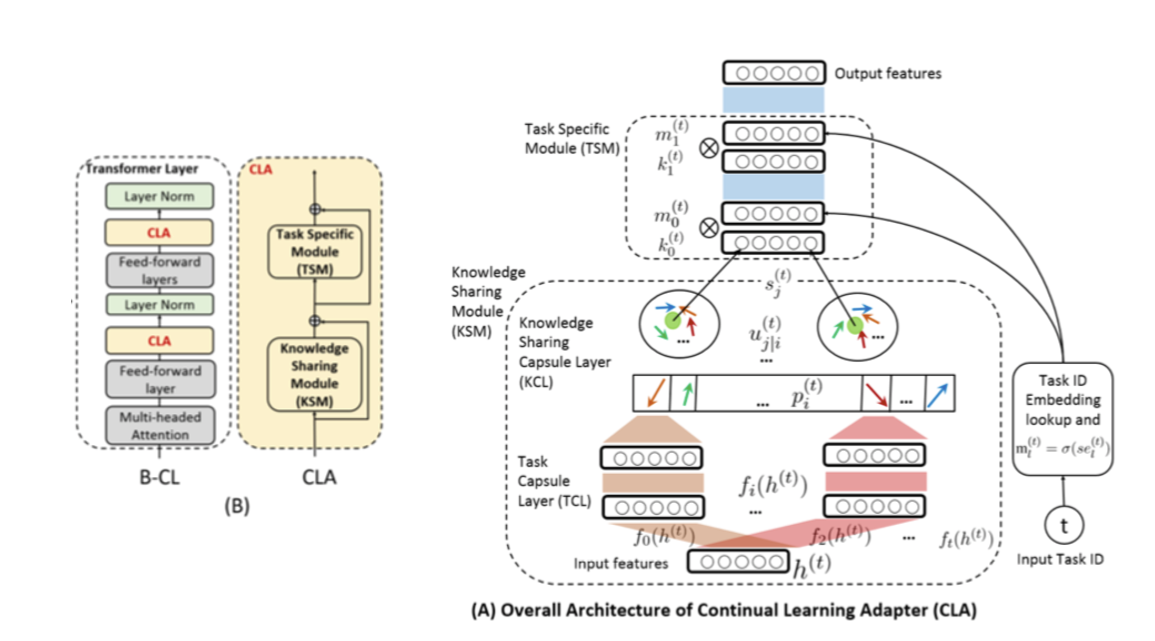
CLA接受两个input：

来自transformer层内部前馈层的隐藏状态 $h^{(t)}$
task ID $t$

output是隐藏状态，具有适合第t个任务的特征。

KSM 利用胶囊层（见下文）和动态路由对相似的任务和可共享的知识进行分组，

而 TSM 利用任务掩码 (TM) 来保护特定任务的神经元并让其他神经元自由。这些自由的神经元稍后被TSM用于一项新的任务。由于TM是可微的，所以整个系统B-CL可以被端到端地训练。下面将详细介绍每个模块。

KSM 将相似的任务和共享的知识（特征）分组到它们之间，以实现相似任务之间的知识转移。这是通过两个胶囊层（任务胶囊层和知识共享胶囊层）和胶囊网络的动态路由算法实现的。

Task Capsule Layer (TCL)

TCL中的每个胶囊代表一个任务，TCL准备从每个任务派生低级特征。因此，对于每个新任务，TCL都会添加一个胶囊。

这种增量生长是有效且容易的，因为这些胶囊是离散的并且不共享参数。而且，每个胶囊只是一个具有少量参数的2层完全连接的网络。

$h^{(t)} \in R^{d_t\times d_e}$ 为CLA的输入，$d_t$ 是tokens数量，$d_e$是维度。

令到目前为止学习的任务集为 $T{prev}$（在学习新任务 t 之前）和 $|T{prev}|= n$

在 TCL 中，我们有 n+1 个不同的胶囊代表所有过去的 n 个学习任务以及新任务 t。

第 $i(i≤n+1)$ 个任务的封装为:

$p_i^{(t)} = f_i (h^{(t)})$

其中 $f_i(\cdot) = MLP_i(\cdot)$ 代表为2层全连接层。

KCL 中的每个知识共享胶囊都捕获那些具有相似特征或共享知识的任务（即它们的任务胶囊 ${p_i^{(t)}}_1^{n+1}$ ）。

这是通过动态路由算法自动实现的。召回动态路由鼓励每个较低级别的胶囊（在案例中为任务胶囊）将其输出发送到类似（或“agreed”）的更高级别的胶囊（在我们的案例中为知识共享胶囊）。

本质上，相似的任务胶囊（具有许多共享特征）通过较高的系数（决定任务胶囊可以进入下一层的程度）“聚集”在一起，而不同的任务（具有很少的共享特征）则通过低系数。

这种聚类识别来自多个任务封装的共享特征或知识，并且有助于在相似任务之间向后转移。

KCL首先将每个任务胶囊 $pi^{(t)}$ 变成临时特征 $u{j|i}^{(t)}$：

$u_{j|i}^{(t)} = W_{ij} p_i^{(t)}$

临时特征与权重 $c^{(t)}_{ij}$ 相加以获得知识共享胶囊 $s^{(t)}_j$ 中的初始值：

$s_j^{(t)} = \sum_i c_{ij}^{(t)} u_{j|i}^{(t)}$

其中 $c{ij}^{(t)}$ 是耦合系数加和为1。请注意，方程 1 中每个任务的任务胶囊映射到方程 3 中的知识共享胶囊，$c{ij}^{(t)}$ 表示第 i 个任务的表示对第 j 个知识共享胶囊的信息量。

因此，知识共享胶囊可以表示不同的可共享知识。这确保仅使用与新任务显着或相似的任务胶囊，而忽略（并因此保护）其他任务胶囊以学习更一般的可共享知识。

在反向传播时，用较小梯度更新具有低 $c^{(t)}{ij }$ 的相异任务，然而相似的任务有较高的$c^{(t)}{ij }$被更新较大的梯度。这鼓励在类似任务之间向后转移。

Dynamic Routing

$c_{ij}^{(t )}$ 是由“Routing Softmax”计算的：

$c_{ij}^{(t)} = \frac{exp(b_{ij}^{(t)})}{ \sum_o exp(b_{io}^{(t)})}$

其中每个 $b_{ij}$ 是对数先验概率，显示任务胶囊 $i$ 与知识共享胶囊 $j$ 的显著性或相似性。

它被初始化为0，表示它们之间在开始时没有显著联系。应用动态路由算法来更新 $b_{ij}$：

$b_{ij}^{(t)} \leftarrow b_{ij}^{(t)} + a_{ij}^{(t)}$

其中 $a{ij}$ 是协议系数，直观上，这一步倾向于聚合知识共享胶囊上的相似（或“agreed”）任务，具有更高的一致性系数 $a{ij}^{(t)}$，因此具有更高的 logit $b^{(t)}{ij}$ 或耦合系数 $c{ij}^{(t )}$ 。协议系数的计算公式为 :

$a_{ij}^{(t)} = u_{j|i} ^{(t)} \cdot v_{j}^{(t)}$

其中 $v_{j}^{(t)}$ 是规范化的表示形式，通过非线性 squash

$v_{j}^{(t)} = \frac{ ||s_j^{(t)}||^2 }{1+||s^{(t)}_j||} \frac{s_j^{(t)}}{||s_j^{(t)}||}$

对于第一个任务 $sj^{(t)} = u{j|i}^{(t)} $ , 其中 $v^{(t)}_{j}$ 归一化为[0，1]到表示知识共享胶囊 j 的激活概率。

Task Specific Module (TSM)

虽然知识共享对ASC很重要，但为以前的任务保存特定于任务的知识以防止遗忘(CF)也同样重要。

为此，使用任务掩码。具体地说，首先检测每个旧任务使用的神经元，然后在学习新任务时关闭或屏蔽所有使用过的神经元。

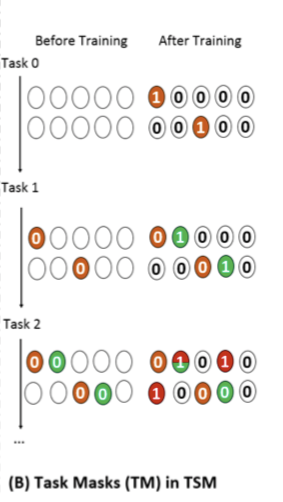
每项任务的两行对应于TSM中的 $k^{(t)}_0$ 和 $k^{(t)}_1$。在训练前的细胞中，0的细胞是需要保护(掩蔽)的神经元，那些没有编号的细胞是游离的神经元(未使用)。

在学习第一个任务（任务 0）后，获得了用橙色标记的有用神经元，每个神经元中都标有 1，作为学习未来任务的掩码。在学习任务 1 中，那些对任务 0 有用的神经元被屏蔽（左侧的橙色神经元或细胞中的 0 为 0）。该过程还学习了任务 1 的有用神经元，用 1 标记为绿色。当任务 2 到达时，任务 0 和 1 的所有重要神经元都被屏蔽，即其掩码条目设置为 0（训练前的橙色和绿色）。在训练任务 2 之后，我们看到任务 2 和任务 1 有一个对它们都很重要的共享神经元。共享神经元以红色和绿色标记。

在训练后的细胞中，那些带有1的细胞显示了对当前任务重要的神经元，这些神经元被用作未来的mask。具有一种以上颜色的单元格表示它们由多个任务共享。这0个没有颜色的单元格不会被任何任务使用。