Meta-Learning Representations for Continual Learning

持续学习的代理应该能够在现有知识的基础上快速学习新数据，同时最大限度地减少遗忘。

目前基于神经网络函数逼近器的智能系统 很容易遗忘，而且很少经过训练来促进未来的学习。这种糟糕行为的一个原因是，他们从没有为这两个目标明确训练的表征中学习。

本文提出了OML，它的目标是通过学习表征来直接最小化灾难性的干扰，加速未来的学习，并且在连续学习中对在线更新下的遗忘具有健壮性。

证明了学习自然稀疏表示是可能的，这对于在线更新更有效。此外，该算法是对现有的连续学习策略(如MER和GEM)的补充。

有经验的程序员学习一门新的编程语言比以前从未编程的人要快得多，而且不需要忘记旧的语言来学习新的语言。

在这项工作中，显式地学习一种持续学习的表示法，以避免干扰并促进未来的学习。设计一个元目标，它使用灾难性干扰作为训练信号，通过在线更新直接优化。目标是学习一种表示，以便模型在 meta-test 时使用的随机在线更新总体上提高其预测的准确性。

Problem Formulation

Continual Learning Prediction (CLP)问题由无休止的样本流组成

$$T = (X_1,Y_1) ,(X_2,Y_2) ,..., (X_t,Y_t) ...$$

随机向量 $Yt$ 根据未知分布 $p(Y|X_t)$抽样。我们假设过程 $X_1,X_2,..,X_t,…$有一个边际分布 $\mu ：X \to [0,\infty)$，它反映了每个输入被观察到的频率。这种假设允许各种相关序列。例如，可以从潜在依赖于过去变量 $X{t-1}$ 和 $X_{t-2}$ 的分布中采样 $X_t$。然而目标 $Y_t$ 仅依赖于 $X_t$ , 而不依赖于过去的 $X_i$。

定义 $Sk = (X{j+1}, Y{j+1}),(X{j+2}, Y{j+2}) ,…,(X{j+k}, Y_{j+k}) $ 为从CLP问题 $T$ 中抽样的长度为 $k$ 的随机轨迹。

最后，$p(S_k|T)$ 给出了可以从问题 $T$ 中抽样的所有长度为 $k$ 的轨迹上的分布。

对于给定的CLP问题，我们的目标是学习一个函数 $f_{W,\theta}$ 它可以预测给定 $X_t$ 的 $Y_t$。更具体地说，设 $l:Y\times Y \to R$ 是将预测 $\hat y \in Y$ 和目标 $y$ 之间的损失定义为 $l(\hat y,y)$的函数。

如果假设输入 $X$ 与某个密度 $\mu$ 成正比： $X \to [0,\infty)$, 那么我们希望最小化目标：

$$L_{CLP}(W,\theta) = E[l(f_{W,\theta}(X), Y)] = \int \left[ \int l(f_{W,\theta}(x), y) p(y|x) dy \right] \mu(x) dx$$

其中 $W,\theta$ 代表一系列参数，是更新和最小化的目标。

为了最小化 $L_{CLP}$，我们将自己限制在通过从 $p(S_k|T)$ 采样的单个 $k$ 长度轨迹上的在线更新来学习。

这改变了标准 iid 设置中的学习问题——模型看到长度为 k 的相关样本的单一轨迹，而不是直接从 $p(x, y) = p(y|x)\mu(x)$ 中采样。当简单地为IID设置应用标准算法时，此修改可能会引起重大问题。相反，我们需要设计考虑这种相关性的算法。

这个公式可以表示各种连续问题。 一个例子是在线回归问题，例如在给定当前位置的情况下预测机器人的下一个空间位置； 另一个是现有的增量分类基准。 CLP 公式还允许依赖于最近 m 次观测的历史记录的目标 $Yt$。 这可以通过将每个 $X_t$ 定义为最后 m 个观测值来获得。 $X_t$ 和 $X{t-1}$ 之间的重叠不违反对相关输入序列的假设。 最后，强化学习中的预测问题——从一个状态预测策略的值——可以通过将输入 $X_t$ 视为状态和要采样的目标返回或引导目标来表示。

Method

端到端训练的神经网络在使用从 $p(S_k|T)$ 采样的单个轨迹来最小化CLP loss 方面不是有效的，原因有两个。

首先，它们的样本效率极低，需要多个epoch的训练才能收敛到合理的解决方案。

其次，当在线学习相关数据流时，他们会受到灾难性的干扰。

元学习可以有效地提高神经网络的样本效率。但元学习模型初始化，这种归纳偏差不足以解决灾难性的干扰问题。

经验发现，学习编码器比只学习初始化的性能要好得多，此外，元学习优化问题在学习编码器时表现更好(对超参数不敏感，收敛速度更快)。这种差异的一种解释是，当在高度相关的数据流上学习时，全局且贪婪的更新算法(例如梯度下降)将贪婪地改变神经网络的初始层相对于当前样本的权重。初始层中的这种变化将干扰模型的过去知识。因此，初始化不是增量学习的有效归纳偏差。另一方面，当学习编码器 $\phi_{\theta}$ 时，神经网络可以学习使得更新不那么全局的高度稀疏表示(因为连接到零的特征的权重保持不变)。

为了将神经网络应用于问题的求解，作者提出了一种元学习函数 $\phi_{\theta} (X)$ ——一种由 θ 参数化的深度表示学习网络(RLN)—从$X \to R^{d}$中学习。然后学习另一个来自 $R^d\to Y$的函数 $g_W$，称为预测学习网络(PLN)。

两个函数的组合为 $f{W,\theta }(x) = g{W}(\phi_{\theta} (X))$

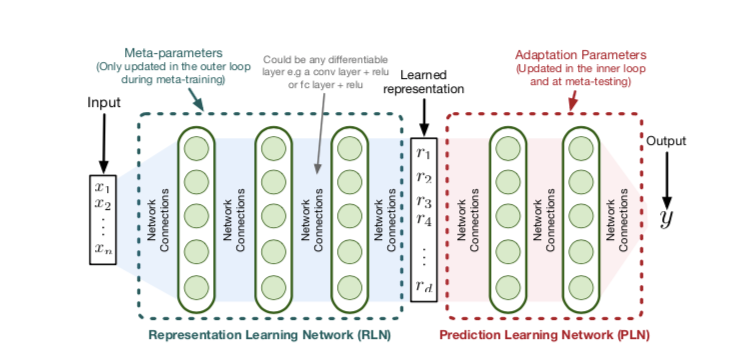
将 $\theta$ 视为通过最小化元目标学习的元参数，然后在元测试时固定。在学习 $\theta $ 之后，我们从 $R^d\to Y $ 学习 $g_W $，用于从单个轨迹 $S $ 使用单次传递全在线的SGD更新解决CLP问题。

对于元训练，假设由 $p(T)$ 给出的CLP问题上的分布。

OML的目标函数为 ：

$$min_{W,\theta} \sum_{T_i \sim p(T)} OML(W,\theta) = \sum_{T_i\sim P(T)} \sum_{S_k^j\sim p(S_k|T_i)} [ L_{CLP_i} (U(W,\theta, S_k^j))]$$

其中 $Sk^j = (X{j+1}^i,Y{j+1}^i),(X{j+2}^i, Y{j+2}^i),…,(X{j+k}^i,Y_{j+k}^i)$ ,

$U(Wt, \theta, S_k^j) =(W{t+k},\theta)$ 表示一个更新 $W_{t+k}$ 是k步SGD后的权重向量

U 中第 $j$ 步更新 在样本 $(X{t+j}^i, Y{t+j}^i)$ 使用参数 $W{t+j-1}, \theta$ , 得到 $(W{t+j},\theta)$

MAML-Rep和OML目标可以分别实现为算法1和算法2，两者之间的主要区别以蓝色突出显示:

注意，MAML-Rep使用完整批数据 $S_k$ 进行 $l$ 次内部更新(其中 $l $ 是超参数)，而OML使用 $S_k$ 中的一个数据点进行一次更新。这使得OML可以考虑在线持续学习的影响，例如灾难性的遗忘。

OML 目标的目的是学习适合在线持续学习的表示。 为了说明什么将构成持续学习的有效表示，假设我们有三个输入集群，它们具有显着不同的 $p(Y |x)$，对应于 $p1$、$p_2$ 和 $p_3$。 对于固定的二维表示 $\phi{\theta} : X \to R^2$，我们可以考虑由线性模型给出的解 $W\in R^2$ 的线性模型，该模型为每个 $p_i$ 提供等效准确的解。

这三个过程在图2中的 $W\in R^2$参数空间中描述为三条不同颜色的线。

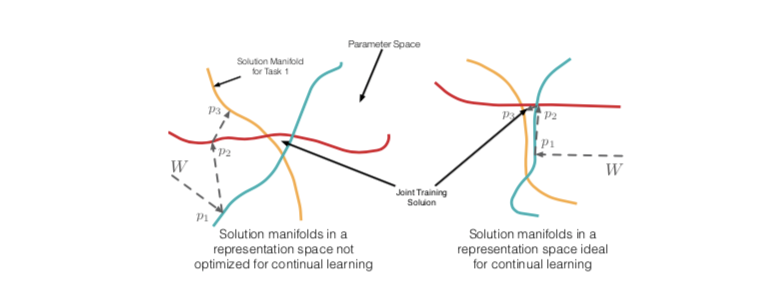
对于目标是由三个不同的分布 $p_1(Y|x)$ 、$p_2(Y|x)$ 和 $p_3(Y|x)$生成的问题，研究了表示对连续学习的影响。

目的是通过对来自三个分布的样本进行在线学习，找到一个对所有三个分布都有效的参数向量 W。 对于两种不同的表示，这些流形及其交集可能看起来非常不同。 直觉是，当流形平行（允许正泛化）或正交（避免干扰）时，来自 W 的在线更新更有效。 产生这种流形的表示不太可能自然出现。 相反，我们必须明确地找到它。 通过考虑在线持续学习的影响，OML 目标针对这种表示进行了优化。