Efficient lifelong learning with A-GEM

从样本复杂度、计算和内存成本方面研究了当前终身学习方法的效率。

首先引入了一个新的、更现实的评估协议，学习者只观察每个例子一次，超参数选择是在一个小的、不相交的任务集上完成的，不用于实际的学习体验和评估 .

其次，引入了一个新的度量标准来衡量学习者获得一项新技能的速度。

第三，提出了 GEM 的改进版本，称为平均 GEM (A-GEM)，它具有与 GEM 相同甚至更好的性能，同时在计算和内存效率方面几乎与 EWC 和其他基于正则化的方法一样。

最后，包括A-GEM在内的所有算法，如果提供指定所考虑的分类任务的任务描述符，则可以更快地学习。

Learning protocol

一种新的学习范式，即学习者对一组与实际用于评估的任务集不相交的任务进行交叉验证。在这种情况下，学习者将必须学习并将在一个全新的任务序列上进行测试，并且它将仅在该数据流上执行一次。

以前关于终身学习的工作采用直接从监督学习中借用的学习范式。 有 T 个任务，每个任务由训练集、验证集和测试集组成。 在训练期间，学习者根据需要对每个任务的数据进行尽可能多的传递。

此外，通过根据交叉验证网格搜索所需的次数扫描整个任务序列来调整验证集上的超参数。最后，使用由先前交叉验证过程选择的模型在每个任务的测试集上报告度量。

由于当前范式违反了我们对 LLL 的更严格定义，即学习者只能对数据进行一次传递，因为我们想强调从数据中快速学习的重要性，因此现在引入了一种新的学习范式。

我们考虑由以下有序数据集序列描述的两个任务流：

$D^{CV}={D1,…,D{T^{CV}}}$ 和 $D^{EV} = {D_{T^{CV}+1},…,D_T}$

其中 $Dk = {(x_i^k,t_i^k,y_i^k){i=1}^{n_k}}$ 是第k个任务的数据集。 $T^{CV}<T$ 在实验中 $T^{CV}=3,T=20$

我们假设所有数据集都来自相同的任务分布。 为了避免符号混乱，让上下文指定 $D_k$ 是指第 k 个数据集的训练集或测试集。

$D^{CV}$是交叉验证期间将使用的数据集的流。$D^{CV}$允许学习者出于模型超参数选择的目的多次重放所有样本。

相反，$D^{EV}$是用于测试集的最终训练和评估的实际数据集。学习者将观察 $D^{EV}$ 中的训练样本一次且仅一次，并且所有指标都将在 $D^{EV}$的测试集上报告。

Metrics

引入了一个新的度量标准来衡量学习速度，它有助于量化一个学习算法学习一个新任务的能力—— Learning Curve Area (LCA)

每个任务的训练数据集 $D_k$ 由总共 $B_k$个小批次组成。在每次呈现一小批任务 $k$ 之后，使用相应的测试集来评估学习者在所有任务上的表现。

设 $\alpha_{k,i,j}\in [0,1]$是用任务 $k$ 的第 $i$ 个小批次训练模型后，在任务 $j$ 的测试集上评估的准确度。

假设连续体中的第一个学习任务由1索引 ( $T^{CV}+1$ 对应于 $D^{EV}$ ) , $T$ 的最后一个(对于 $D^{CV}$ ，将是 $T^{CV}$)，我们定义了以下指标：

Average Accuracy

$A\in [0,1]$ 用所有小批量连续训练模型后的平均精度，直到任务k被定义为：

$$A_k = \frac{1}{k} \sum_{j=1}^k \alpha_{k, B_{k},j}$$

$A_T$ 是所有任务的平均准确率，是最后一个任务学习后得到的。这是LLL中最常用的度量。

Forgetting Measure

$F \in [-1,1]$ 模型经过所有小批量连续训练后的平均遗忘，直到任务 k 被定义为：

$$F_k = \frac{1}{k-1} \sum_{j=1}^{k-1} f_j^k$$

其中 $f_j^k$ 是在使用所有小批量训练模型直到任务 k 并计算为：

$$f_j^k = max_{l\in \{1,...,k-1\}} \alpha_{l,B_l,j} - \alpha_{k, B_k, j}$$

在学习完所有任务后测量遗忘很重要，原因有两个。它量化了过去任务的准确率下降，并给出了模型学习新任务的速度的间接概念，因为健忘的模型几乎没有剩余的知识可以转移，特别是如果新任务与其中一个任务更密切相关 。

Learning Curve Area

$LCA \in [0,1]$ 让我们首先定义模型在所有 T 任务训练后的平均 b-shot 性能（其中 b 是小批量数）：

$$Z_b = \frac{1}{T} \sum_{k=1}^T \alpha_{k,b,k}$$

$\beta$ 处的 LCA 是作为 $b \in [0, \beta]$ 函数的收敛曲线 $Z_b$ 的面积：

$$LCA_{beta} = \frac{1}{\beta+1} \int_0^{\beta} Z_b db = \frac{1}{\beta+1} \sum_{b=0}^{\beta} Z_b$$

LCA 有一个直观的解释。 $LCA0$ 是平均 0-shot 表现，与 GEM 中的前向转移相同。 $LCA{\beta}$ 是 $Zb$ 曲线下的区域，如果 0-shot 性能好并且学习器学习速度快，则该区域很高。 特别是，可能有两个模型具有相同的 $Z_b$ 或 $A_T$ ，但 $LCA{\beta}$ 非常不同，因为一个模型比另一个学习得快得多，而它们最终都获得了相同的最终精度。 该度量旨在区分这两种情况，并且对于相对较小的 $\beta$ 值是有意义的，因为我们对从少数示例中学习的模型感兴趣。

Averaged gradient episodic memory (A-GEM)

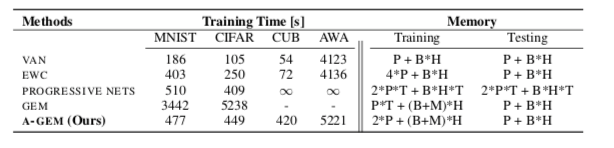
A-GEM 建立在 GEM 的基础上，该算法利用小的情节记忆在单遍设置中表现良好，并对损失函数提出了一个小的改变，使 GEM 在 训练时间，同时保持相似的表现；

回顾GEM

GEM在计算和内存成本方面很高。GEM通过为每个任务 $k$ 存储情节记忆 $M_k$ 来避免灾难性遗忘。

在最小化当前任务 t 的损失的同时，GEM 将任务 k<t 的情景记忆的损失视为不等式约束，避免其增加但允许其减少。

$$l (f_{\theta}, M_k) = \frac{1}{|M_k|} \sum_{(x_i,k,y_i)\in M_k} l(f_{\theta}(x_i,k),y_i)$$

这有效地允许 GEM 进行其他 LLL 方法不支持的 积极反向迁移。 形式上，在任务 t，GEM 解决以下目标：

$$minimize_{\theta} \ \ l (f_{\theta}, D_t) \ \ s.t. \ \ l(f_{\theta}^{t-1}, M_k) \ \ \ \ \forall k<t$$

其中 $f_{\theta}^{t-1}$ 是训练到任务 $t−1$ 的网络，为了检查损失的增加，GEM 计算先前任务的损失梯度 $g_k$ 向量与当前任务 $g$ 的梯度更新之间的角度。只要与任何 $g_k$ 的角度大于 90°，它就会将建议的梯度投影到 L2 范数梯度 $\hat g$ 中最接近的，从而使角度保持在边界内。 形式上，GEM 解决的优化问题由下式给出：

$$minimize_{\hat g} \ \ \frac{1}{2}||g-\hat g||_2^2 \ \ \ s.t. \ \ <\hat g,g_k> \ge0 \ \ \ \forall k<t$$

这是一个 凸优化中二次规划的问题， P 变量（网络中的参数数量）中的二次规划 (QP)，对于神经网络而言，可能是数百万。为了有效地解决这个问题，GEM 在对偶空间中工作，这导致只有 t − 1 个变量的更小的 QP：

$$minimize_v \ \ \frac{1}{2}v^TGG^Tv + g^TG^Tv \ \ s.t. \ \ v\ge0$$

其中 $G = -(g1,…,g{t-1}) \in R^{(t-1)\times P}$ 是在训练的每个梯度步骤计算的。一旦上式找到最优解 $v^{}$， 投影梯度可以计算为：$\hat g =G^Tv^{} + g$

虽然 GEM 已被证明在单个 epoch 设置中非常有效，但性能提升的前提是训练时的计算负担很大。在每个训练步骤中，GEM使用情景记忆中的所有样本来计算矩阵 $G$ ，并且它还需要求解QP。当M的大小和任务数量很大时，此内循环优化变得令人望而却步。

A-GEM

GEM 确保在每个训练步骤中，每个单独的先前任务的损失（由情景记忆中的样本近似）不会增加

而 A-GEM 试图确保在每个训练步骤中，先前任务的平均情景记忆损失不会增加。 形式上，在学习任务 t 时，A-GEM 的目标是：

$$minimize_{\theta} \ \ \ l(f_{\theta}, D_t) \ \ \ s.t. \ \ l(f_{\theta}, M) \le l (f_{\theta}^{t-1}, M) \ \ where \ M =\cup_{k<t} M_{k}$$

相应的优化问题简化为：

$$minimize_{\hat g} \ \ \frac{1}{2}||g-\hat g||_2^2 \ \ s.t. \ \ \hat g^Tg_{ref} \ge 0$$

其中 $g{ref}$ 是使用从情节记忆 $(x{ref},y_{ref}) \sim M$ 中随机采样的批次计算得出的梯度。

换句话说，A-GEM 用单个约束替换了 GEM 的 t-1 约束，其中 $g_{ref}$ 是从情景记忆的随机子集计算出的先前任务的梯度的平均值。

现在可以非常快速地解决上面方程的约束优化问题； 当梯度 g 违反约束时，它通过以下方式进行投影：

$$\hat g = g- \frac{g^Tg_{ref}}{g^{T}_{ref}g_{ref}} g_{ref}$$

这使得 A-GEM 不仅内存高效，因为它不需要存储矩阵 G，而且比 GEM 快几个数量级，因为

• 1）不需要计算矩阵 G 而只需要计算内存样本的随机子集的梯度

• 2）它不需要解决任何 QP，只需要解决一个内积

• 3）它会产生更少的违背约束，特别是当任务数量很大时。

  所有这些因素一起使 A-GEM 更快，同时不会妨碍其在单程设置中的良好性能。

证明推导 A-GEM update rule

给出了A-GEM更新规则 $\hat g = g- \frac{g^Tg{ref}}{g^{T}{ref}g{ref}} g{ref}$ 的证明

A-GEM的优化目标:

$$minimize_{\hat g} \ \ \frac{1}{2}||g-\hat g||_2^2 \ \ s.t. \ \ \hat g^Tg_{ref} \ge 0$$

将 $\hat g$ 替换为 $z$，并重写：

$$minimize_{\hat g} \ \ \frac{1}{2} z^z -g^z \ \ s.t. \ -z^Tg_{ref}\le 0$$

请注意，目标中丢弃了项 $g^Tg$，并更改了不等式约束的符号。 上面定义的约束优化问题的拉格朗日可以写成：

$$L(z,\alpha) = \frac{1}{2} z^Tz - g^z - \alpha z^Tg_{ref}$$

方程的对偶：

$$\theta_D(\alpha) = min_z L(z,\alpha)$$

通过将 $L(z, \alpha)$ 相对于 z 的导数设置为零来找到最小化 $L(z, \alpha)$ 的值 $z^∗$：

$$\nabla_z L(z,\alpha) = 0 \ ,\ z^* = g+\alpha g_{ref}$$

代入 $z^∗$ 值后的简化对偶:

$$\theta_D(\alpha) = \frac{1}{2} (g^Tg +2\alpha g^Tg_{ref} +\alpha^2 g^Tg_{ref} ) - g^Tg-2\alpha g^Tg_{ref} - \alpha^2g_{ref}^Tg_{ref} \\ = -\frac{1}{2}g^Tg - \alpha g^Tg_{ref} - \frac{1}{2}^2g_{ref}^Tg_{ref}$$

对偶的解 $\alpha^* = max{\alpha;\alpha>0} \theta{D}(\alpha)$ ：

$$\nabla_{\alpha} \theta_D(\alpha) = 0 \ ,\ \alpha^* = -\frac{g^Tg_{ref}}{g^T_{ref}g_{ref}}$$

通过将$\alpha^*$放入上式中，A-GEM更新规则：

$$z^{*} = g- \frac{g^Tg_{ref}}{g^T_{ref} g_{ref}} = \hat g$$

Joint embedding model using compositional task descriptors

在这一部分中，将讨论如何改进包括A-GEM在内的所有LLL方法的前向迁移。

为了加速新任务的学习，我们考虑使用组合任务描述符，其中组件在任务之间共享，从而允许迁移。

例如，组合任务描述符的示例是所考虑任务的自然语言描述或指定要在任务中识别的对象的属性值的矩阵。

如果模型已经学习并记住了两个独立的属性(例如，羽毛的颜色和喙的形状)，则它可以在提供指定其属性(黄色羽毛和红色喙)的值的描述符的情况下快速识别新的类，尽管这是完全不可见的组合。

借鉴小样本学习文献中的思想，我们学习了图像特征和属性嵌入之间的联合嵌入空间。

形式上，让 $x^k \in X$ 是输入（例如，图像），$t^k$ 是大小为 $Ck × A$ 的矩阵形式的任务描述符，其中 $C_k$ 是第 k 个任务中的类数，A 是 数据集中每个类的属性总数。 联合嵌入模型由特征提取模块 $\phi{\theta}: x^k \to \phi{\theta}(x^k)$，其中 $\phi{\theta}(x^k)\in R^D$ 和任务嵌入模块 $\psi_w :t^k \to \psi_w(t^k)$，其中 $\psi_w(t^k)\in R^{C_k\times D}$ 组成 。

在这项工作中，$\phi_{\theta}(.)$ 被实现为标准的多层前馈网络，而 $\psi_w(.)$ 被实现为维度 A × D 的参数矩阵。这个矩阵可以解释为一个属性查找表，因为每个属性都与一个 D 维向量相关联，通过类中存在的属性的线性组合，从中构建类嵌入向量；

任务描述符嵌入然后是任务中存在的类的嵌入向量的串联。 在训练期间，通过最小化交叉熵损失来学习参数 θ 和 ω：

$$l_k(\theta, w) = \frac{1}{N} \sum_{i=1}^N - log(p(y_i^k| x_i^k,t^k;\theta,w))$$

其中 $(x_i^k, t^k, y_i^k)$ 是第刻个任务的第i个样本， 如果 $y_i^k=c$ 概率分布为：

$$p(c|x_i^k ,t^k;\theta, w) = \frac{exp([\phi_{\theta}(x_i^k) \psi_w(t^k)^T]_c) }{\sum_j exp([\phi_{\theta}(x_i^k) \psi_w(t^k)^T]_j)}$$

其中 $[a]_i$ 表示向量 a 的第 i 个元素。 请注意，架构和损失函数是通用的，不仅适用于 A-GEM，还适用于任何其他 LLL 模型（例如，基于正则化的方法）。