Learning to learn without forgetting by maximizing transfer and minimizing interference
Learning to learn without forgetting by maximizing transfer and minimizing interference
在对非平稳数据分布进行持续学习方面,仍然是将神经网络扩展到人类现实环境的主要挑战。
在这项工作中,我们提出了一种关于连续学习的新概念,即迁移和干扰之间的对称权衡,可以通过实施跨样本的梯度对齐来优化该权重。
Meta-Experience Replay (MER) 通过将经验回放与基于优化的元学习相结合。
该方法学习使基于未来梯度的干扰可能性较小,而基于未来梯度的迁移可能性更大的参数。
作者在连续终身监督学习基准和非静态强化学习环境中进行了实验,实验表明,MER算法和基线算法之间的性能差距随着环境变得更加不平稳和存储的经验在总经验中所占的比例变小而增大。
Continual learning problem
人工智能的一个长期目标是建立能够长期自主操作的代理。这样的代理必须渐进地学习并适应不断变化的环境,同时保持对以前所学知识的记忆,这种设置称为终身学习。本文是持续学习的一个变体。
在持续学习中,假设学习者接触到一系列任务,其中每个任务都是来自相同分布的一系列经验。
作者希望在这种情况下开发一种解决方案,在无监督的情况下发现任务的概念,同时在每次体验后逐步学习。
这很有挑战性,因为在标准的离线单任务和多任务学习中,隐含地假设数据是独立同分布的平稳分布。不幸的是,每当情况不是这样的时候,神经网络往往都会举步维艰。
持续学习面临的最大问题是灾难性的遗忘(干扰),其中最主要的担忧是神经网络缺乏稳定性,而主要的解决方案是通过专注于保留过去的知识来限制经验之间的权重共享程度。
另一个问题是稳定性-可塑性两难问题,在这种观点下,首要关注的是:网络稳定性(保存过去的知识)和可塑性(快速学习当前经验)之间的平衡。
以前的持续学习技术侧重于平衡有限的权重共享和某种机制以确保快速学。在本文中,作者扩展了这一观点,指出——对于在无限数量的分布上的连续学习,需要及时考虑前向和后向的权重共享和稳定性-塑性权衡,如下图:
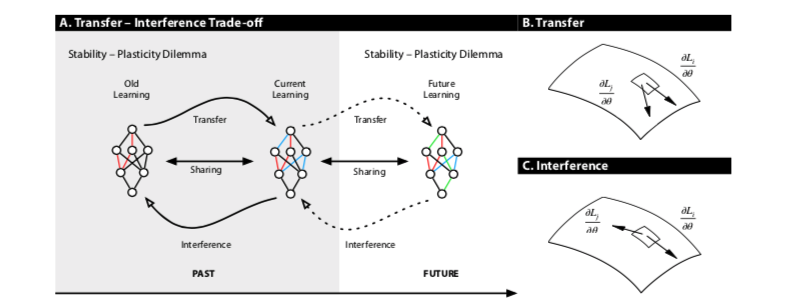
稳定性-可塑性困境考虑了当前学习的可塑性以及它如何降低旧学习。 迁移-干扰权衡考虑了稳定性-可塑性困境及其对前向和后向权重共享的依赖。这种对称的观点是至关重要的,因为单纯专注于降低权重共享程度的解决方案不太可能在未来产生迁移。
本文提出的迁移-干扰权衡为持续学习问题的梯度对齐目标提供了一个新的视角。这是问题的核心,因为这些梯度是学习期间基于 SGD 的优化器的更新步骤,并且梯度的角度和管理权重共享的程度之间存在明显的联系。
与过去对持续学习的概念观点的关键区别在于,我们不仅关注相对于过去例子的当前迁移和干扰,而且还关注随着我们学习而向前发展的迁移和干扰的动态。
然而,在过去的工作中,基于当前的学习和过去的学习,对权重共享的动态进行了临时更改,而没有制定关于最佳权重共享动态的一致理论。就我们对未来的元学习进行推广而言,这应该使模型更容易在非平稳环境中执行持续学习。
作者通过在过去关于经验回放的工作的基础上实现这一点,经验重播一直是用神经网络解决非平稳问题的中流砥柱。
作者提出了一种新的meta-experience replay(MER)算法,它结合了经验回放和基于优化的元学习。MER在各种有监督的持续学习和持续强化学习环境中显示出巨大的潜力。
The transfer-interference trade-off for continual learning
在参数 $\theta$ 和损失 $L$ 的瞬间,我们可以在使用 SGD 训练时定义两个任意不同样本 $(x_i,y_i)$ 和 $(x_j,y_j)$ 之间的迁移和干扰的操作度量。 迁移发生在:
这意味着学习样本 $ i$ 将在不重复的情况下提高示例 $j$ 的表现,反之亦然。干扰发生在:
当 $i$ 和 $j$ 使用一组重叠参数进行学习时,它们之间存在权重共享。因此,当权重共享最大化时,迁移潜力最大化,而当权重共享最小化时,干扰潜力最小化。
持续学习中稳定性-可塑性困境的过去解决方案在简化的时间环境中运行,其中学习分为两个阶段:
- 所有过去的经历都被归结为旧记忆
- 而目前正在学习的数据则是新学习
在此设置中,目标是简单地最小化时间上向后投影的干扰,这通常是通过显式或隐式地降低权重共享的程度来实现的。
然而,这种观点的重要问题是,这个系统仍然需要学习,未来会带来什么在很大程度上是未知的。这使得我们有责任不采取任何措施来潜在地破坏网络在不确定的未来有效学习的能力。这种考虑使我们将稳定性-可塑性问题的时间范围向前扩展,更一般地说,将其转变为一个持续学习问题,我们将其标记为解决迁移-干扰权衡问题。如上图A。
具体来说,重要的是不仅要减少来自我们当前时间点的反向干扰,而且我们必须以不限制我们未来学习能力的方式这样做。这种更普遍的观点承认问题中的一个微妙之处:梯度对齐的问题以及因此跨样本的权重共享在时间上向后和向前出现。
在这里,作者提出了一个潜在的解决方案,我们学习以一种在每个时间点促进梯度对齐的方式进行学习。 跨样本的权重共享可以通过迁移来提高对未来的性能,但不破坏之前的性能。 因此,我们的工作对持续学习问题采用了元学习的观点。 希望学习以一种从整体分布中推广到其他样本的方式来学习每个样本。
A system for learning to learn without forgetting
在典型的离线监督学习中,我们可以在数据集 $D$ 内$x, y$ 的平稳分布上表达我们的优化目标:
如果我们想要最大限度地迁移和最小化干扰,我们可以想象在目标上增加辅助损失以使学习过程偏向那个方向是有用的。
考虑公式1和2,一个明显有益的选择将是还直接考虑相对于在随机选择的数据点评估的损失函数的梯度。
如果我们可以最大化这些不同点的梯度之间的点积,它将直接鼓励网络在梯度方向对齐的地方共享参数,并在相反方向的梯度引起干扰的地方保持参数分开。
因此,理想情况下,针对以下目标进行优化:
其中 $(x_i,y_i)$和 $(x_j,y_j)$是随机抽样的唯一数据点。我们将尝试设计一个针对这一目标进行优化的持续学习系统。然而,要在实践中实施这种学习过程,还必须解决多方面的问题。
第一个问题是,持续学习处理的是对非平稳数据流的学习。我们通过实现一个经验回放模块来解决这个问题,该模块增强了在线学习,这样我们就可以对到目前为止看到的所有样本的固定分布进行近似优化。
另一个实际问题是,这种损失的梯度取决于损失函数的二阶导数,这一点计算效率不高。通过使用具有最小计算开销的元学习算法间接地将目标近似为一阶Tayor展开来解决这一问题。
Experience replay
Learning objective: 持续的终身学习环境对神经网络的优化提出了挑战,非平稳流中的样本层出不穷。反而,我们希望我们的网络在目前为止看到的所有样本平稳分布上进行优化。经验回放 (1992) 是一种古老的技术,它仍然是尝试在非平稳环境中学习的深度学习系统的核心组成部分,我们将在这里采用最近工作中的约定 (A deeper look at experience replay2017) ; Scalable recollections for continual lifelong learning2017) 利用这种方法。
经验回放的中心特征是保持对所见样本的记忆 $M$,该记忆与当前样本的训练交织在一起,目的是使训练更稳定。因此,经验回放在 $M$ 逼近 $D$ 的程度上逼近等式 3 中的目标:
$M$ 具有当前大小 $M{size}$和最大大小$M{max}$。 使用reservoir sampling来更新缓冲区。这确保在每个时间步,看到的 N 个示例中的任何一个在缓冲区中的概率都等于 $M_{size}/N$。
缓冲区的内容类似于所有样本的平稳分布,以至于存储的项目捕获了过去样本的变化。 遵循离线学习的标准做法,我们通过从 M 捕获的分布中随机抽样一批 B 来进行训练。
Prioritizing the current example: 我们探索的经验回放变体与离线学习的不同之处在于,当前样本具有特殊作用,可确保它始终与从回放缓冲区采样的样本交错。这是因为在我们继续下一个样本之前,我们希望确保我们的算法能够针对当前样本进行优化(特别是如果它没有添加到记忆中)。在看到的N个样本上,这仍然意味着我们已经将每个样本作为当前样本进行了训练,每步的概率为1/N。我们提供了进一步详细说明在这项工作中如何使用经验回放的算法在附录G中。



Concerns about storing examples: 显然,将所有经验都存储在内存中是不可行的。因此,在这项工作中,我们重点展示当每种方法只提供很小的内存缓冲区时,我们可以获得比基线技术更高的性能。
Combining experience replay with optimization based meta-learning
First order meta-learning:
FOMAML 和 Reptile
Reptile通过泰勒展开指出,这两个算法对于相同的损失函数是近似优化的。Reptile可以有效地针对大致相同的目标进行优化,同时不需要像 MAML 那样针对每个学习的任务将数据拆分为训练和测试拆分。Reptile 是通过使用基于 SGD 的优化器和学习率 $\alpha$ 顺序优化 s batch数据来实现的。在对这些批进行训练之后,我们在训练 $\theta_0$ 之前获取初始参数,并将它们更新为 $\theta_0 \leftarrow \theta_0 + \beta *(\theta_k-\theta_0)$,其中 $\beta$ 是元学习更新的学习率。
该过程对每个系列的s批进行重复(算法2)。Reptile在一组s批次中大致优化了以下目标:

The MER learning objective: 在这项工作中,我们修改了Reptile算法,将其与经验回放模块适当地集成在一起,在最大化迁移和最小化干扰的同时,促进了持续学习。
正如我们在附录I中的推导过程中更详细地描述的那样,在按顺序提供样本的在线设置中实现 Reptile 目标并非易事,并且只能部分实现,因为我们对缓冲区和批次的采样策略。根据上一节关于体验回放的评论,这允许我们使用MER算法在持续学习环境中针对以下目标进行优化:
The MER algorithm: MER 使用储层采样维护经验回放式记忆 M,并在每个时间步从缓冲区中抽取 s 个批次,包括 k-1 个随机样本,以与当前示例一起训练。每个批次内的k个样本中的每一个都被视为其自己的大小为1的Reptile批次,在该批次被处理之后具有内循环爬行动物元更新。然后,我们在外部循环中跨s个批次再次应用Reptile元更新。我们在算法1中提供了关于MER的更多细节。当β=1时,该过程近似于上面的目标。采样函数生成 s 个更新批次。 通过首先添加当前示例然后从 M 中交错 k - 1 个随机样本来创建每个批次。

Prioritizing current learning: 为了确保强正则化,我们希望在 Reptile 更新中处理的批次数量足够大 - 足以让经验重播开始过拟合 M。因此,我们还需要确保我们提供足够的优先级来学习当前样本,特别是因为我们可能不会将其存储在 M 中。为了在算法 1 中实现这一点,我们从 M 中采样 s 个单独的批次,这些批次按顺序处理并且每个批次都与当样本交错。
实验
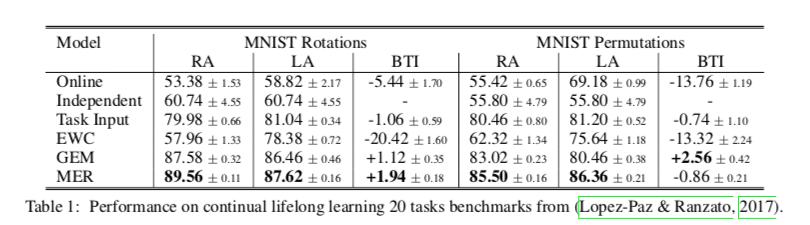
How does MER perform on supervised continual learning benchmarks?
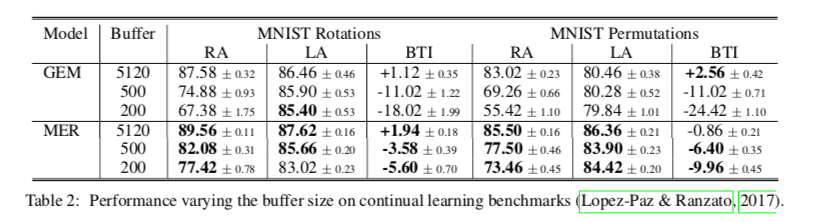
How do the performance gains from MER vary as a function of the buffer size?
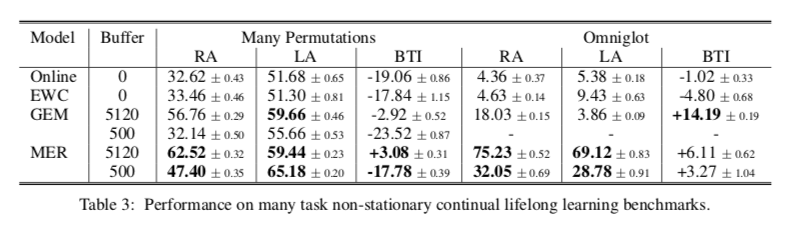
How effective is MER at dealing with increasingly non-stationary settings?
Does MER lead to a shift in the distribution of gradient dot products?








