La-MAML: Look-ahead Meta Learning for Continual Learning
La-MAML: Look-ahead Meta Learning for Continual Learning
持续学习问题涉及能力有限的训练模型,这些模型在一组未知数量的顺序到达的任务上表现良好。
虽然元学习在减少新旧任务之间的干扰方面显展示出潜力,但目前的训练过程往往要么很慢,要么离线,而且对许多超参数很敏感。
作者提出Look-ahead MAML (La-MAML) 一种optimisation-based的快速元学习算法,用于在线持续学习,并辅之以小情节记忆。
作者在元学习更新中提出的对每个参数学习率的调制,并将其与先前关于超梯度 hypergradients 和元下降 meta-descent 的工作联系起来。
与传统的基于先验的方法相比,这提供了一种更灵活和更有效的方式来减轻灾难性遗忘。
作者开发了一种基于梯度的元学习算法,以实现高效的在线持续学习。先提出了一种连续元学习的基本算法,称为连续MAML(C-MAML),它利用replay-buffer并优化了一个减轻遗忘的元目标。随后提出了一种对C-MAML的改进,称为La-MAML,它包括对每参数学习率(LRs)的调制,以跨任务和时间调整模型的学习速度。
连续学习与元学习
涉及论文
- GEM:Gradient episodic memory for continual learning.
- MER:Learning to learn without forgetting by maximizing transfer and minimizing interference (2019)
- Reptile:On first-order meta-learning algorithms (2017)
- 12:Meta-learning representations for continual learning. (2019)
- Generative-replay:Continual learning with deep generative replay. (2019)
- A-GEM:Efficient lifelong learning with a-GEM (2019)
- Online-aware Meta Learning (OML) : Meta-learning representations for continual learning (2019)
- 2 : Continuous adaptation via meta-learning in nonstationary and competitive environments (2018)
- 10 : Online meta-learning (2019)
- 19:Continual adaptation for model-based RL (2019)
- BGD:Task Agnostic Continual Learning Using Online Variational Bayes
- UCB:Uncertainty-guided continual learning with bayesian neural networks
- AlphaMAML : Adaptive Model-Agnostic Meta-Learning.
灾难性的遗忘是Continual Learning的最大的挑战之一,当随机梯度下降(SGD)所需的i.i.d.采样条件被违反时,可能会发生这种情况,因为属于要学习的不同任务的数据按顺序到达。
连续学习(CL)算法还必须有效地利用其有限的模型容量,因为未来任务的数量是未知的。因此,确保各任务之间的梯度对齐至关重要,以便在实现其目标方面取得共同进展。
梯度情节记忆(GEM)研究了CL中权重分担和遗忘之间的关系,并开发了一种显式尝试最小化梯度干扰的算法。
Meta Experience Replay(MER)形式化了迁移-干扰权衡,并表明GEM的梯度排列目标与一阶元学习算法Reptile优化的目标一致。
除了对齐梯度外,元学习算法对 CL 也很有前景,因为它们可以直接使用元目标来影响模型优化并改进泛化或迁移等辅助目标。这避免了为了更好的CL而定义诸如稀疏性这样的启发式激励。缺点是它们通常很慢,很难调整,使它们更适合离线继续学习[12]。
持续学习
方法大致三种类型 replay-based, regularisation (or prior-based) 和 meta-learning-based .
- replay-based:为了避免灾难性遗忘的问题,replay-based的方法在内存中维护以前任务的样本集合。利用情节缓冲器(episodic-buffer)统一采样旧数据以模拟独立同分布的方法。Generative-replay训练生成模型能够重放过去的样本,但由于复杂的非平稳分布建模的困难而引起的可扩展性问题。GEM和A-GEM将存储器样本考虑在内,来确定改变的低干扰梯度以更新参数。
- Regularisation-based:是一种启发式的方法,确保保留先前任务的性能的来约束网络权重,从而完全避免使用重放。这包括惩罚被认为对旧任务很重要的权重的改变,或者强制实施权重或表征稀疏性,以确保在任何时间点只有一部分神经元保持活跃。
- Meta-Learning-based:这些方法是最近才出现的。MER 受 GEM 的启发,利用重放来激励新旧任务之间的梯度对齐。 OML引入了用于预训练算法的元目标,以离线学习最优表示,该最优表示随后被冻结并用于CL。[2,10,19]研究正交设置,其中学习代理使用所有先前看到的数据来快速适应传入的数据流,从而忽略灾难性遗忘的问题。
预备知识
首先通过顺序地观察 $T$ 个任务的训练数据$[D_1,D_2,…,D_T]$ 来学习 $T$ 个任务的序列 $[\tau_1,\tau_2 ,…,\tau_T]$
定义$X^i,Y^i = {(xn^i,y_n^i)}{n=0}^{N_i}$ 为$N_i$个输入标签集合从数据 $D_i$ 中随机抽取。
在在线学习过程中的任意时间步长 $j$,我们的目标是最小化模型在迄今看到的所有 $t$ 个任务上的经验风险 $(τ_{1:t})$,给定对来自先前任务 $τ_i(i<t)$ 的数据 $(X_i,Y_i)$ 限制访问。我们将这一目标称为累积风险,具体如下:
其中 $l_i$ 是在任务$\tau_i$上的loss, $f_i$ 是学习器,参数 $θ_0^j$ 是从输入到输出的特定任务映射参数。
$Lt = \sum{i=1}^t li$ 是任务 $τ{1:t}$ 的所有任务损失之和,其中 $t$ 从 1到 $T$ 。设 $l$ 表示要最小化的某些损失目标。
作用于参数$θ_0^j$ (由 $U(θ_0^j)$ ) 表示的SGD运算定义为:
$U$ 可以为 $U_k(\theta_0^j) = U…\circ U\circ U(\theta_0^j) =\theta_k^j$
Model-Agnostic Meta-Learning (MAML):
meta learning 成为一种流行的训练模型的方法,能够在有限的数据上进行快速调整。MAML建议优化模型参数,以学习一组任务,同时改进辅助目标,如任务分布中的few-shot 少样本泛化。
基于梯度的元学习中使用的一些常用术语:
初始化:在训练期间的给定时间步长 $j$ 处,模型参数 $θ_0^j$ (或为简单起见,$θ_0$)通常被称为初始化,因为其目的是找到对不可见数据进行 few-shot 基于梯度的适配的理想起点。
inner-updates 快速或内部更新:是对 $θ_0$ 的副本进行基于梯度的更新,以优化某些内部目标(在本例中,对于某些$τ_i$,为$l_i$)。
meta-update:元更新涉及从 $θ0$ 到 $θ_k$ 的快速更新的轨迹,然后进行到 $θ_0$的永久梯度更新(或缓慢更新)。该缓慢更新是通过评估 $θ_k$ 上的辅助目标(或元损失meta loss $L{meta}$)并通过轨迹微分以获得$\nabla{\theta_k}L{meta}(\thetak)$来计算的。因此,MAML在时间步 $j$ 优化 $θ_0^j$,以便在对它们的样本进行几次梯度更新之后,对 ${\tau{1:t}}$中的任务执行最佳性能。它在每一次元更新中都进行了优化,目标是:
元学习与持续学习目标的等价性:
Reptile证明了Reptile算法和MAML算法等一阶和二阶元学习算法的近似等价性
MER随后表明,他们的CL目标是在一组任务$\tau_{1:t}$之间最小化损失并调整梯度,直到任何时间 $j$(在左边),可以通过Reptile目标(在右边)进行优化,即:
其中 meta-loss $Lt = \sum{i=1}^t li$ 根据Tasks $\tau{1:t}$中的样本进行评估。这意味着元学习初始化的过程与学习CL的最优参数一致。
在线感知元学习(OML):
[12]提出了元学习 Representation-Learning Network 网络(RLN)的概念,为Task-Learning Network (TLN)提供适合协作学习的表示。
RLN的表示是在离线阶段学习的,在该阶段使用灾难性遗忘作为学习信号进行训练。当TLN经历时间相关更新时,来自固定任务集($\tau_{val}$)的数据被反复用于评估RLN和TLN。
在每个元更新的内循环中,TLN使用冻结的RLN对流式任务数据进行快速更新。然后,通过根据来自$\tau_{val}$的数据以及当前任务计算的 meta loss来评估RLN和更新的TLN。
这将测试在尝试学习流任务的过程中,模型在 $\tau_{val}$ 上的性能发生了怎样的变化。然后对meta loss进行微分,以获得针对TLN和RLN的缓慢更新的梯度。
这两个loss的组合被称为OML目标,以模拟内环中的CL和测试外环中的遗忘。RLN学习最终为CL的TLN提供更好的表示,该表示被证明具有紧急稀疏性。
Method
在上一节中,我们看到OML目标可以直接规范CL行为,并且MER利用了元学习和CL目标的近似等价性。我们注意到,OML离线训练静态表示和MER算法慢得令人望而却步。
作者表明,通过多步MAML过程在线优化OML目标等同于更有效的样本效率CL目标。
Continual-MAML (C-MAML)
C-MAML旨在在线优化OML目标,这样学习当前任务就不会导致忘记以前见过的任务。我们定义了这个目标,适用于优化模型的参数 θ 而不是时间步 j 的表示,如下所示:
其中 $Sk^j$ 是来自前任务$\tau{t}$ 中的k个数据元组的流 $(X{j+l}^t,Y{j+l}^t)^k$ ,这是模型在时间 $j$ 处看到的。
Meta loss $Lt = \sum{i=1}^l li$ 在 $\theta{k}^j = Uk(\theta{0}^j ,S_k^j)$ 上评估。它评估 $\theta_k^j$ 对于上面第一个公式中定义的持续学习预测任务的适合性,直到$\tau_t$.
省略了隐含的数据参数 $(x^i,y^i) \sim (X^i,Y^i)$ 这是任何任务$\tau_i$的 $L_t$ 中每个损失 $l_i$ 的输入。附录B
与上文元学习与合作学习目标的等价性那个公式不同它是不对称的,它集中于对其$\taut$的梯度和$\tau{1:t}$的平均梯度,而不是在任务$\tau_{1:t}$之间对齐所有成对梯度。附录D
作者的经验表明,旧任务之间的梯度对齐不会退化,而学习了新任务,避免了重复优化它们之间的任务间对齐的需要。
这导致MER目标的显著加速,该目标试图将所有$\tau_{1:t}$ 上相乘均匀分布的批次。由于每个s 在梯度更新中有 $1/t-th$ 次贡献,因此MER有必要对包括s在内的许多此类均匀批次进行多次传递。
在训练期间,如MER中所示,通过对输入数据流的存储采样来填充重放缓冲器R。
在每次元更新开始时,从当前任务中采batch b。b还与从R采样的批次组合以形成元批次meta-batch $bm$,其表示来自旧任务和新任务的样本。$\theta_0^j$通过k个基于sgd的内部更新进行更新,每次从b查看一个当前任务的样本。外部损失或元损失$L_t(\theta_k^j)$是在$b_m$上评估的。它指示参数 $\theta_k^j$ 在时间 $j$ 之前看到的所有任务 $\tau{1:t}$上的性能。 附录C
Lookahead-MAML (La-MAML)
尽管元学习激励了任务内和任务间组的梯度对齐,但在新旧任务的梯度之间仍然可能有一些干扰,$\tau{1:t−1}$和 $\tau{t}$。
这将导致忘记 $\tau{1:t−1}$,因为它的数据不再对我们完全可用。在训练新任务的开始阶段尤其如此,因为新任务的梯度不一定与旧任务一致。因此,需要一种机制来确保元更新相对于$\tau{1:t-1}$是保守的、避免负迁移。元更新的幅度和方向需要根据更新对 $\tau_{1:t-1}$ 损失的影响程度进行调整。La-MAML包括一组可学习的pre-parameter学习率(LR),用于内部更新,如图1所示。
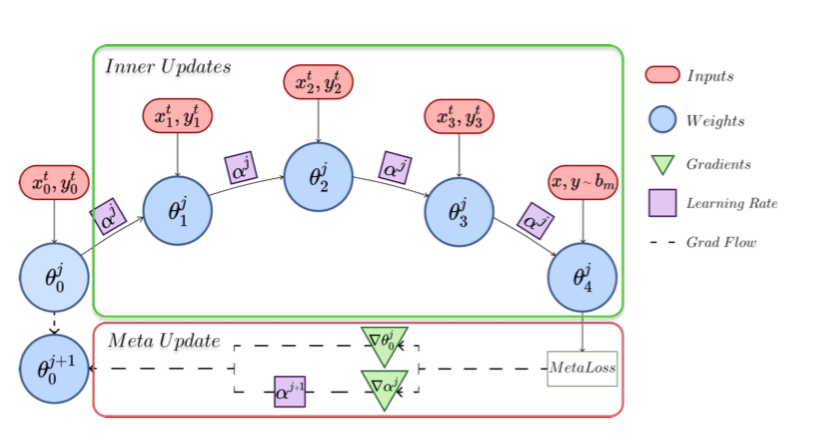
对于每批数据,初始权重经历一系列 $k$ 次快速更新以获得 $\theta_k^j$ (这里 $j=0$),其针对元损失进行评估以相对于权重 $\theta_0$ 和LRs $\alpha_0$ 反向传播梯度。首先,$\alpha^0$更新为$\alpha^1$,然后用于将 $\theta_0^0$更新为 $\theta_0^1$,蓝色框表示快速权重,绿色框表示慢速更新的梯度。LRs和权重以异步方式更新。
这是因为我们观察到上面OML的方程的梯度相对于内循环的 LR 的表达式直接反映了旧任务和新任务之间的对齐情况。扩充的学习目标被定义为:
以及该目标在时间 $j$ 的梯度,相对于 LR 向量 $\alpha^j$ (定义为$g_{MAML}(\alpha^j)$):
附录A推导
$g{MAML}(\alpha)$ 中的第一项对应于元损失的梯度在batch上 $b_m:g{meta}$。第二项表示来自内部更新的累积梯度:$g_{traj}$。
该表达式表明,当$g{meta}$和 $g{traj}$之间的内积较高时,LRs的梯度将为负,即两者对齐;当两者正交(不干扰)时为零,当两者之间存在干扰时为正。
负的(正的)LR梯度会拉高(降低)LR的大小。如下图:
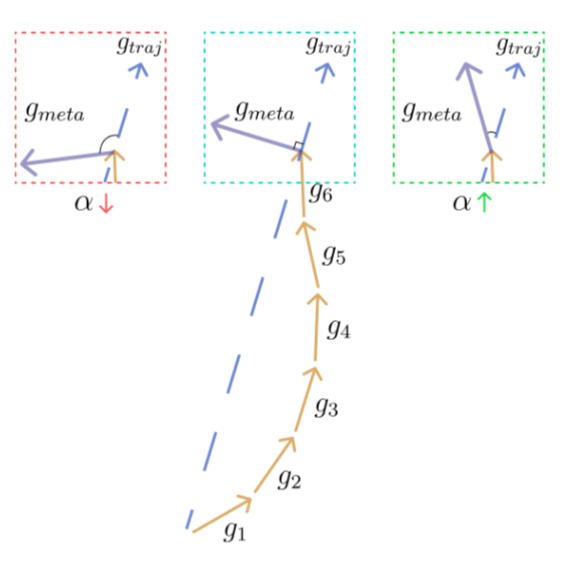
$g{traj}$ (蓝色虚线)和 $g{meta}$对齐的不同场景,从扰动(左)到对齐(右)。黄色箭头表示内部更新。当梯度对齐(扰动)时,LR $\alpha$
增加(减少)。
我们建议在元更新中异步更新网络权重和LRs。设$\alpha^{j+1}$ 为更新的LR 向量,该向量通过在时间 $j$ 处采用上一个等式中的LR梯度进行SGD而获得。然后,我们将权重更新为:
其中k是在内循环中采取的步数。 将 LRs $\alpha^{j+1}$ 修剪为正值,以避免上升梯度,并且也避免进行扰动的参数更新,从而减轻灾难性遗忘。因此,元目标保守地调节学习的速度和方向,以便在新任务上取得更快的学习进度,同时促进旧任务的迁移。

Line(a),(b)是C-MAML和La-MAML之间的唯一区别,C-MAML使用固定标量LR $\alpha$ 进行元更新到 $\theta_0^j$,而不是 $\alpha^{j+1}$。
作者的基于元学习的算法结合了基于先验和基于回放的方法的概念。LR在重放样本上的梯度和流任务之间的相互作用的指导下,以数据驱动的方式调制参数更新。然而,由于LR随着每次元更新而演变,它们的衰变是暂时的。这与许多基于先验的方法不同,在这些方法中,对参数更改的惩罚逐渐变得非常高,以至于网络容量饱和。
随着任务的到来,可学习的LR可以调整为高值和低值,因此是一种更简单、灵活和优雅的约束权重的方法。这种异步更新类似于信任区域优化或前瞻搜索,因为每个参数的步长是根据对它们应用假设更新后产生的损失进行调整的。
与其他工作的联系
Stochastic Meta-Descent (SMD)
当学习非平稳数据分布时,使用衰减的LR策略并不常见。严格递减 LR 策略旨在更接近收敛于固定分布的固定 mimima,这与在线学习的目标不一致。由于数据分布的范围未知,因此也不可能手动调整这些计划。
然而,LRS的适应性仍然是非常需要的,以适应优化的场景,加速学习,调节适应的程度,以减少灾难性遗忘。我们的自适应LRS可以连接到离线监督学习(OSL)中的元下降。虽然存在几种不同的变种,但它们背后的核心思想和我们的方法是获得适应。当我们根据新旧任务梯度之间的相关性调整增益以在所有任务上共享进展时,[4,25]利用两个连续随机梯度之间的相关性来更快地收敛。我们利用元目标关于LRS的可微性,自动获得LR超梯度。
Learning LRs in meta-learning
Meta-SGD 建议学习MAML中的LRS以进行few-shot学习。他们的更新和我们的更新有一些显著的不同。它们同步更新权重和LR,而我们对LRS的异步更新用于执行更保守的权重更新。
我们更新的直觉来自于需要减轻梯度干扰及其与持续学习中普遍存在的转移-干扰权衡的联系。α-MAML解析地更新了MAML更新中的两个标量LR,以实现更自适应的few-shot学习。我们的每个参数的LR通过反向传播被隐式地调制,以基于它们在任务之间的排列来调节参数的变化,为我们的模型在CL领域提供了更强大的适应性。
实验
指标
使用保留精度retained accuracy(RA)度量来比较各种方法。RA 是模型在训练结束时跨任务的平均准确率。
反向迁移和干扰 backward-transfer and interference(BTI)值,它衡量每个任务从学习到最后一个任务结束的准确性的平均变化。 较小的 BTI 意味着训练期间遗忘较少。
Efficient Lifelong Learning (ELL): 高效终身学习 (LLL):在A-GAM中形式化,高效终身学习的设置假设每个任务的传入数据必须仅通过一次处理:一旦处理,数据样本将不再可访问,除非它们被添加到 回放记忆。
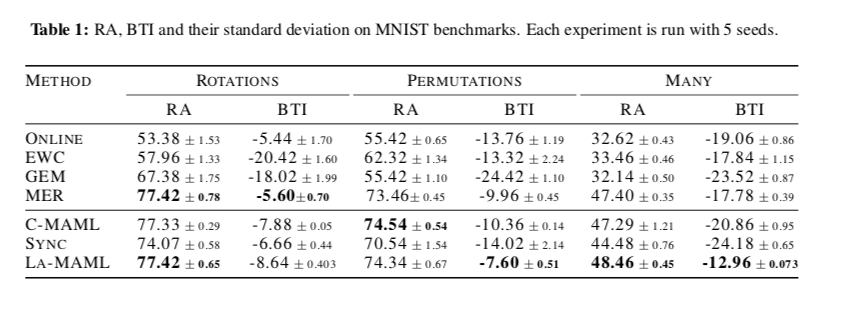
随着训练的进行,模型会演变成对遗忘的抵抗力。这意味着超过一个点,它可以在传入样本的一个小窗口上持续进行梯度更新,而不需要进行元更新。