Rethinking Graph Transformers with Spectral Attention
Rethinking Graph Transformers with Spectral Attention
提出了Spectral Attention Network(SAN),它使用学习的位置编码(LPE),可以利用全拉普拉斯频谱来学习给定图中每个节点的位置。通过利用拉普拉斯的全谱,模型在理论上具有强大的区分图形的能力,并且可以更好地从它们的共振中检测出相似的子结构。
在这项工作中,作者还是研究如何将Transformer体系结构应用于图形表示学习。开发了强大的可学习的位置编码方法,这些方法植根于谱图理论。 谱注意力网络(SAN)架构解决了先前图形转换器工作中的关键理论限制,并且明显超过了标准消息传递GNN的表达能力。
SAN方法的优势对比:
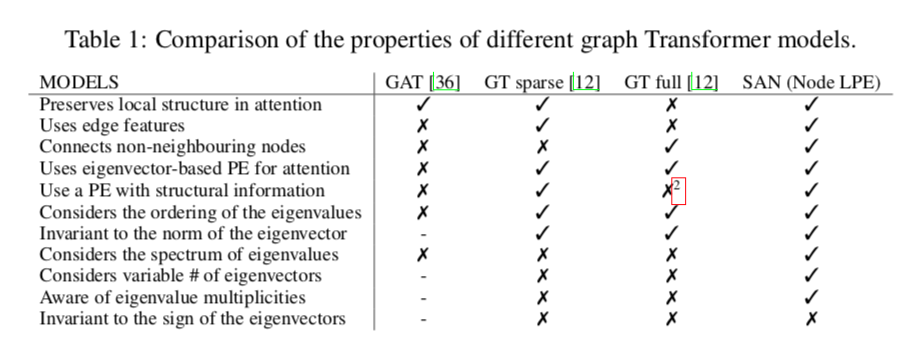
- 保持注意中的局部结构
- 使用边特征
- 连接非相邻节点
- 使用基于特征向量的PE进行注意
- 使用具有结构信息的PE
- 考虑特征值的排序
- 特征向量的范数不变量
- 考虑特征值的谱 (SAN独有)
- 考虑特征向量的变量# (SAN独有)
- 意识到特征值的多重性 (SAN独有)
- 对特征向量的符号不变
也就是说SAN结合了稀疏和稠密GT的特性,并且还考虑了特征值的谱、征向量的变量#、意识到特征值的多重性。
基于特征函数的绝对和相对位置编码
因为不存在对节点进行排序或定义轴的规范方法。在本节中,作者将研究如何使用拉普拉斯的特征函数来定义图形中的绝对和相对PE,测量节点之间的物理相互作用,并使特定的子结构能够“听到”-类似于鼓的声音,揭示其结构。
特征向量等价于图上的正弦函数
在Transformer架构中,一个基本方面是使用正弦和余弦函数作为序列的PE。然而,对于任意图形,sinusoids正弦不能被清楚地定义,因为沿轴的位置没有清晰的概念。取而代之的是,它们的等价性由图Laplacian L的特征向量 $\Phi$ 给出。
事实上,在欧几里得空间中,拉普拉斯算子对应于梯度的散度,其特征函数是正弦/余弦函数,平方频率对应于特征值(我们有时从这里起将这两个概念互换)。因此,在图域中,图的Laplacian的特征向量与正弦函数自然等价,并且这一直觉被用于最近的多项工作中,这些工作将特征向量用作GNN(Benchmarking graph neural networks)、定向流(Directional graph networks. ICML2021)和GT的PE。
在与正弦函数等价的情况下,我们很自然地发现,$\mathcal{F}[f]$的傅里叶变换函数应用于图$\mathcal{F}f = \langle f, \phi_i \rangle$,其中特征值被认为是该图的傅立叶域中的一个位置。因此,最好将特征向量视为位于特征值轴上的向量,而不是矩阵的组成部分,如图所示。

关于相对位置,特征函数告诉我们什么?(物理应用)
除了模拟正弦函数外,拉普拉斯函数的特征向量还包含有关系统物理的重要信息,可以揭示距离度量。因为拉普拉斯运算符是物理学中的一个基本运算符,在麦克斯韦方程和热扩散中都有显著的应用。
在电磁理论中,拉普拉斯的(伪)逆,在数学上称为拉普拉斯的格林函数,表示电荷的静电势。
在图中,相同的概念使用拉普拉斯G的伪逆,并且可以通过其特征函数来计算。
如下公式,$G(j_1,j_2)$ 是节点$j_1,j_2$ 之间的电势。 $\hat \phi_i,\hat \lambda_i$ 为对称Laplacian$D^{\frac{-1}{2}}LD^{\frac{-1}{2}}$第 $i$个特征值和特征向量。
此外,傅立叶给出的热方程的原始解依赖于被称为傅立叶级数的正弦/余弦的和。由于拉普拉斯函数的特征向量是这些函数在图中的近似,我们找到了近似的解。热核与随机游走相关,我们利用两个热核之间的相互作用在下面方程中定义节点$j_1,j_2$之间的扩散距离$d_D$。类似的二次谐波距离$d_B$是一种不同的距离测量方法。这里我们使用正则拉普拉斯L的特征函数:
这个方程,首先强调了在提供有关图中相对位置的信息时将特征向量与其对应的特征值配对的重要性。其次,我们注意到特征向量的乘积与静电相互作用成正比,而减法与扩散距离和重谐距离成正比。最后,所有3个方程都有一个一致的模式:在确定节点之间的距离时,频率/特征值越小,权重越大。
听图的形状及其子结构
特征值的另一个众所周知的性质是它们如何用于区分不同的图结构和子结构,因为它们可以解释为图的共振频率。
这就引出了一个著名的问题,即我们是否能从鼓的特征值中听到鼓的形状,同样的问题也适用于几何物体和3D分子。
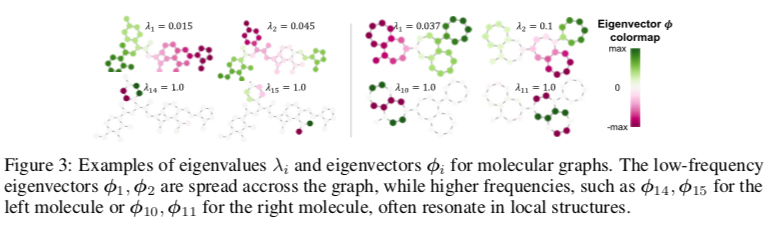
通过将特征函数用于部分功能对应、算法理解几何和样式对应。分子图的特征向量的例子如图所示。
Laplace Eigenfunctions的规范
在欧几里德空间和序列中,使用正弦波作为PE是很简单的:我们可以简单地选择一组频率,计算正弦波,并将它们添加或拼接到输入嵌入,就像在原始变压器中所做的那样。然而,在任意图中,复制这些步骤并不那么简单,因为每个图都有一组唯一的特征函数。
在接下来的部分中,将介绍谱图理论中的关键原则,在为图构造PE时要考虑这些原则,这些原则大部分被以前的方法忽略了。包括正则化,特征值及其多样性的重要性,特征向量的数量是可变的,以及符号模糊性。作者的LPE架构旨在解决这些问题。
Normalization 给定拉普拉斯的特征值,就有一个维数大于1的相关特征空间。为了在模型中利用这些信息,必须选择一个单一的特征向量。在我们的工作中,我们使用L2正则化,因为它与格林公式也就是上面的第一个公式的定义是兼容的。因此,我们将始终选择特征向量$\phi$,使$⟨\phi,\phi⟩=1$。
Eigenvalues 另一个基本方面是与每个特征向量相关联的特征值提供了有价值的信息。基于特征向量的特征值的排序在序列中起作用,因为频率是预先确定的。然而,这一假设在图中不起作用,因为它们的谱中的特征值可以改变。例如,在上图中,我们观察到排序如何忽略两个分子在 $λ = 1$ 以不同方式共振的事实。
Multiplicities 选择特征函数的另一个重要问题是特征值高度多样的可能性,即当一个特征值多次作为特征多项式的根出现时。在这种情况下,相关联的特征空间可以具有2维或更多维,因为我们可以从具有相同特征值的任何特征向量的线性组合中生成有效的特征向量。这进一步复杂化了选择用于算法计算的特征向量的问题,并突出了拥有能够处理这种歧义的模型的重要性。
Variable number of eigenvectors 图 $G_i$ 至多可以有 $N_i$ 个线性独立的特征向量,其中 $N_i$ 是它的节点数。最重要的是,$N_i$ 可以在数据集中的所有的 $G_i$ 都有所不同。GT选择了固定数目的k个特征向量给每个图,其中 $k≤N_i$,$∀i$。当数据集中最小的图的节点比最大的图少得多时,这就产生了一个主要的瓶颈,因为很小比例的特征向量将用于大型图。这不可避免地造成信息丢失,并激发了对构建k维固定PE的模型的需求,其中k不依赖于图中的特征向量的数目。
Sign invariance 如前所述,特征向量存在符号歧义。由于φ的符号与它的正则化无关,在选择图的k个特征向量时,我们只剩下2k个可能的符号组合。以前的工作已经提出通过随机反转特征向量的符号来进行数据增强,虽然当k较小时可以工作,但是对于较大的k会变得困难。
Model Architecture
我们提出了一种体系结构,它可以使用特征函数作为PE,同时解决上述规范中提出的问题。我们的 Spectral Attention Network (SAN)模型输入图的特征函数,并将其投影到固定大小的学习位置编码(LPE)中。LPE允许网络使用每个图的整个拉普拉斯频谱,学习频率如何交互,并决定哪些频率对给定任务最重要。
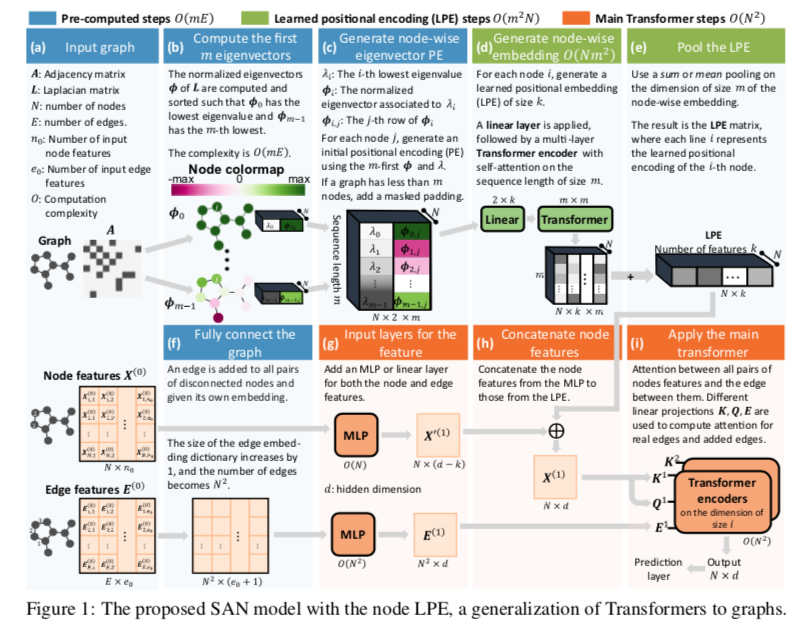
如图分为两步学习过程。
图中的(c-d-e)描述了第一步,在每个节点的特征函数上应用一个Transformer,为每个图生成一个LPE矩阵。
然后将LPE连接到节点嵌入图中(g-h),然后将其传递给Graph Trabsformer (i)。如果任务涉及图分类或回归,则最终节点嵌入随后将传递到最终池化层。
LPE Transformer Over Nodes
使用拉普拉斯编码作为节点特征在有关该主题的文献中是普遍存在的。LPE的想法受到上面第二个图的启发,其中特征向量 $\phi$ 被表示为一个非均匀序列,特征值λ是频率轴上的位置。使用此表示法,Transformers是处理它们并生成固定大小PE的自然选择。
LPE结构如图所示:

学习位置编码(LPE)结构,模型通过考虑m个特征值和特征向量来学习图的拉普拉斯谱,其中允许 $m≤N$,其中N表示节点数。
首先,我们通过将m个最低特征值与其关联的特征向量连接起来,为每个节点$j$ 创建一个大小为 $2×m$ 的嵌入矩阵。这里,m是要计算的特征向量的最大数目的超参数,并且类似于标准变压器的可变长度序列。对于 $m>N$ 的图,只需添加掩码填充。注意,要捕获所有图的整个谱,只需选择m,使其等于图在数据集中具有的最大节点数。然后在大小为2的维度上应用线性层以生成大小为k的新嵌入。然后,Transformer编码器对长度为m且隐藏维数为k的序列计算self-attention。最后,sum pooling将该序列简化为固定的k维节点嵌入。
通过将特征值与归一化特征向量连接起来,该模型直接处理前三个规范。即将特征向量归一化,将特征向量与其特征值配对,并将特征向量的个数作为变量。此外,该模型意识到了多重性,并且有可能线性组合或忽略一些重复的特征值。
然而,这种方法仍然没有解决预先计算的特征向量的符号是任意的限制。为了解决这个问题,我们像以前的工作[13,12]所采用的那样,在训练过程中随机反转预先计算的特征向量的符号,以促进符号歧义的不变性。







