GPT-GNN: Generative Pre-Training of Graph Neural Networks
GPT-GNN: Generative Pre-Training of Graph Neural Networks
Self-Supervised Learning分成两种方法:一种是生成式模型,一种是判别式模型(对比学习)。
以输入图片信号为例,生成式模型,输入一张图片,通过Encoder编码和Decoder解码还原输入图片信息,监督信号是输入输出尽可能相似。判别式模型,输入两张图片,通过Encoder编码,监督信号是判断两张图是否相似(例如,输入同一个人的两张照片,判断输入相似,输出1;输入两个人的照片,判断输入不相似,输出0)。
文章贡献
继上一文 Strategies for Pre-training Graph Neural Networks 对预训练GNN做了大规模的实验,并提出提出了一种结合节点级和图级表示的预训练方法,优化了单单使用一种级别做预训练后产生的负迁移效果。
又以生成式自监督的方式,来在预训练阶段捕捉图数据的结构信息和语义信息。分别是边生成任务和属性生成任务。
它们联合优化等价于最大化整个属性图的概率似然,这样预训练模型可以捕捉到节点属性与图结构之间的内在依赖关系。
预训练的GNN网络目标主要是异质单个(大规模)图上预训练,并进行节点级迁移。
然后优化了预训练模型可以让其处理大规模的图采样子图,采用的是通过自适应的嵌入队列,减轻负采样带来的不准确损失。
接下来主要介绍两种自监督任务和这个优化方法。
行文逻辑
通过行文逻辑,学习怎么写论文。
首先作者先是说GNN有用,预训练GNN刚刚被证明有用!接下来从充分利用无标签数据做无监督任务说,大规模的图数据标记成本昂贵。NLP的数据也一样标注昂贵,所以有了bert那样的预训练语言模型,并且提高了下游任务性能。同样在cv领域也是。
列举了GAE、GraphRNN、半监督GCN等图生成技术,但他们不适合用于预训练GNN。因为:首先,它们大多只关注于生成无属性的图结构,而没有定义节点属性与图结构之间的底层模式,图结构是GNNs中卷积聚合的核心。其次,它们被设计用来处理迄今为止的小图形,限制了它们在大规模图形上进行预训练的潜力。
然后介绍了下预训练和finetuning的流程,就不多说了。
然后切入正题介绍他的贡献,上文介绍过。
然后是准备工作和相关工作,介绍GNN的传统机制,信息传递和信息聚合的基本原理,不多介绍。
和GNN发展历史,其中有一个Graph Infomax 最近可能要学习一下,最大化了从GNNs获得的节点表示和图pooling表示之间的互信息,也就是节点级和图级。作者认为其,在纯监督学习环境下表现出改进,但学习任务通过强迫附近节点具有相似的嵌入来实现,而忽略了图的丰富语义和高阶结构。
介绍预训练在cv和nlp的成功。不过我最近听说cv圈有一篇文章,最近2021的有一篇预训练CNN其效果并不比基于transformer的模型差。
介绍生成预训练任务的数学定义,之后是具体细节和模型方法,再到实验结论等等。
关于生成式预训练任务的框架流程
形式上给出图数据 $G = (V,E,X)$ 和GNN模型 $f_{\theta}$
我们通过这个GNN将此图上的可能性建模为 $p(G;θ)$ ——-表示G中的节点是如何属性化和连接其他节点的(可以理解为先验知识)。
其目的是通过最大化图的似然,得到参数 $θ^∗=max_{θ}p(G;θ)$ 来预先训练广义神经网络模型。
那么问题变成了如何对 $p(G;\theta)$ 进行适当的建模。
现在大多的现有图生成方法都是遵循自回归方式来分解目标概率分布,也就是图中的节点是按顺序来的,并且边是通过将每个新到达的节点连接到现有节点来生成的。什么是自回归?
如上式,c 为常数项,$\epsilon$ 为随机误差,概况来说就是X的当前期值等于一个或数个前期值的线性组合加常数项和睡觉误差。
类似的作者也通过一个排列向量 $\pi$ 来确定节点顺序,其中 $i^{\pi}$ 表示向量中第i个位置的节点id。因此,图的分布$p(G;\theta)$ 等价于所有可能排列上的期望似然:
其中$X^{\pi} \in R^{|V|\times d}$ ,$E$ 是边集 ,$E_{i}^{\pi}$ 表示所有连接节点$i^{\pi}$ 的边。
为简单起见,假设观察到任何节点排序 $π$ 的概率相等,并且在下面的章节中说明一个排列的生成过程时也省略了下标 $π$。给定一个排列顺序,我们可以将对数似然率自动回归分解-每次迭代生成一个节点,如下所示:
在第i步,使用所有 i 之前已生成的节点,他们的属性和边分别是 $X{\lt i}$ ,$E{\lt i}$ ,给定 $X{\lt i}$ $E{\lt i}$ 生成节点 i 的概率log加和。
从本质上讲,等式中的目标。描述了属性图的自回归生成过程。问题变成:如何对条件概率 $pθ(X_i,E_i|X{<i},E_{<i})$ 建模?
因式分解属性图生成
为了计算 $p{\theta}(X_i,E_i|X{\lt i},E_{\lt i})$ ,一种天真的解决方案可以是简单地假设 $X_i$ 和 $E_i$是独立的,即 :
然而通过这样的分解,对于每个节点,其属性和连接之间的依赖性被完全忽略。
然而,被忽略的依赖性是属性图的核心性质,也是GNNs中卷积聚集的基础。因此,这种天真的分解不能为训练前的GNN提供信息指导。
就比如,物以类聚人以群分,我和相似的人右边是因为我们有相似的属性。
为了解决这个问题,作者提出了属性图生成过程的依赖感知分解机制。具体地说,当估计一个新节点的属性时,我们会得到它的结构信息,反之当估计一个新的结构边信息时,我们会考虑到它的属性信息。在该过程中,可以将生成分解为两个耦合部分:
- 1.给出观测边的边,生成节点属性
- 2.给出观测边和1中已经生成的节点属性,生成剩余的边
通过这种方式,模型可以捕获每个节点的属性和结构之间的依赖关系。
正式的定义如何建模,定义一个变量 $o$ , 表示$E_i$内所有观测边的索引向量。
$E_{i,o}$ 是已观测的边,$\lnot o$表示要生成的所有mask边的索引。通过所有的已观测边来重写条件概率作为一个期望似然如下:
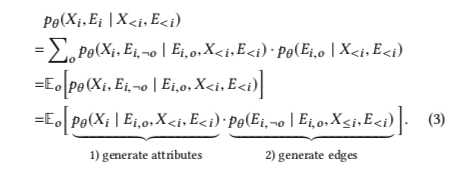
这里的理解非常重要,第一个等式中,把 $Ei$ 拆成了$E{i,¬o}$和 $E_{i,o}$ ,也就是说指定了哪些边是观测边,哪些边是masked边。需要注意的是,当o确定下来了,$\lnot o$ 也是确定的。因此等式外面加上了对o的累加,这里可以理解为类似于全概率公司去对所有可能的o求和。
此外,这里要注意 $Ei, E{<i},E{i,o},E{i,\lnot o}$ 四个符号分别表示什么:
- 现在位于step i,$E_{<i}$ 是指在step i 之前生成的边
- $E_i$ 指在step i 将会生成的边 (与节点i 相连,有好多边)
- 将 $Ei$ 的边生成过程拆分成一件生成的和将要生成的两部分,即 $E{i,o},E_{i,\lnot o}$
在第二个等式中,把p 看成是概率分布,写作对于o 期望的形式。
最后把 $Xi$ 和 $E{i,\lnot o}$ 看做独立的过程,拆成两个概率分布。
这种分解的优势在于,没有忽略 $Xi$ 和 $E{i,o}$ 的联系。第一项表示given观测边,聚合目标节点i的邻居信息来生成其属性$Xi$ 。第二项表示given观测边和刚生成的属性$X_i$,预测$E{i,¬o}$中的边是否存在。
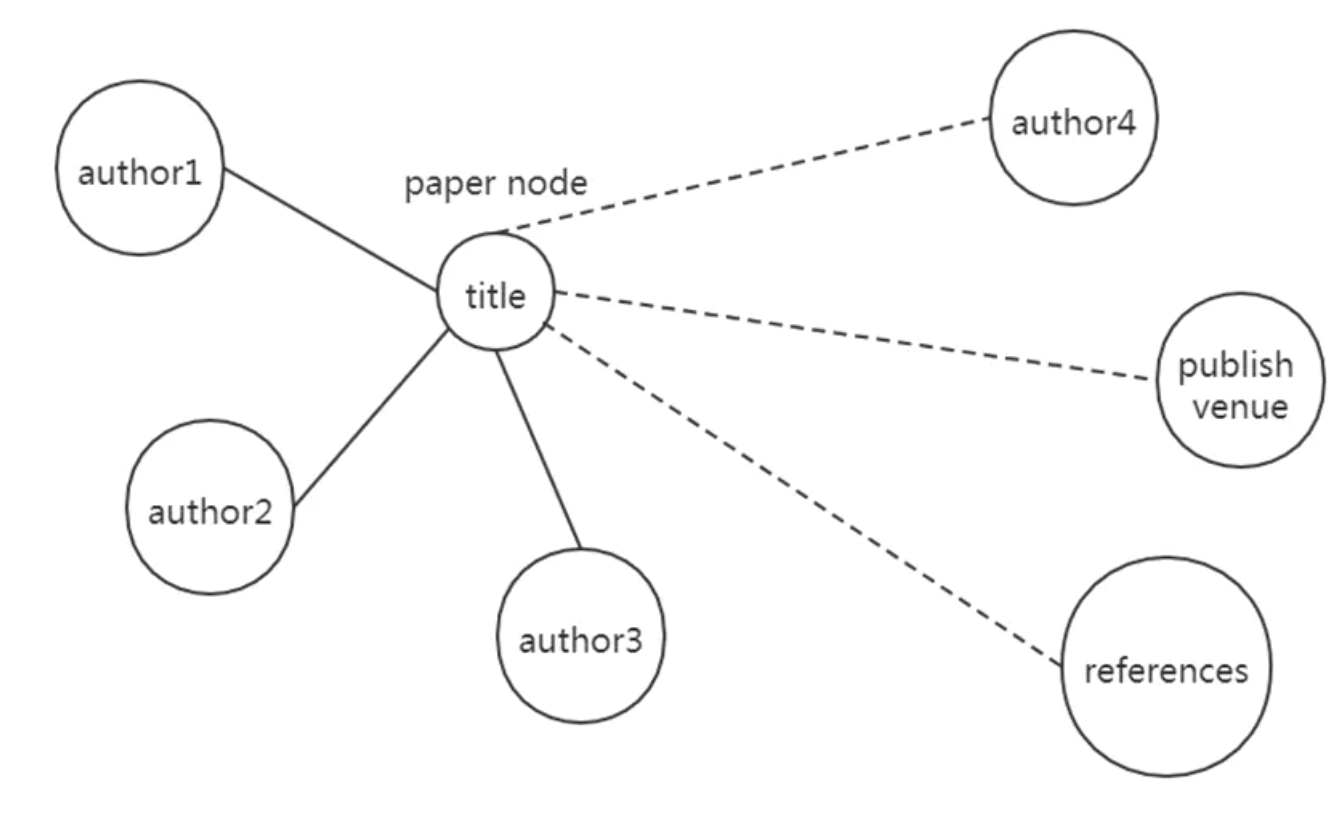
如上图所示,给出一个例子。对于academic图,我们要去生成一个paper node,它的属性为title。我们要去生成一个paper node,它的属性为title,并且其和author,publish venue,reference相连。上图中的实线部分为已经观测到的边,首先生成节点的属性,即title。然后基于author1,author2,author3和刚生成的节点属性title,预测剩下的边,即虚线部分。
高效的属性和边生成
出于效率考虑希望:
- 对于输入图只跑一次GNN就能计算节点属性生成和边生成过程的loss
- 希望节点属性生成和边生成能同时运行
然而边生成需要用到节点属性信息,如果两个生成过程同时进行,会导致信息泄露。为避免这个问题,将节点分成两种类型:
- 属性生成节点,mask住这些节点的属性,用一个公用的dummy token,并学习一个共享向量$X^{init}$来代替 和$X_i$ 维度相同。
- 边生成节点,对于这些节点,保留他们的属性。
需要注意的是,同一个节点在不同阶段扮演不同的角色,可能是属性生成节点也可能是边生成节点。只在某一阶段,一个节点有一个确定的角色。
在graph上训练GNN 来生成各个节点的embedding,用$h{attr}$ 和 $h{edge}$ 来分别表示属性生成节点和边生成节点的embedding。由于属性生成节点的属性被mask了,因此$h{attr}$中包含的信息通畅会少于 $h{edge}$。
因此,在GNN的message passing过程中,只使用$h_{edge}$ 作为向其他节点发送的信息。 也就是说,对于每个节点,其聚合邻居 $h_edge$ 的信息和自身信息来生成新的embedding。之后使用不同的decoder来生成节点属性和边。(注意,节点的embedding和节点属性不是一回事。通俗理解,在GNN中节点的属性是input,节点的embedding是hidden layer。)
对于属性生成,用$Dec^{Attr}(\cdot)$ 来表示decoder,输入$h_{attr}$ 来生成节点属性。decoder的选择依赖于节点属性的类型,如果是text类型的节点属性,可以使用LSTM等。如果节点属性是vector,可以使用MLP。
定义一个距离函数来度量生成属性和真实属性之间的差异,对于text类型属性,可以使用perplexity困惑度,对于vector属性,可以使用L2距离。因此,可以计算属性生成过程中的loss
最小化生成属性和真实属性之间的差异,等价于对generate attribute做MLE,也就是最大化 $p{\theta}(X_i|E{i,o},X{<i},E{<i})$ 从而捕捉了图中的节点属性信息。
对于边生成过程,假设每条边的生成过程和其他边是独立的,由此对likelihood分解:
得到$h_{edge}$ 后,如果节点i和节点j相连,则使用
进行建模,$Dec^{Edge}$ 是一个pairwise score function
loss定义为:
$S_i^-$ 是指没有和节点i相连的节点
下面是作者给出的属性图生成过程的说明性示例。
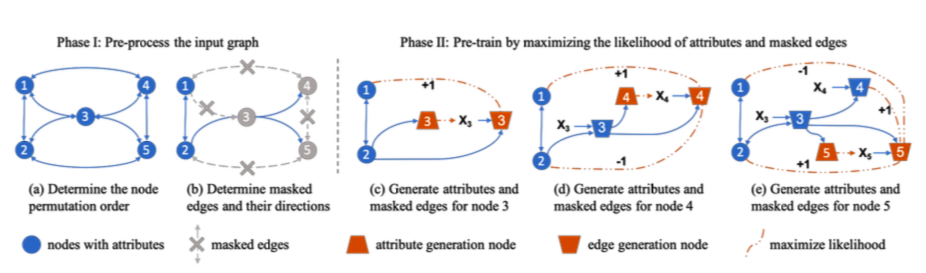
- a) 对于input graph 确定排列 $\pi$
- b) 随机挑选一部分与节点i相连的边作为已观测的$E{i,o}$ ,剩下的作为masked edges $E{i,\lnot o}$ 并删除masked edges
- c) 把节点分为属性生成节点和边生成节点
- d) 计算节点 3,4,5的embedding,包括他们的属性生成节点和边生成节点。
- d)-e) 通过对每个节点并行进行节点属性预测和masked预测来训练一个GNN模型
具体算法流程:

输入一个属性图,每次采样一个子图 $\hat G$作为训练的实例进行训练。首先决定permutation order π。同时,我们希望能够并行化训练,只做一次前向传播,就能得到整个图的embedding,由此可以同时计算所有节点的loss。因此,根据permutation order π来移除边,也就是使每个节点只能从更低order的节点处获得信息。
之后,需要决定哪些边被mask。对于每个节点,获得其所有的出边,随机挑选一部分边被mask住,这一过程对应上述line4。
之后,对节点进行划分,得到整个图中节点的embedding,用于之后loss的计算,对应line5。
line 7-9进行loss的计算。
line 8中,通过整合采样图中未连接的节点和Q中以前计算的节点embedding来选择负样本,这种方式能够减轻对于采样图优化和对于整个图优化的差距。
在line11-12中,优化模型并更新Q。
GPT-GNN 对于异质的大图
对于异构图,即包含不同类型的点和边的图,唯一的不同在于不同类型的点和边采用不同的decoder。
对于大规模的图,可以采样子图来进行训练,即上述算法流程中Sampler的作用。为了计算 $L_{edge}$ 这一loss,需要遍历输入图的所有节点。然而,我们只能在采样的子图上计算这个loss。为了缓解这一差异,提出了adaptive queue,其中存储了之前采样的子图的节点embedding作为负样本。每次采样一个新的子图时,逐步更新这个队列,增加新的节点embedding,移除旧的节点embedding。通过引入adaptive queue,不同采样子图中的节点也能为全局的结构提供信息。
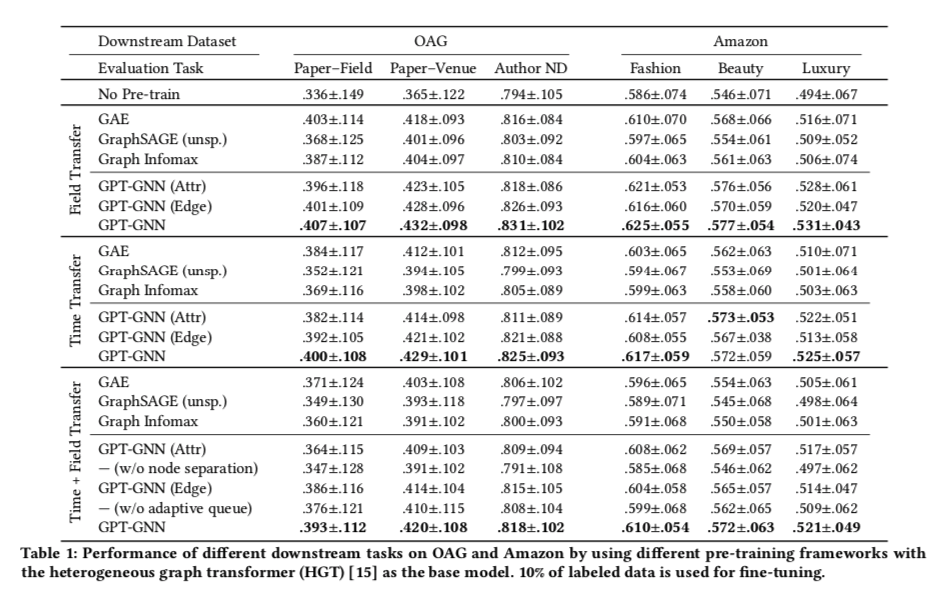
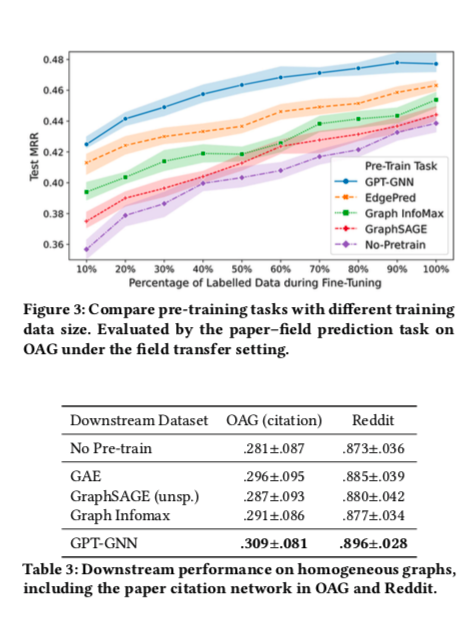
实验效果