Learning to Pre-train Graph Neural Networks

动机与挑战

图神经网络也是有预训练模型的，预训练之所以可以提升，可以解释为获取了有用的先验知识，并迁移到任务中。

常规的GNN预训练步骤和其他网络一样分为两个步骤：

在大量未标记的图数据上预先训练GNN模型，其导出编码固有图属性的通用可转移知识
在特定于任务的图形数据上对预先训练的GNN模型进行微调，以使通用知识适用于下游任务。

但之前有人已经研究过直接进行fine-tuning效果不提反降，产生负迁移效果。应该是出自(Strategies for Pre-training Graph Neural Networks 如何解决的以后看了这篇论文再说)

而这篇文章的主要想解决的是由于预训练和fine-tuning优化目标的不同，两者之间存在明显差距，损害了模型的泛化效果。

引出了第一个挑战：如何缩小不同优化目标带来的差距？ —->>元学习思想

那GNN的预训练模型的特点是不仅要考虑局部的节点级先验知识还要获取图级别的全局先验知识 (现有方法要么只考虑节点级的预训练，或者仍然需要用有监督的图级预训练)

引出了第二个挑战：如何利用完全未标记的图数据同时保留节点级和图形级信息？

提出了L2P-GNN，计了节点级和图级的双重自适应机制，并且是完全自监督的方式。

设计

GNN

首先定义一个图 $G = (V,E,X,Z)$ , 其中 $V$ 是节点、$E$ 是边、$X \in R ^{|V|\times d_v}$ 是节点特征、 $Z \in R^{|E|\times d_e}$ 是边的特征。

GNN 一般包含两个关键的计算，一个是聚合信息的操作AGGREGATE，另一个是更新操作UPDATE

节点表示：节点v的l层表示由下式给出：

$\begin{equation}\begin{split} h_v^l &= \Psi (\psi, A, X,Z)^l\\ &= \text{UPDATAE}(h_v^{l-1}, AGGREGATE(\{(h_v^{l-1}, h_u^{l-1}, z_{uv}): u\in N_v\})) \end{split}\end{equation}$

其中 $z_{uv}$ 是u到v的边特征向量，A是邻接矩阵，$N_v$ 是v的邻居节点。$\Psi$ 是聚合和更新操作的定义，$\psi$ 是可学习参数。

图级的表示：通常用READOUT

$\begin{equation}\begin{split} h_G = \Omega(w ; H^l) = \text{READOUT} (\{h_v^l| v\in V\}) \end{split}\end{equation}$

其中$H^l = [h_v^l]$ 是节点级表达矩阵。READOUT的典型实现有sum、max、mean池化，或者用其他复杂一点的方法。

常规GNN的预训练

预训练：定义 $D^{pre}$ 为预训练图数据，$L^{pre}$ 预训练的loss ，优化目标为：

$\theta_0 = argmin_{\theta} L^{pre} (f_\theta; D^{pre})$

fine-tuning：目标是，在对下游任务的训练集图数据$D^{tr}$进行微调之后，最大化下游测试集图数据$D^{te}$上的表现

所谓的微调根据预先训练的参数$\theta0$来初始化模型，并且用在(通常是批处理的)$D{tr}$上的多步梯度下降来更新GNN模型 $f_{\theta}$。

$\theta_1 = \theta_0 - \eta ▽_{\theta_0} L^{fine}(f_{\theta_0};D^{tr})$

其中 $ \eta$ 学习率

可见常规的预训练和finetuing是解耦的，参数$\theta_0$ 和下游没有适应性的联系形式。

为此，作者提出通过构建预训练阶段来模拟下游任务的微调过程，从而直接优化预训练模型对下游任务的快速适应性。

新的预训练方法

其实就是元学习的思想参考上文 Meta Learning(李宏毅)

现有$G\in D^{pre}$ 从中采样一些子图定义为$D^{tr}{T_G}$ 作为模拟下游任务$T_G$的训练数据——元学习中的support sets，再采样一些子图作为$D^{te}{T_G}$ 作为模拟的验证集——元学习中的query sets。

$\theta_0 = argmin_{\theta} \sum_{G\in D^{pre}} L^{pre}(f_{\theta - \alpha ▽_{\theta}L^{pre}(f_{\theta}; D^{tr}_{T_G})}; D^{te}_{T_G})$

$\theta - \alpha ▽{\theta}L^{pre}(f{\theta}; D^{tr}{T_G})$ 相当于在$D^{tr}{T_G}$ 预训练的测试集先进行了一次fine-tuning

作者认为：因此，预培训输出$θ_0$并不是为了直接优化任何特定任务的训练或测试数据。相反，θ0通常是最佳的，因为它允许快速适应新任务。

我认为：这类似元学习的思想，还可以从元知识的角度来描述。还有一个点，这个预训练数据集和下游任务相不相关呢？如果相关度不大会不会有用，如果相关会不会更好？

L2P_GNN

两个特点：

从局部和全局角度捕捉图形中的结构和属性
套用MAML获得元学习的先验知识可以适应新的任务或图表

任务实施

定义每个任务的图数据随机采样得到 $T_G = (S_G,Q_G)$ , $S_G$ 为Support set ，$Q_G$ 为Query set

多个任务的支持集合查询集为: $S_G =(S_G^1,S_G^2,…,S_G^k) ,Q_G =(Q_G^1,Q_G^2,…,Q_G^k)$

在给定父任务和子任务的情况下，作者设计了一个节点级聚集和图级汇集的自监督基本GNN模型，分别学习节点和图的表示。其核心思想是利用无标签图数据的内在结构作为节点级和图级的自我监督。

节点级：自监督预测u和v节点有边链接的目标函数

$L^{node}(\psi;S_G^c) = \sum_{(u,v)\in S_G^e} -ln(\sigma(h_u^Th_v)) -ln(\sigma(-h_u^Th_{v'}))$

其中 $v’$ 是负采样节点，是没有和u有边的节点。

图级：通过图池化获得图表达$hG$，每个任务的支持集图表达为 $h{S_G^c} = \Omega(w;{h_u|\forall u,\exists v:(u,v) \in S_G^c})$

$L^{graph} (w; S_G) = \sum_{c=1}^k -log(\sigma(h_{S_G^c}^T h_G)) -log(\sigma(-h^T_{S_G^c}h_{G'}))$

两个级别的loss综合到一起：

$L_{T_G}(\theta;S_G) = L^{graph}(w;S_G) + \frac{1}{k} \sum_{c=1}^k L^{node}(\psi;S_G^c)$

其中$\theta = {\psi,w}$ 是可学习参数，就是可迁移的先验知识

双重适应(图级和节点级)

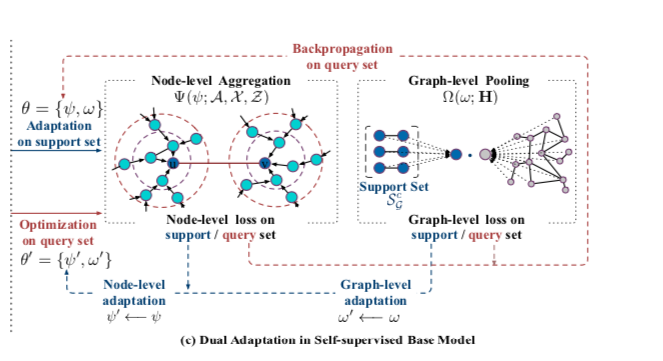
节点级：支持loss采用一个或几个梯度下降步骤，以获得子任务的适应先验 $ψ$。例如，当使用一个具有节点级学习率$α$的梯度更新时:

$\psi' = \psi - \alpha \frac{\partial\sum_{c=1}^k L^{node}(\psi;S_G^c)}{\partial\psi}$

图级：

$w' = \psi - \beta \frac{\partial L^{graph}(w;S_G^c)}{\partial w}$

所有任务的更新参数过程

$\theta \gets \theta - \gamma\frac{\partial\sum_{G\in D^{pre}}L_{T_G}(\theta';Q_G) }{\partial \theta}$

实验

实验的主要目的：要验证有没有缩小预训练和微调的gap图级和节点级预训练策略是否奏效

作者对预训练的GNN模型在下游任务微调前后（命名为model-P和model-F）进行了对比分析，并考虑了三个比较视角：model-P和model-F参数之间的中心核对齐相似性（CKA），训练损失（delta损失）和下游任务测试性能（delta RUC-AUC或Micro-F1）的变化。

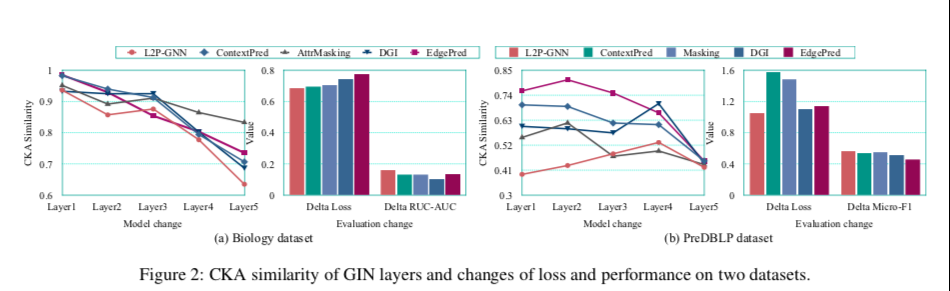
如图所示，观察到L2P-GNN参数在微调前后的CKA相似性通常比基线的CKA相似性小，这表明L2P-GNN经历了更大的变化，以便更好地适应下游任务。

CKA 是测量神经网络表示相似性的，可以对迁移学习任务进行评估，值越小越相似。

此外，L2P-GNN的训练损失变化较小，说明L2P-GNN通过快速适应可以很容易地达到新任务的最优点。

参考

GNN预训练的论文

Hu, W.; Liu, B.; Gomes, J.; Zitnik, M.; Liang, P.; Pande, V. S.; and Leskovec, J. 2020. Strategies for Pre-training Graph Neural Networks. In Proceedings of ICLR.

Hu, Z.; Fan, C.; Chen, T.; Chang, K.; and Sun, Y. 2019. Pre-Training Graph Neural Networks for Generic Structural Feature Extraction. CoRR abs/1905.13728.

Navarin, N.; Tran, D. V.; and Sperduti, A. 2018. Pre-training Graph Neural Networks with Kernels. CoRR abs/1811.06930.

元学习

Finn, C.; Abbeel, P.; and Levine, S. 2017. Model-agnostic meta-learning for fast adaptation of deep networks. In Pro- ceedings of ICML, 1126–1135.

Lu, Y.; Fang, Y.; and Shi, C. 2020. Meta-learning on Hetero- geneous Information Networks for Cold-start Recommenda- tion. In Proceedings of KDD, 1563–1573.