DP分析法—01背包问题
从集合角度来分析DP问题,DP问题的题目一般都是从有限集中求得最值的问题。
01背包问题
有 N 件物品和一个容量是 V 的背包。每件物品只能使用一次。
第 i 件物品的体积是 $v_i$,价值是 $w_i$。
求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。
输出最大价值。
输入格式
第一行两个整数,N,V,用空格隔开,分别表示物品数量和背包容积。
接下来有 N 行,每行两个整数 $v_i,w_i$,用空格隔开,分别表示第 i 件物品的体积和价值。
输出格式
输出一个整数,表示最大价值。
数据范围
0<N,V≤10000<N,V≤1000
0<vi,wi≤10000<vi,wi≤1000
输入样例
输出样例:
解
最多$2^N$, 从$2^N$ 个方案里找总价值最大的方案。——有限集合的最值问题
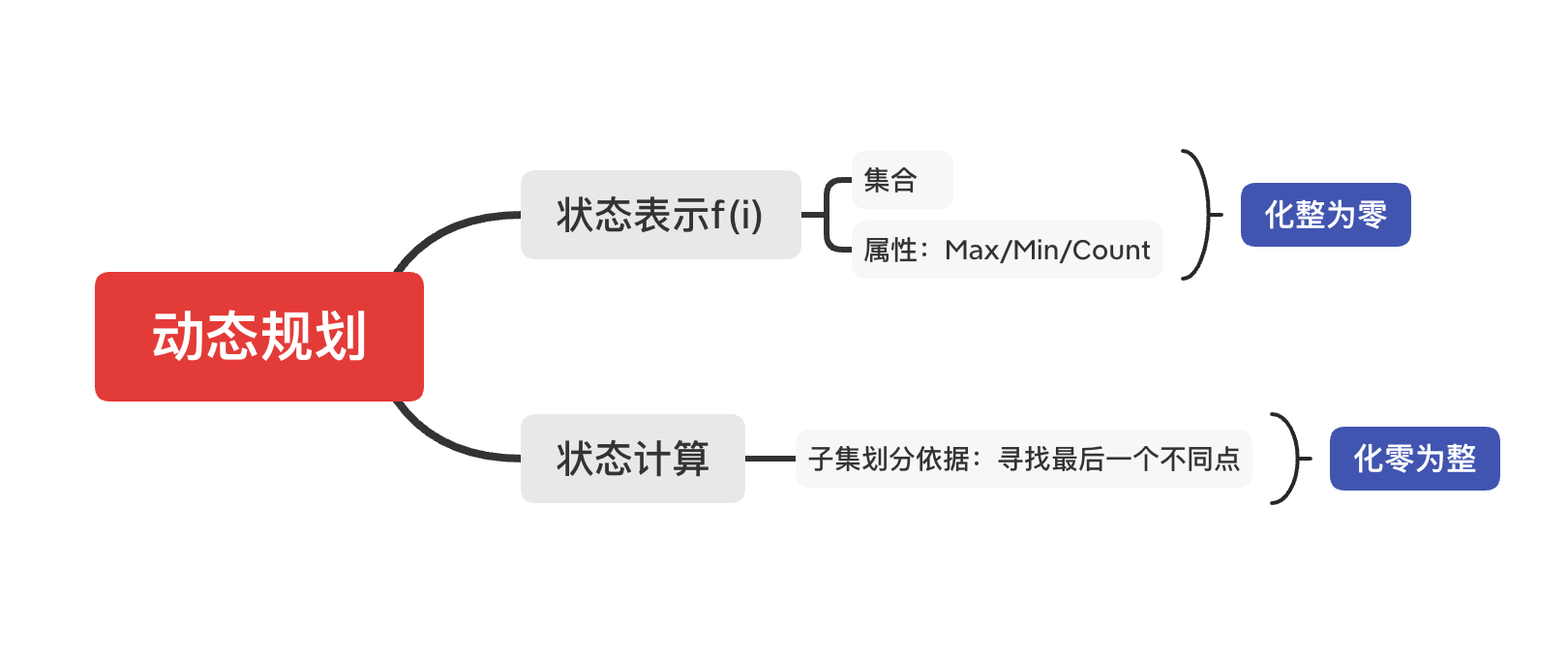
状态表示:
选择问题一般$f(i,j)$ 第一维表示前i个物品,第二维是限制 (经验)
集合:所有只考虑前i个物品,且总体积不超过j的选法的集合。
- 属性:集合中每一个方案的最大价值Max
状态计算:
- 所有不选第i个物品的方案 $f(i-1,j)$
- 所有选择第i个物品的方案 $f(i-1,j-v_i) + w_i$
- $Max(f(i-1,j), f(i-1,j-v_i)+w_i)$
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
| import java.util.Scanner;
public class Main{
public static void main(String[] args) throws Exception {
Scanner reader = new Scanner(System.in);
int N = reader.nextInt();
int V = reader.nextInt();
int[] v = new int[N + 1] ;
int[] w = new int[N + 1] ;
for (int i=1 ; i <= N ; i++){
v[i] = reader.nextInt();
w[i] = reader.nextInt();
}
reader.close() ;
int[][] dp = new int[N+1][V+1];
dp[0][0] = 0;
for(int i = 1; i <= N; i++){
for(int j = 0; j <= V; j++){
if(j >= v[i]){
dp[i][j] = Math.max(dp[i-1][j], dp[i-1][j-v[i]] + w[i]);
}else{
dp[i][j] = dp[i-1][j];
}
}
}
System.out.println(dp[N][V]);
}
}
|
优化后
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
| import java.util.Scanner;
public class Main{
public static void main(String[] args) throws Exception {
Scanner reader = new Scanner(System.in);
int N = reader.nextInt();
int V = reader.nextInt();
int[] v = new int[N + 1] ;
int[] w = new int[N + 1] ;
for (int i=1 ; i <= N ; i++){
v[i] = reader.nextInt();
w[i] = reader.nextInt();
}
reader.close() ;
int[] dp = new int[V+1];
dp[0] = 0;
for(int i = 1; i <= N; i++){
for(int j = V; j >= v[i]; j--){
dp[j] = Math.max(dp[j], dp[j-v[i]] + w[i]);
}
}
System.out.println(dp[V]);
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
| public static int o1bagSolutionOptimization(int[] weight, int[] value, int bagWeight) {
int num = weight.length;
int[] dp = new int[bagWeight + 1];
dp[0] = 0;
for (int i = 1; i <= num; i++) {
for (int j = bagWeight; j >= 1; j--) {
if (j >= weight[i - 1]) {
dp[j] = Math.max(dp[j], dp[j - weight[i - 1]] + value[i - 1]);
}
}
}
return dp[bagWeight];
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int itemsNumber = sc.nextInt();
int bagWeight = sc.nextInt();
int[][] arr = new int[itemsNumber][2];
int[] weight = new int[itemsNumber];
int[] value = new int[itemsNumber];
for(int i = 0; i < itemsNumber; i++) {
for(int j = 0; j < 2; j++) {
arr[i][j] = sc.nextInt();
}
weight[i] = arr[i][0];
value[i]= arr[i][1];
}
System.out.println(o1bagSolutionOptimization(weight, value, bagWeight));
}
|
完全背包问题
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
| public class 完全背包问题 {
public static void main(String[] args) throws Exception {
Scanner reader = new Scanner(System.in);
int N = reader.nextInt();
int V = reader.nextInt();
int[] v = new int[N + 1];
int[] w = new int[N + 1];
for (int i = 1; i <= N; i++) {
v[i] = reader.nextInt();
w[i] = reader.nextInt();
}
reader.close();
int[] dp = new int[V + 1];
dp[0] = 0;
for (int i = 1; i <= N; i++) {
for (int j = 0; j <= V; j++) {
if (j >= v[i]) {
dp[j] = Math.max(dp[j], dp[j - v[i]] + w[i]);
}
}
}
System.out.println(dp[V]);
}
}
|