10-正则表达式

10. 正则表达式匹配

定义状态

  • 定义动态数组$dp[m][n]$ （n为字符串p的长度+1，m为字符串s的长度+1）
    • 为什么要加1
    • 因为我们还要处理空字符串的情况，比如p为空，s为空，或者p为空，s不为空
  • $dp[m][n]$ 的含义：p的前$n-1$ 个字符能否匹配s的前$m-1$个字符
    • 为什么是n-1和m-1?
    • 因为动态数组里面加了一列和一行空字符的匹配情况，故需要-1才能对应相应字符串

因此创建好的dp数组如下图：

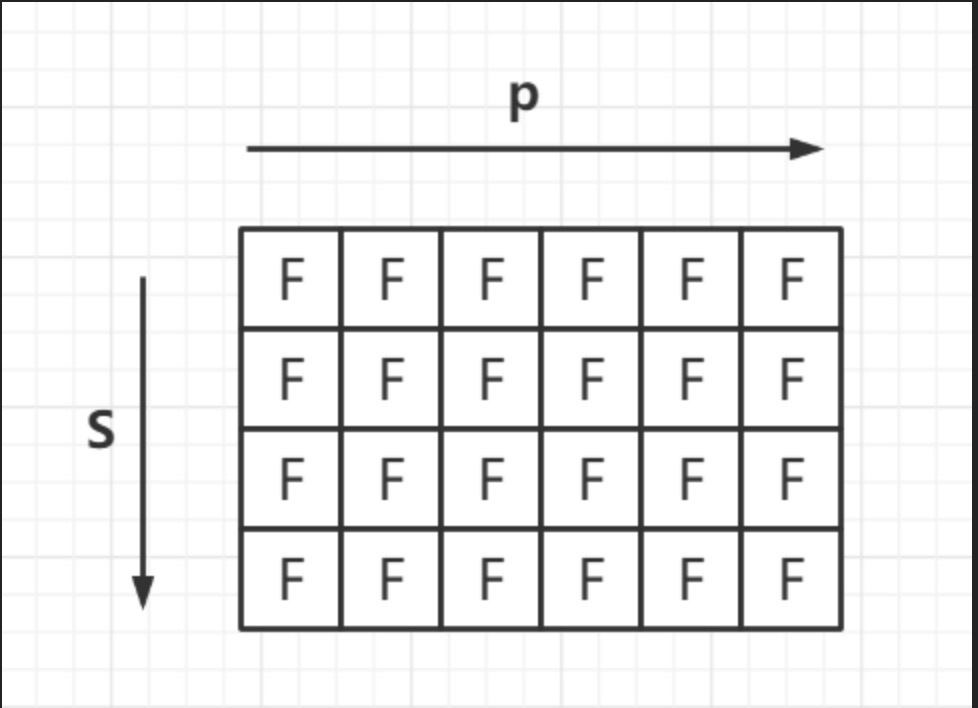
确定动态转移方程

说明：为了区别dp数组与字符串索引的区别(因为相差1)，我们设 $i=r-1,j=c-1$ （r为dp里面的行索引，c为dp里面的列索引）

有以下几种情况是需要我们处理的：

  • 当 $s[i]=p[j] \ || \ p[j]==’.’$ （即正好能够匹配或者相对应的是一个 $.$）

那么我们只需要看一下前面 $dp[r-1][c-1]$的状态，$dp[r][c]$继续延续即可

即状态转移方程为 $dp[r][c]=dp[r-1][c-1]$

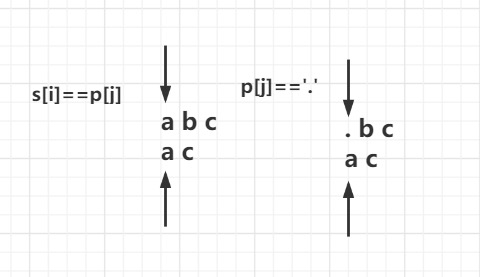
  • 当 $p[j] ==’‘$ （即匹配到了万能字符 $$）

    两种情况分别对应的处理方式为：

    如果 $*$ 的前一个字符正好对应了$s$，状态转移过程为：$dp[r][c] = dp[r-1][c]$

    如果是$*$的前一个字符为 $.$ 那么只需看$.$的前面字符匹配情况，状态转移过程为: $dp[r][c]=dp[r][c-2]$

边界：

  • 首先我们要确定 $dp[0][0]$，当p为空，s为空时，肯定匹配成功。那么$dp[0][0]=true$

  • 当 p 为空字符串，而s不为空时，dp数组必定为False，正好初始化dp数组的时候设置的是False；即dp数组的第一列为False可以确定

  • 当s为空字符串，而p不为空时，我们无需判断p里面的第一个值是否为””，如果为””,那肯定匹配不到为Fasle,原数组正好是Fasle，所以直接从2开始判断即可。如果遇到了*,只要判断其对应的前面两个元素的dp值

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
class Solution {
    public boolean isMatch(String s, String p) {
        int n = s.length();
        int m = p.length();
        boolean[][] dp=new boolean[n+1][m+1];
        s = ' '+s;
        p = ' '+p;
        dp[0][0] = true;

        for(int i=0;i<=n;i++){
            for(int j=0;j<=m;j++){
                if(i==0 && j==0) continue;
                if(p.charAt(j) != '*'){
                    if(p.charAt(j)=='.' || s.charAt(i)==p.charAt(j)){
                        if(i>0 && j>0){
                            dp[i][j] = dp[i-1][j-1];
                        }
                    }
                } else{
                    if(j>=2) dp[i][j] = dp[i][j-2];
                    if(i>0 && j>0){
                        if(p.charAt(j-1) == '.' || s.charAt(i)==p.charAt(j-1)){
                            if(dp[i-1][j]) dp[i][j]=true;
                        }
                    }
                }
            }
        }
        return dp[n][m];
    }
    
  }