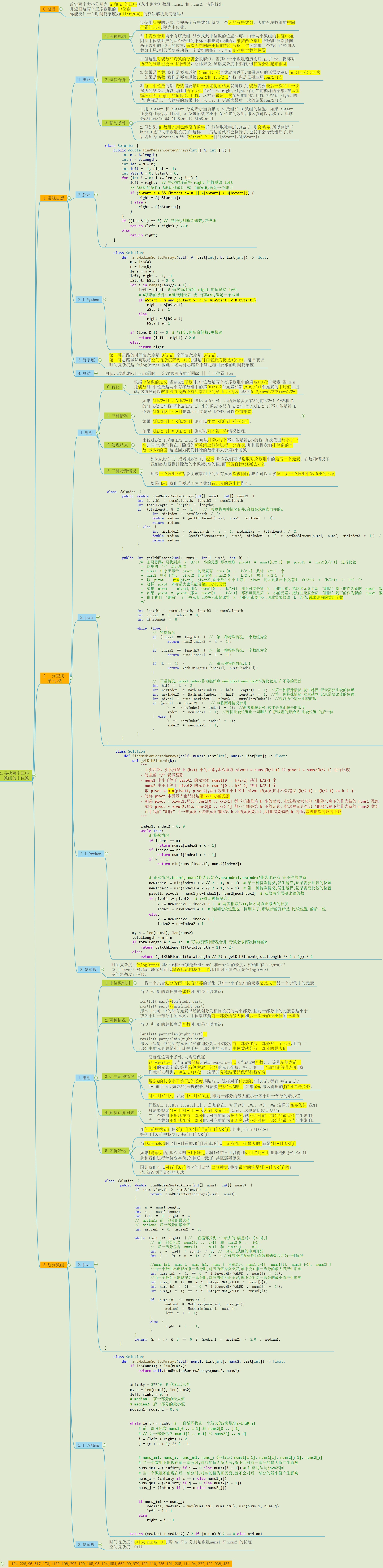
4-三种方法彻底解决中位数问题
4. 寻找两个正序数组的中位数
两种思想
- 真合并:使用归并的方式,合并两个有序数组,得到一个大的有序数组,大的有序数组中的中间位置的元素即为中位数。$O(n+m),O(n+m)$
- 假合并:不需要合并两个有序数组,只要找到中位数的位置即可。由于两个数组的长度已知,因此中位数对应的两个数组下标之和也是已知的。维护两个指针,初始时分别指向两个数组的下标为0的位置,每次将指向较小的指针后移一位(如果一个指针已经到达数组末尾,则只需要移动另一个数组的指针),直到达到中位数的位置。$O(n+m),O(1)$
常见的思想改进:假合并、奇偶合并
通过假合并的思想可以将空间复杂度优化到$O(1)$但对于时间复杂度并没有什么优化,此方法代码复杂,不仅要考虑奇偶问题,更需要高了一个数组遍历后的各种边界问题。
假合并的一个优化点是 将奇偶两种情况合并到了一起:
- 如果是奇数,我们需要知道第(len+1)/2 个数就可以了,如果遍历的话需要遍历int(len/2)+1次
- 如果是偶数,需要知道第(len/2) 和 len/2 + 1个数,也是需要遍历len/2 + 1次
- 返回中位数,奇数需要最后一次遍历结果就可以,偶数需要最后一次和上一次的结果。所以用两个变量left和right。right保存当前循环的结果,在每次循环前将right赋值给left。这样在最后一次循环的时候,left将得到right的值,也就是上一次的循环结果,加下来right更新为最后一次的结果len/2+1次
另一种合并的思想是: 我们可以在奇数的时候, 在末尾等处添加一个占位符#等, 这样也是可以将奇数合并成偶数的情况的.此方法的另一个优化点就是 通过在if条件中加入大量的限制条件, 从而实现了对于各种边界问题的处理, 这也是一种很重要的思想.

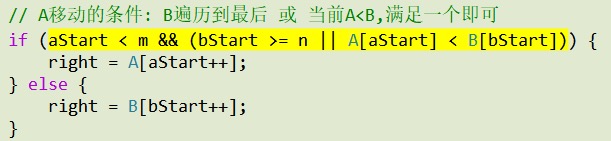
此方法的时间复杂度相对于下面两种思想还是太高了, 大家不用特意掌握此方法, 但是这两个优化的思想还是很重要的, 要好好的理解一下.
接下来我们就来详细讲解两个时间复杂度超低的算法代码思想.
寻找第k小数(记住这个)
主要就是根据两个数的三种比较结果, 不断地去除不满足的元素的过程.

这个思想最难的点在于 三种特殊情况的处理, 我们能否想到这三种情况, 并将他们完美的融入到代码之中, 我感觉这才是真正的难点所在.

最开始对于奇数和偶数的两种情况进行了判断, 其实是可以将两种情况合并的, 只需要在奇数时求两次同样的k就可以了.

接下来处理了三种特殊情况中的两种特殊情况: 一个数组为空 和 k=1.

下面的几个定义就非常重要了, 一定要弄清这些定义的含义, 才能更轻松的理解代码.
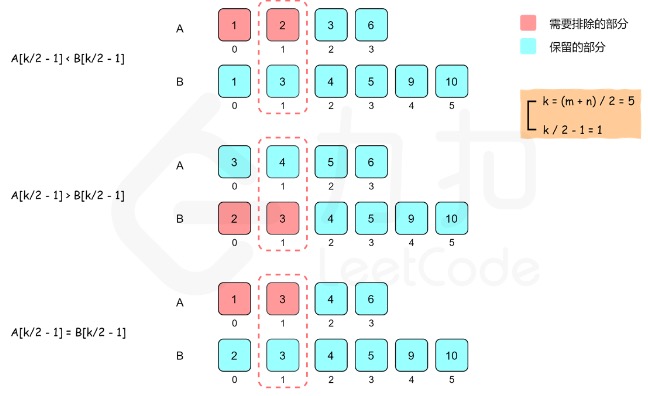
index1, index2作为数组的起始点的下标, 初值都是0, 但是随着两个数组不断被删除元素, 这两个起始点也是在不断的进行变化, 具体变化方式就是 index1 = newIndex1 + 1, 因为在删除元素的时候 连同比较位置也一同删去了, 所以新的开始是 比较位置 的后一位.
newindex1, newindex2作为比较点就是图中被框中的两个数的下标, 它的赋值过程就涉及到了 最后一个边界情况. 因为当一个数组较短时, 其中一个比较点可能已经到达了数组的最后, 所以它的值是 两种情况下较小的那个数.

接下来就是根据两个比较点的大小来进行不同的操作过程了, 这里最难理解的点就是 k -= (newIndex1 - index1 + 1), 也就是减去元素的个数问题了. 我们根据上面的图来举例, 图中index1的值为0, newindex1的值经过计算为1, 通过比较后, 可以看到 红色的数 就是被删除的数, 也就是两个, 所以我们需要在最后+1才是真实被删去的个数. 对于此类问题在确定最终个数的时候, 我们都可以通过这样的特例来决定代码的书写, 至此代码就全部讲解完成了.

理解中位数作用进行划分数组
最后这种思想时间复杂度比上面的还低,上面的思想每一轮循环可以将查找范围减少一半,因此时间复杂度是$O(log(m+n))$ ,但这种思想可以对确定的较短的数组进行二分查找,所以它的时间复杂度是$O(logmin(m,n))$
划分数组正好和上面算法完全相反,它的思想特别复杂,但思想理解了,代码写起来倒是没太大难度。
首先要明白中位数的作用:将一个集合划分为两个长度相等的子集,其中一个子集中的元素总是大于另一个子集中的元素。这种思想无论是在机构数组中都是适用的,这就衍生出了下面的思想。
首先讨论奇偶两种不同情况的不同划分方式,
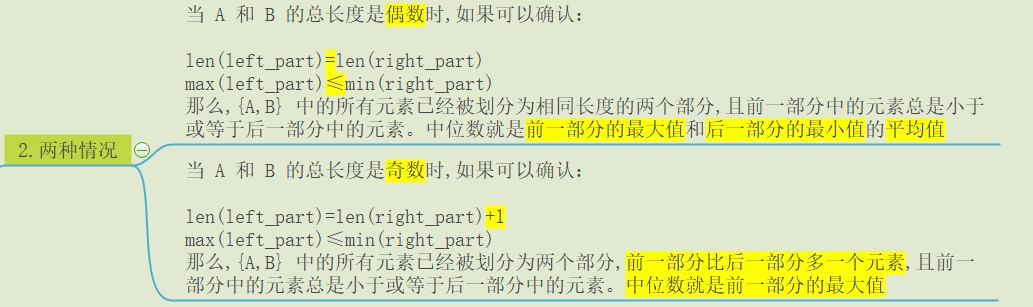
然后在写代码时,由于计算机的取整操作,我们是可以将这两种情况合并成一种代码书写方式,其中的$i$和$j$分别是两个数组的划分位置。

同样我们也会遇到复杂的边界问题, 但下面这种处理方式是真的非常优秀.

上面问题都考虑完了, 其实就可以写代码了, 但是我们需要进行两个条件的判断: B[j−1]≤A[i] 以及A[i−1]≤B[j], 为了优化代码, 经过分析后, 我们发现这两种情况是可以等价转换的. 也就是只需要进行一个条件的判断即可.

代码中有个注意点就是java中的三目运算符? : 在Python中是没有引入这个符号的, 但是Python利用了已有的关键字if…else实现了这个功能.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
| class Solution {
public double findMedianSortedArrays(int[] nums1, int[] nums2) {
int m = nums1.length;
int n = nums2.length;
int len = m+n;
int left = -1, right= -1;
int aStart=0, bStart=0;
for(int i=0;i<=len/2;i++){
left = right;
if(aStart < m && (bStart>=n || nums1[aStart] < nums2[bStart])){
right = nums1[aStart++];
}else{
right= nums2[bStart++];
}
}
if((len & 1) == 0)
return (left+right)/2.0;
else
return right;
}
public double findMedianSortedArrays(int[] nums1, int[] nums2) {
int length1 = nums1.length;
int length2 = nums2.length;
int totallength = length1+ length2;
if(totallength % 2 == 1){
int midIndex = totallength/2;
double median = getKthElement(nums1, nums2, midIndex+1);
return median;
} else{
int midIndex1 = totallength/2 -1 , midIndex2 = totallength/2;
double median = (getKthElement(nums1, nums2, midIndex1 + 1) + getKthElement(nums1, nums2, midIndex2 + 1)) / 2.0;
return median;
}
}
public int getKthElement(int[] nums1, int[] nums2, int k){
int length1 = nums1.length, length2=nums2.length;
int index1 = 0, index2=0;
int kthElemnt=0;
while(true){
if(index1==length1){
return nums2[index2+k-1];
}
if(index2==length2){
return nums1[index1+k-1];
}
if(k==1){
return Math.min(nums1[index1], nums2[index2]);
}
int half = k/2;
int newIndex1 = Math.min(index1 + half, length1) -1;
int newIndex2 = Math.min(index2 + half, length2) - 1;
int pivot1 = nums1[newIndex1], pivot2=nums2[newIndex2];
if(pivot1<=pivot2){
k -= (newIndex1 -index1 +1);
index1 = newIndex1+1;
} else{
k -= (newIndex2-index2+1);
index2 = newIndex2+1;
}
}
}
public double findMedianSortedArrays(int[] nums1, int[] nums2) {
if (nums1.length > nums2.length) {
return findMedianSortedArrays(nums2, nums1);
}
int m = nums1.length;
int n = nums2.length;
int left = 0, right = m;
int median1 = 0, median2 = 0;
while (left <= right) {
int i = (left + right) / 2;
int j = (m + n + 1) / 2 - i;
int nums_im1 = (i == 0 ? Integer.MIN_VALUE : nums1[i - 1]);
int nums_i = (i == m ? Integer.MAX_VALUE : nums1[i]);
int nums_jm1 = (j == 0 ? Integer.MIN_VALUE : nums2[j - 1]);
int nums_j = (j == n ? Integer.MAX_VALUE : nums2[j]);
if (nums_im1 <= nums_j) {
median1 = Math.max(nums_im1, nums_jm1);
median2 = Math.min(nums_i, nums_j);
left = i + 1;
}
else {
right = i - 1;
}
}
return (m + n) % 2 == 0 ? (median1 + median2) / 2.0 : median1;
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
| class Solution(object):
def findMedianSortedArrays1(self, nums1, nums2):
"""
:type nums1: List[int]
:type nums2: List[int]
:rtype: float
"""
m = len(nums1)
n = len(nums2)
lens = m+n
left, right = -1, -1
aStart,bStart = 0,0
for i in range(lens//2+1):
left = right
if aStart<m and (bStart >= n or nums1[aStart] < nums2[bStart]):
right = nums1[aStart]
aStart+=1
else:
right = nums2[bStart]
bStart+=1
if (lens & 1) == 0:
return (left+right)/2.0
else:
return right
def findMedianSortedArrays(self, nums1, nums2):
def getKthElemnt(k):
index1, index2 = 0, 0
while True:
if index1 == m:
return nums2[index2+k-1]
if index2 == n:
return nums1[index1+k-1]
if k==1:
return min(nums1[index1], nums2[index2])
newIndex1 = min(index1 + k//2 -1, m-1)
newIndex2 = min(index2 + k//2 -1, n-1)
privot1,privot2 =nums1[newIndex1], nums2[newIndex2]
if privot1<=privot2:
k-=newIndex2-index1 +1
index1 = newIndex2 + 1
else:
k -= newIndex2 - index2 +1
index2 = newIndex2 +1
m,n = len(nums1), len(nums2)
totalLength = m+n
if totalLength % 2==1:
return getKthElemnt((totalLength+1)//2)
else:
return (getKthElemnt(totalLength//2)+ getKthElemnt(totalLength//2+1)) /2
def findMedianSortedArrays(self, nums1: List[int], nums2: List[int]) -> float:
if len(nums1) > len(nums2):
return self.findMedianSortedArrays(nums2, nums1)
infinty = 2**40
m, n = len(nums1), len(nums2)
left, right = 0, m
median1, median2 = 0, 0
while left <= right:
i = (left + right) // 2
j = (m + n + 1) // 2 - i
nums_im1 = (-infinty if i == 0 else nums1[i - 1])
nums_i = (infinty if i == m else nums1[i])
nums_jm1 = (-infinty if j == 0 else nums2[j - 1])
nums_j = (infinty if j == n else nums2[j])
if nums_im1 <= nums_j:
median1, median2 = max(nums_im1, nums_jm1), min(nums_i, nums_j)
left = i + 1
else:
right = i - 1
return (median1 + median2) / 2 if (m + n) % 2 == 0 else median1
|