1-两数之和到四数之和

给定一个整数数组 nums 和一个整数目标值 target，请你在该数组中找出 和为目标值 target 的那 两个 整数，并返回它们的数组下标。

你可以假设每种输入只会对应一个答案。但是，数组中同一个元素在答案里不能重复出现。

你可以按任意顺序返回答案。

示例 1：

输入：nums = [2,7,11,15], target = 9
输出：[0,1]
解释：因为 nums[0] + nums[1] == 9 ，返回 [0, 1] 。
示例 2：

输入：nums = [3,2,4], target = 6
输出：[1,2]
示例 3：

输入：nums = [3,3], target = 6
输出：[0,1]

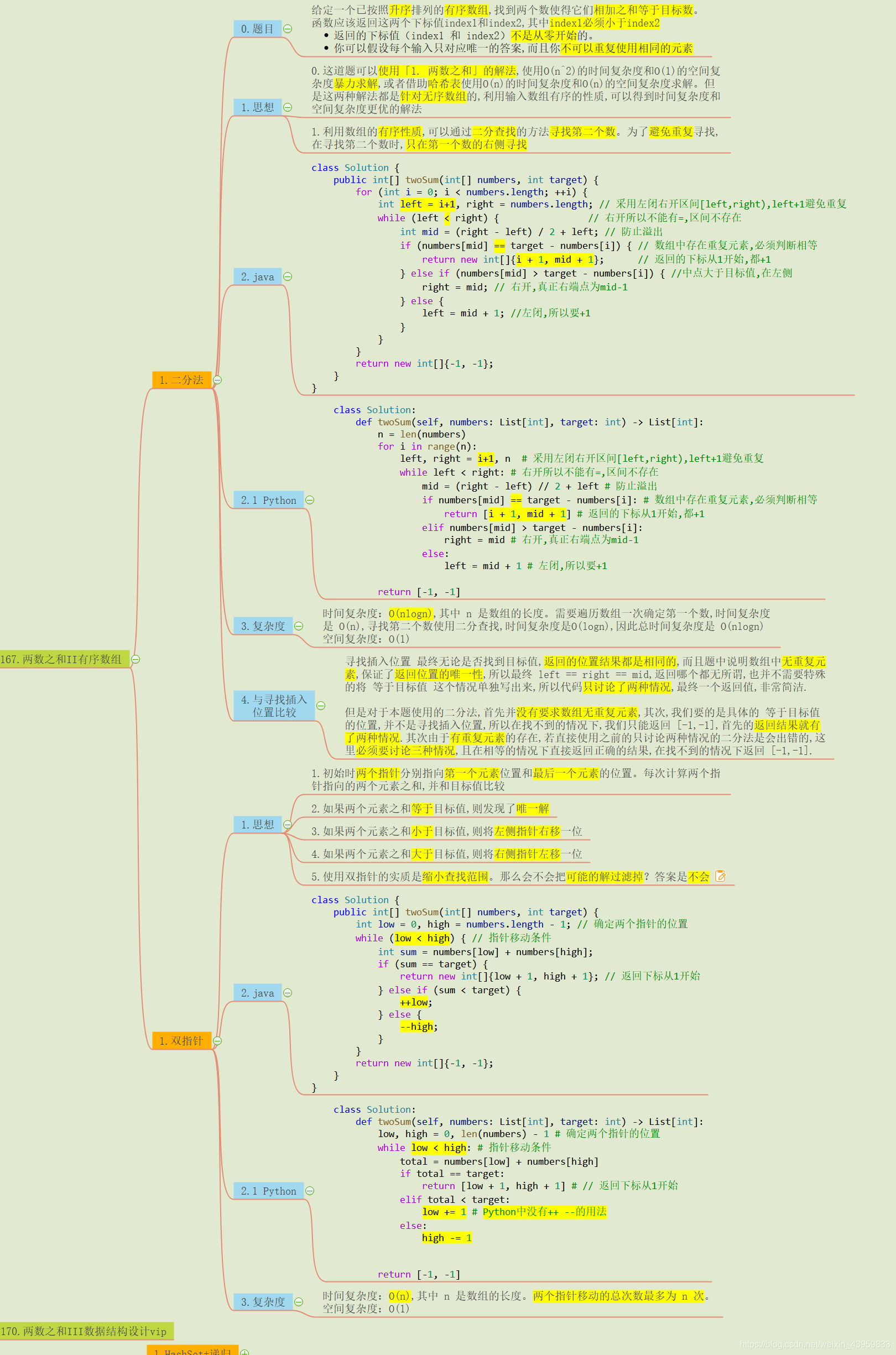
两数之和

哈希表法

哈希表的方法首先用在了两数之和(无序数组)上, 哈希表的使用最主要的目的就是为了降低时间复杂度, 缩减寻找第二个元素使用的时间(将时间复杂度由O(n)降为O(1)), 其中无序数组是哈希表使用的重要条件, 因为当数组有序后, 我们完全可以直接使用 双指针 的方法来降低时间复杂度, 它的使用比 哈希表 更加方便快捷, 空间复杂度也更低, 所以数组有序之后, 我们应该首选 双指针 的方法.

在使用哈希表的时候, 也有一个很重要的优化点, 就是 遍历两遍哈希表 和 遍历一遍哈希表 的区别. 简单来说就是, 如果我们先将第一个元素放入哈希表中, 然后再寻找第二个元素, 那么我们就需要 遍历两遍哈希表, 如果我们先寻找第二个元素, 之后再将元素放入到哈希表中, 那么就只需要 遍历一遍哈希表.

上面是我们第一次使用哈希表的情况, 第二次使用哈希表就到了 《四数之和II四数组相加》, 首先由于它具有四个独立的数组, 相当于四维空间, 所以我们很难在这么高的空间维度上直接使用 双指针 的方法, 其次它并没有要求 不重复元组 的情况, 这就给了我们使用 哈希表 的可能性, 因为不用担心复杂的去重操作, 但是使用哈希表一般也是两维的空间, 所以我们必须先进行降维操作, 也就是将四个数组进行分组, 由三种结果的时间复杂度来判断, 我们很容易就选择了 两两分组 的情况.

之后对于哈希表的使用, 就是两种不同情况的使用了。如果需要直接返回相应数组的下标值, 那是很简单的, 我们只需要将 下标值 当做 哈希表的值 即可。(两数之和中的使用)

1
2
3
4
5
6
7
8
9
10
public int[] twoSum(int[] nums, int target){
  	Map<Integer,Integer> map = HashMap<Integer,Integer>();
  	for(int i=0;i < nums.length;i++){
      	if(map.containsKey(target - nums[i])){
          	return new int[]{map.get(target-nums[i]), i};
        }
      	map.put(nums[i], i);
    }
  	return new int[0];
}
1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution(object):
    def twoSum(self, nums, target):
        """
        :type nums: List[int]
        :type target: int
        :rtype: List[int]
        """
        hashtable = dict()
        for i,num in enumerate(nums):
          	if target - num in hashtable:
              	return [hashtable[target-nums], i]
            hashtable[num] = i
        return []

双指针法

对于n数之和, 除了哈希表的方法, 最常用的就是 双指针 的方法了, 上文也提到了, 使用双指针最重要的条件就是数组是有序的, 当然这只是针对n数之和的题型, 对于其他题型, 并不需要要求数组是有序

在n数之和中使用双指针必要条件就是数组是有序的, 这就需要我们根据实际情况来判断 数组是否需要进行排序. 比如在 两数之和 中, 就算使用暴力法也才$O(n^2)$, 但进行排序最快也需要$O(nlogn)$的时间复杂度, 所以对于两数之和来说, 是真的没必要.

但是对于 三数之和 和 四数之和 就很有必要了, 因为它们时间复杂度实在太高了, 最关键的是它们元组的重复情况也比较多, 想利用哈希表进行去重是非常困难的, 最终只能选择将数组排序后使用 双指针 的方法.

167. 两数之和 II - 输入有序数组

两数之和中有序和无序的区别

在无序数组中寻找第二个数就没有多少捷径, 毕竟数组无序, 很多经典的方法都用不上, 最后只能牺牲空间来换取时间, 利用哈希表将空间复杂度增加到了$O(n)$, 从而降低了寻找第二个数的时间复杂度.

但是当数组有序之后, 就能使用一些经典的算法同时仍然保证空间复杂度为O(1), 不需要牺牲空间来换取时间, 比如下面马上介绍的 二分法 和 双指针 方法.

这里给我们提供了一种思维, 那我们是不是也可以将无序数组先进行排序后, 再使用这些经典算法呢? 当然可以这么做, 但对于两数之和来说, 必要性不是太大. 因为最快的排序算法也需要O(nlogn)的时间复杂度, 对于两数之和确实提升也不是太大, 但是对于 三数之和/四数之和 还是挺实用的,

二分法和寻找插入位置的区别

数组有序了，使用二分法寻找第二个数可以将时间复杂度降到$O(nlogn)$ 。

寻找插入位置无论，最终无论是否找到目标值，返回的位置结果都是相同的，而且题中说明数组中无重元素，保证了返回位置的唯一性，所以最终 left == right == mid，返回哪个都无所谓，也并不是需要特殊的将等于目标值这种情况单独写出来。所以代码只讨论了两种情况，最终返回一个值，非常简洁。

本题使用的二分法，首先并没有要求数组无重复元素，其次我们要的是具体的等于目标值的位置，并不是寻找插入位置，所以在找不到的情况下，只能返回[-1,-1]。首先的返回结果就有了两种情况.

其次由于有重复元素的存在, 若直接使用之前的只讨论两种情况的二分法是会出错的, 这里必须要讨论三种情况, 且在相等的情况下直接返回正确的结果, 在找不到的情况下返回 [-1, -1].

本题另外的一个小的注意点是: 返回的下标从1开始, 只要在原本的返回结果上+1就可以了.

还有一个注意点是, 为了避免重复寻找,在寻找第二个数时,只在第一个数的右侧寻找, 也就是left = i+1.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
class Solution(object):
    # 二分法
    def twoSum(self, numbers, target):
        """
        :type numbers: List[int]
        :type target: int
        :rtype: List[int]
        """
        n = len(numbers)
        for i in range(n):
            left, right = i+1, n  # 采用左闭右开区间[left, right), left+1避免重复
            while left<right:
                mid = (right - left) //2 + left; # 防止溢出
                if numbers[mid] == target - numbers[i]: # 数组中存在重复元素，必须判断相等
                    return [i+1, mid+1]
                elif numbers[mid] > target - numbers[i]:
                    right = mid # 右开，真正右端点为mid-1
                else:
                    left = mid + 1 # 左闭，所以小+1
        return [-1, -1]
    # 双指针
    def twoSum1(self, numbers, target):
        low, high =0, len(numbers-1)
        while low<high:
            total = numbers[low] + numbers[high]
            if total == target:
                return [low+1, high+1] # 返回下标从1开始
            elif total<target:
                low+=1
            else:
                high-=1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
class Solution {
    // 二分法
    public int[] twoSum(int[] numbers, int target) {
        for(int i=0;i<numbers.length;i++){
            int left = i+1, rigth = numbers.length;  // 采用左闭右开区间[left,right),left+1避免重复
            while(left<right){
                mid = left + right /2 + left; // 防止溢出
                if(numbers[mid] == target - numbers[i]){ // 数组中存在重复元素,必须判断相等
                    return new int[]{i+1, mid+1} ; // 返回的下标从1开始,都+1
                }else if(numbers[mid] > target-numbers[i]){ //中点大于目标值,在左侧
                    right = mid;//右开，真正右端点为mid-1
                }else{
                    left = mid+1; // 左闭 +1
                }
            }
        }
        return new int[]{-1,-1};
    }
    // 双指针法
    public int[] twoSum2(int[] numbers, int target){
        int low = 0, high = numbers.length-1;
        while (low < high) { // 指针移动条件
            int sum = numbers[low] + numbers[high];
            if (sum == target) {
                return new int[]{low + 1, high + 1}; // 返回下标从1开始
            } else if (sum < target) {
                ++low;
            } else {
                --high;
            }
        }
        return new int[]{-1, -1};
    }
}

三数之和

15. 三数之和

难点在于题目要求的不重复的三元组，它的可重复情况是非常多的，无法像两数之和那样，只要将第一个元素放入哈希表中，就可以轻松解决元素重复的问题了。

对于三数之和，即使使用哈希表去重，它的操作也是比较困难的，所以不能简单的使用三重循环枚举所有的三元组，然后用哈希表去重，这样工作量比较大。

因此必须换一种做法，从源头上解决元素重复问题，如果给定数组是有序的，那么其中可重复的情况就是可控的了，处理起来也简单，所以先把数组从小到大排序，随后用普通的三重循环就可。

然后就会发现，重复的元素都是相邻元素，只要保证每一重循环时，相邻两次枚举的元素不是相同的元素，这样就可以避免元组重复的情况了。

双指针

使用普通的三层循环确实也能解决问题, 但是 $O(n^3)$ 的时间复杂度也确实太高了, 这时我们想到了在 有序数组的两数之和 中使用的双指针的方式, 虽然现在是三数之和, 但当我们正常遍历了第一层循环之后, 剩下的两个数不就形成了 有序数组的两数之和 了吗? 所以我们只要 保持第二重循环不变, 而将第三重循环变成一个从数组最右端开始向左移动的指针, 同时加上上述讨论的避免重复的条件, 最终代码就完成了.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
class Solution {
    public List<List<Integer>> threeSum(int[] nums) {
        List<List<Integer>> res = new ArrayList<>();
        if(nums.length==0 ||  (nums[0]==0 && nums.length==1))  return res;

        Arrays.sort(nums);

       
        // 枚举a
        for(int first=0;first<nums.length;first++){
            //需要和上一次枚举的数不同
            if(first>0 && nums[first] == nums[first-1]){
                continue;
            }
            // c对应的指针初始指向数组的最右排
            int third = nums.length-1;
            int target = -nums[first];
            //枚举b
            for(int second= first+1 ;second<nums.length;second++){
                // 需要和上一次枚举不同
                if(second > first+1 && nums[second] == nums[second-1]) {
                    continue;
                }
                // 需要保证b指针在c指针的左侧
                while(second < third && nums[second]+nums[third] > target){
                    --third;
                }
                //如果指针重合，后续也不会满足条件，可以退出循环
                if(second==third) break;
                if (nums[second] + nums[third] == target){
                    res.add(Arrays.asList(nums[first],nums[second],nums[third]));
                }
            }

        }
        return res;

    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution(object):
    def threeSum(self, nums):
        """
        :type nums: List[int]
        :rtype: List[List[int]]
        """
        res = list()
        if len(nums) == 0: return res
        nums.sort()

        # 枚举a
        for first in range(len(nums)):
            if first>0 and nums[first] == nums[first-1]:
                continue
            thrid = len(nums) -1
            target = -nums[first]
            for second in range(first+1, len(nums)):
                if second> first+1 and nums[second] == nums[second-1]:
                    continue
                while second<thrid and nums[second] + nums[thrid] > target:
                    thrid-=1
                if second==thrid:
                    break
                if nums[second]+nums[thrid] == target:
                    res.append([nums[first], nums[second], nums[thrid]])
        return res

三数之和变体

16. 最接近的三数之和

还是使用双指针解决

排序+双指针

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
class Solution {
    public int threeSumClosest(int[] nums, int target) {
        Arrays.sort(nums);
        int n = nums.length;
        int best = 10000000;

        // 枚举 a
        for (int i = 0; i < n; ++i) {
            // 保证和上一次枚举的元素不相等
            if (i > 0 && nums[i] == nums[i - 1]) {
                continue;
            }
            // 使用双指针枚举 b 和 c
            int j = i + 1, k = n - 1;
            while (j < k) {
                int sum = nums[i] + nums[j] + nums[k];
                // 如果和为 target 直接返回答案
                if (sum == target) {
                    return target;
                }
                // 根据差值的绝对值来更新答案
                if (Math.abs(sum - target) < Math.abs(best - target)) {
                    best = sum;
                }
                if (sum > target) {
                    // 如果和大于 target，移动 c 对应的指针
                    int k0 = k - 1;
                    // 移动到下一个不相等的元素
                    while (j < k0 && nums[k0] == nums[k]) {
                        --k0;
                    }
                    k = k0;
                } else {
                    // 如果和小于 target，移动 b 对应的指针
                    int j0 = j + 1;
                    // 移动到下一个不相等的元素
                    while (j0 < k && nums[j0] == nums[j]) {
                        ++j0;
                    }
                    j = j0;
                }
            }
        }
        return best;
    }
}

时间复杂度：$O(N^2)$ 其中 N 是数组 $\textit{nums}$ 的长度。我们首先需要 $O(N \log N)$ 的时间对数组进行排序，随后在枚举的过程中，使用一重循环 O(N) 枚举 a，双指针 O(N) 枚举 b 和 c，故一共是 O(N^2)

空间复杂度：$O(\log N)$。排序需要使用 $O(\log N)$ 的空间。然而我们修改了输入的数组 $\textit{nums}$，在实际情况下不一定允许，因此也可以看成使用了一个额外的数组存储了 $\textit{nums}$ 的副本并进行排序，此时空间复杂度为 O(N)。

四数之和

18. 四数之和

思想同三数之和：排序+双指针

四数之和 本质上 和三数之和一样的，由于都有大量的重复元素在，都不能使用哈希表进行简单的去重，都需要先进行排序后才方便遍历处理，同时为了优化时间复杂度，再加上双指针方法的使用，如果只是想简单实现的话，那么在三数之和上直接多加一重循环。但在代码上不同点在于：并非只是简单的家一重循环而已，而是进行了优化处理。

因为四数之和相比较于三数之和来说，情况更加复杂，时间复杂度也比较高，而且这个时间复杂度通过算法降下来很难。只能通过对代码的优化，直接减少大量不必要的遍历情况，从而来缩短代码的运行时间。

对于代码的优化主要分为两大块：一部分是为了避免出现重复的四元组，在遍历上的优化，这部分和三数之和相似，不过更复杂。

首先是对前两重循环进行的去重操作, 当 i 或者 j 的值与前面的值相等时忽略, 之后又对 双指针 进行了去重操作, 这里有个重要的注意点: 一定注意代码中是 先进行了指针的移动还是先进行了去重的比较, 对于不同的顺序, 比较的元素是完全不同的. 如果先进行了指针的移动, 对于左指针来说, 需要比较的元素就是 当前元素和前面的一个元素, 如果是先进行去重的比较, 那比较的元素就是 当前元素和后面的一个元素, 再进行指针的移动. 对于右指针的情况正好是完全相反的.

第二部分就是在循环遍历中先通过计算特定的四个数之和, 以此来判断接下来的循环操作情况.

比如 在确定第一个数 nums[i] 之后, 如果nums[i]+nums[i+1]+nums[i+2]+nums[i+3]>target, 也就是此时的最小的4个数之和都大于target, 说明此时剩下的三个数无论取什么值, 四数之和一定大于 target, 因此直接退出第一重循环就可以了

在确定第一个数 nums[i] 之后,如果nums[i]+nums[n−3]+nums[n−2]+nums[n−1]<target, 也就是此时的最大的4个数之和都小于target, 说明此时剩下的三个数无论取什么值, 四数之和一定小于 target,因此第一重循环直接进入下一轮, 枚举nums[i+1], 使用 continue 关键字.

对于第二层循环也是同样的判断方法, 通过这两层循环的判断优化, 能直接删去大量的不满足情况, 减少代码运行的时间. 这也能给我们带来启发, 在算法层面不能进行优化的时候, 可以选择对代码的细节进行优化, 同样可以起到节省时间的效果.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
class Solution(object):
    def fourSum(self, nums, target):
        """
        :type nums: List[int]
        :type target: int
        :rtype: List[List[int]]
        """
        res = list()
        length = len(nums)
        if not nums or length<4:
            return res

        nums.sort()
        # 定义4个指针i,j,left,right  i从0开始遍历,j从i+1开始遍历,留下left和right作为双指针
        for i in range(length - 3):
            if i > 0 and nums[i] == nums[i - 1]: # 当i的值与前面的值相等时忽略
                continue
            # 获取当前最小值,如果最小值比目标值大,说明后面越来越大的值根本没戏
            if nums[i] + nums[i + 1] + nums[i + 2] + nums[i + 3] > target:
                break # 这里使用的break,直接退出此次循环,因为后面的数只会更大
            # 获取当前最大值,如果最大值比目标值小,说明后面越来越小的值根本没戏,忽略
            if nums[i] + nums[length - 3] + nums[length - 2] + nums[length - 1] < target:
                continue # 这里使用continue,继续下一次循环,因为下一次循环有更大的数
            # 第二层循环j,初始值指向i+1
            for j in range(i + 1, length - 2):
                if j > i + 1 and nums[j] == nums[j - 1]: # 当j的值与前面的值相等时忽略
                    continue
                if nums[i] + nums[j] + nums[j + 1] + nums[j + 2] > target:
                    break
                if nums[i] + nums[j] + nums[length - 2] + nums[length - 1] < target:
                    continue
                left, right = j + 1, length - 1
                # 双指针遍历,如果等于目标值,left++并去重,right--并去重,当当前和大于目标值时right--,当当前和小于目标值时left++
                while left < right:
                    total = nums[i] + nums[j] + nums[left] + nums[right]
                    if total == target:
                        res.append([nums[i], nums[j], nums[left], nums[right]])
                        left += 1 # left先+1之后,和它前面的left-1进行比较,若后+1,则和它后面的left+1进行比较
                        while left < right and nums[left] == nums[left - 1]:
                            left += 1
                        right -= 1
                        while left < right and nums[right] == nums[right + 1]:
                            right -= 1   
                    elif total < target:
                        left += 1
                    else:
                        right -= 1
        return res
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
class Solution {
    public List<List<Integer>> fourSum(int[] nums, int target) {
        List<List<Integer>> res = new ArrayList<>();
        if(nums==null || nums.length==0) return res;
        int length=nums.length;

        Arrays.sort(nums);

        // 定义4个指针， i,j,left,right  i从0开始遍历，j从i+1开始遍历，留下left和right作为双指针
        for(int i=0;i<length - 3;i++){
            if(i > 0 && nums[i] == nums[i-1]) continue;

            // 获取当前最小值，如果最小值比目标值大，说明后面越来越大的值根本没戏
            if(nums[i] + nums[i+1] + nums[i+2] +nums[i+3] > target){
                break; // 这里使用的break，直接退出此次循环，因为后面的数只会更大
            }

            // 获取当前最大值，如果最大值比目标值小，说明后面的值越来越小
            if(nums[i] + nums[length-3] + nums[length-2] + nums[length-1] < target){
                continue; // 继续下一次循环，因为下一次循环有更大的数
            } 

            // 第二层循环j，初始值指向i+1
            for(int j=i+1; j<length-2;j++){
                if(j>i+1 && nums[j] == nums[j-1]){  // 当j的值与前面的值相等时忽略
                    continue;
                }

                if(nums[i] + nums[j] + nums[j+1] + nums[j+1] > target) {
                    break;
                }

                if(nums[i] + nums[j] + nums[length-2] + nums[length-1] < target){
                    continue;
                }

                int left = j+1, right=length-1;
                //双指针遍历，如果等于目标值，left++并去重，right--并去重，当当前和大于目标值时right-- 否则left++
                while(left < right){
                    int sum = nums[i] + nums[j] + nums[left] + nums[right];
                    if(sum==target){
                        res.add(Arrays.asList(nums[i], nums[j], nums[left], nums[right]));
                        left++; // left先+1之后，和它前面的left-1进行比较，若后+1，则和它后面的left+1进行比较
                        while(left < right && nums[left]==nums[left-1]){
                            left++;
                        }
                        right--;
                        while(left<right && nums[right]== nums[right+1]){
                            right--;
                        }
                    }else if(sum<target){
                        left++;
                    }else{
                        right--;
                    }

                }

            }
            
        }
        return res;
    }
}

四数之和二

454. 四数相加 II

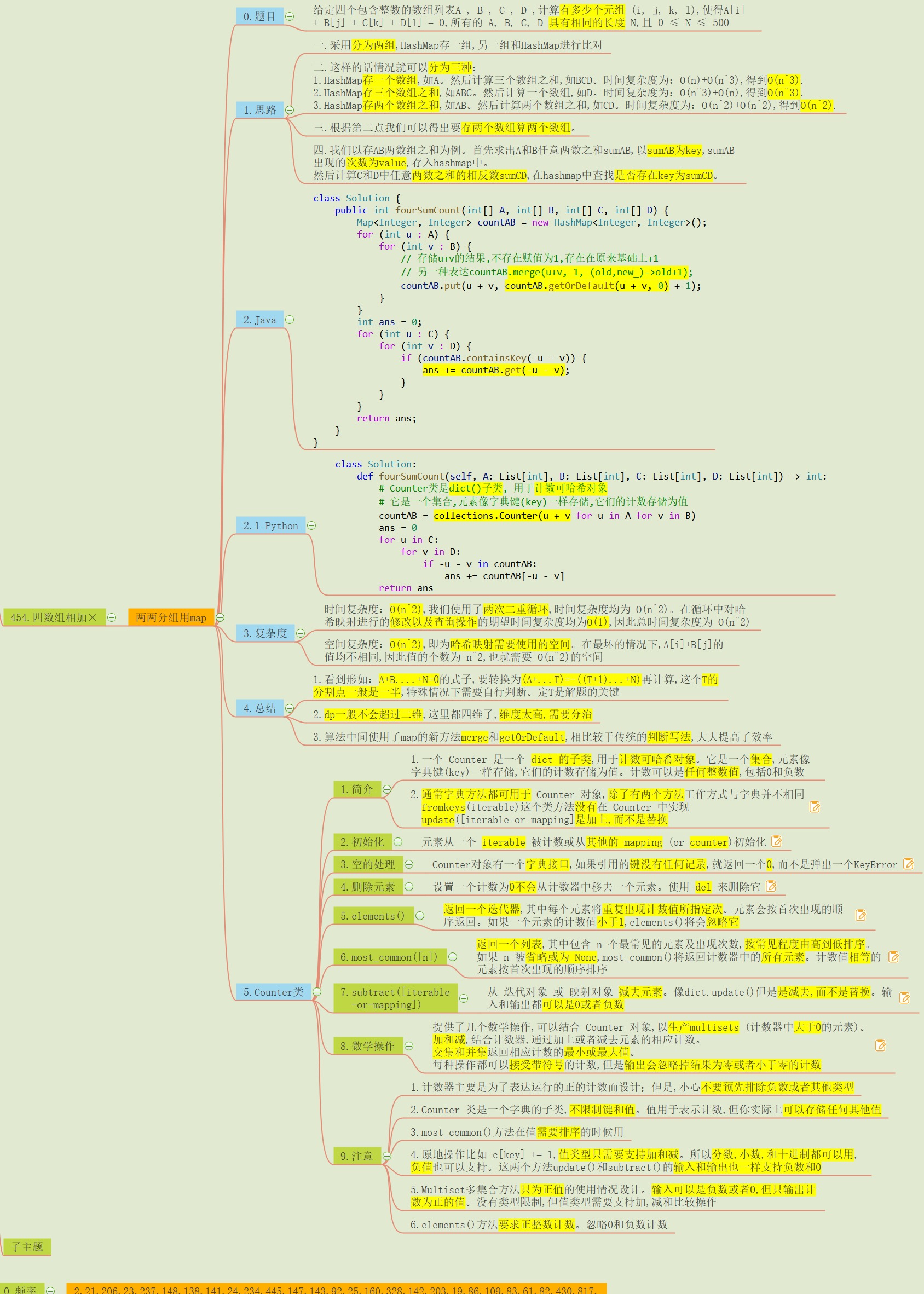
维数太高，分治处理

此题一看似乎和四数之和差不多，但本质上却有很大的区别，首先无论是三数之和还是四数之和，它们都是在一个数组上的操作，本质上都是一维的，同时它们都要求找到不重复的元组，这就限制了我们不能简单的使用哈希表进行去重操作。最终只能将数组排序后使用双指针。

但本题是四个独立的数组，相当于是四个维度，想在四个维度上使用双指针的方法显然不现实。同时此题只要求我们找到所有4个元素的和为0的元组个数即可，并没有要求是不重复的元组，这样就简单了很多，也是可以使用哈希表法。

此题是在使用哈希表的时候，会遇到如下三种情况：

  • hashmap存一个数组，如A。然后计算三个数组之和，如BCD。时间复杂度为：$O(n)+O(n^3)=O(n^3)$
  • hashmap存三个数组之和，如ABC。然后计算一个数组，如D。时间复杂度为：$O(n^3)+O(n) = O(n^3)$
  • hashmap存两个数组之和，如AB，然后计算两个数组之和，如CD，时间复杂度为：$O(n^2)+O(n^2) = O(n^2)$

根据事件复杂度来看，选第三种情况

确定了使用的方法(哈希表)以及分类方法(两两分组)。此题和两数之和中使用的哈希表有很大的区别，在两数之和中，我们需要的是满足条件的下标值，所以在哈希表中存的是元组的下标值。

但在本题中，我们需要的是元组个数，所以哈希表中的值应存取出现的次数，这就有点难度。使用java map中的merge或getOrDefault

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
    public int fourSumCount(int[] A, int[] B, int[] C, int[] D) {
        int res = 0;
        if(A.length==0) return res;

        Map<Integer,Integer> countAB = new HashMap<>();
        for(int u: A){
            for(int v:B){
                // 存储u+v的结果，不存在赋值为1，存在在原来基础上+1
                // 另一种表达countAB.merge(u+v, 1, (old,new_)-> old+1);
                countAB.put(u+v, countAB.getOrDefault(u+v, 0) + 1);
            }
        }

        for(int u: C){
            for(int v:D){
                if(countAB.containsKey(-u-v)){
                    res+=countAB.get(-u-v);
                }
            }
        }
        return res;

    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution(object):
    def fourSumCount(self, A, B, C, D):
        """
        :type nums1: List[int]
        :type nums2: List[int]
        :type nums3: List[int]
        :type nums4: List[int]
        :rtype: int
        """
        # Counter类是dict()子类，用于计数可哈希对象
        # 它是一个集合，元素字段键(key) 一样存储，他们的技术存储为值
        countAB = collections.Counter(u+v for u in A for v in B)
        ans = 0 
        for u in C:
            for v in D:
                if -u-v in countAB:
                    ans+=countAB[-u-v]
        return ans

n数之和方法总结

对于两数之和，看它是否有序的，如果是无序的就用哈希表法，如果是有序的可以使用双指针。

对于一个数组上的三数之和、四数之和等，无论数组是否有序，都排序后使用双指针法

对于多个数组之和的情况，首先对它们进行分组来实现降维操作，一般来说分为两个相等的小组，之后再使用哈希表法。