Breadth First Reasoning Graph for Multi-hop Question Answering

为了解决GNNs不必要的更新和简单的边结构阻碍直接提取准确的答案跨度，和更可解释性。

作者提出了一种新的广度优先推理图(BFR-Graph)模型，它提供了一种新的更符合推理过程的消息传递方式。

在BFR-Graph中，推理信息要求从问题结点开始，逐跳传递到下一个句子结点，直到所有的边都经过，可以有效地防止每个结点的过度平滑或不必要的多次更新。

为了引入更多的语义，我们还将推理图定义为考虑了共现关系数和句子间距离的加权图。

然后基于GNN提出了一种更直接、更易解释的方法来聚合不同粒度级别的分数。

现有GNN方法的几个问题

  • 首先，当前的方法将所有节点（包括一些不必要的节点）一起更新到每一层中，这可能导致节点收敛到相似的值，并失去对具有更多层的GNN的识别能力。
  • 第二，虽然GNN设计了不同类型的边，但是在没有考虑句子之间的其他关系信息的情况下，相同类型的边之间没有更细粒度的区别。
  • 第三，现有的方法只是潜在地融合了GNN和上下文编码器的隐藏表示，而没有以直接和可解释的方式进行答案广度提取。

方法

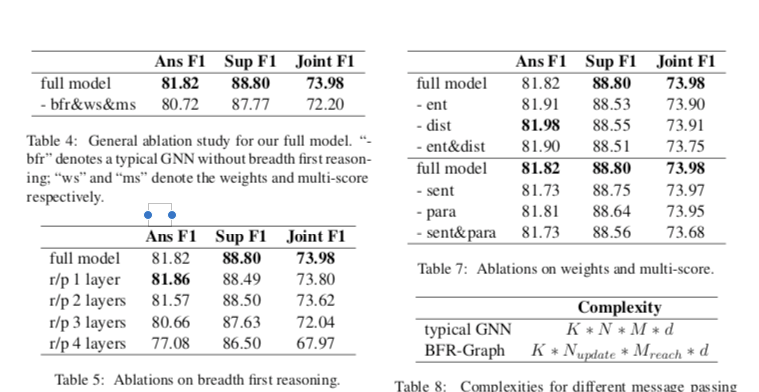
与现有的基于GNN的方法不同，BFR-Graph对消息传递引入了新的限制：消息只从问题开始，然后逐跳传递到后面的句子节点。此外，考虑到共现实体和句子之间的距离，图被构造成一个加权图。此外，利用BFR图的推理结果，设计了多分数答案预测。

简言之，我们在加权图上提出了广度优先推理，然后在多任务联合训练的框架下，结合多级分数进行回答预测。

Paragraph Selection

训练一个二分类bert，对每个段落进行打分，选择得分在前N位的段落作为有用的段落，然后将这些段落连接在一起作为上下文C。

Context Encoding

bert输出+bi-attention后获得问题和上下文的编码表达

其中L是输入序列的长度(连接问题和上下文)，d是双关注层的输出维度(也是BERT的维度)。

为了实现句子级表示，首先获得每个句子的标记级表示：

获得每个句子的表示是用了Bi-LSTM的方法

$\alpha_k^i$ 是第i个句子中第k个token的权重，通过两层MLP output size=1获得

Weighted Graph Construction

为了更好地挖掘句子之间复杂的关系信息，定义了正相关和负相关两种类型的相关性：

  • 正相关：如果表示句子 $i$ 和 $j$ 的节点具有 n(n≥1) 个相同命名实体，则添加一条边，该边的权重为：
  • 负相关：否则，如果两个节点最初来自同一段落，则添加一条边，该边的权重为：

其中d是两个句子的距离(例如，如果该句子紧跟在段落中的另一个句子之后，则d=1，如果它们之间有句子，则d=2，依此类推)。K1和K2是超参数。

是同质图，它包含单一类型的节点和边。

Breadth First Reasoning

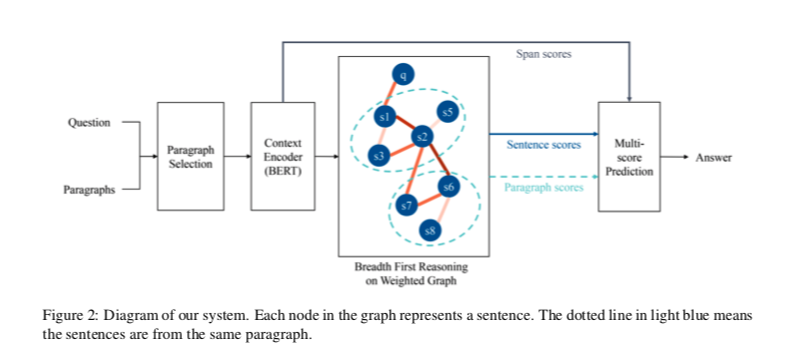
下图直观地显示了BFR-Graph和典型GNN之间的区别。

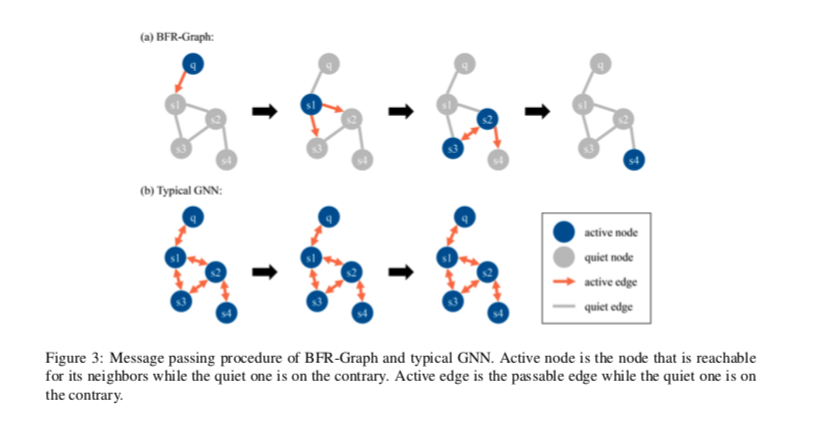
当我们在段落上推理来回答一个问题时，我们从问题开始，一跳一跳地找到下一个句子。

对于节点表示句子的GNN，以下消息传递是不必要的，可能会抑制无用节点的干扰：

  • 从后一个节点到前一个节点
  • 某个节点尚未收到来自问题的消息，但它会更新其他节点。

具体地说，当同时满足以下条件时，节点i由节点j更新：

  • 节点 $i$ 和节点 $j$ 是邻居
  • 节点 $j$ 是Active的
  • 节点 $i$ 和节点 $j$ 之间的边以前没有经过

BFR-Graph的整个消息传递过程:

消息更新传递的函数还是GAT

Multi-score Answer Prediction

HotpotQA数据集中的答案是上下文的span。现有工作仅计算编码器输出（如BERT）上的跨度概率，或额外连接GNN的隐藏输出。不同的是，我们通过计算从GNN获得的句子分数和段落分数来使用更易于解释的方法。如下图：

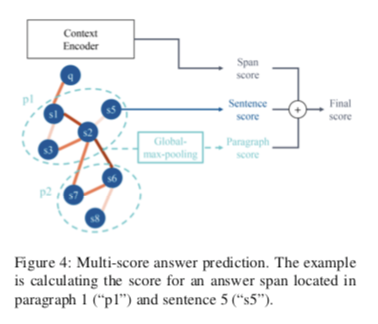
通常，作为答案跨度的开始/结束的上下文中的第y个单词的分数通过以下方式计算：

然后，计算GNN中每个节点对应的句子得分：

计算段落分数, 通过全局最大池：

$s_i^{P_j}$是第$i$句话在第Pj段中的表达。这也可以通过在所有语句节点上取每个维度上的最大隐藏值来实现。

最后，上下文中第y个单词作为答案范围开始的概率由以下公式确定：

并且可以类似地计算上下文中的第y个单词作为答案跨度结束的概率。

如果一个句子或段落的得分较高，则位于其中的单词更有可能是答案。

最后是一个多任务预测

消融实验