Do Transformers Really Perform Bad for Graph Representation?
Do Transformers Really Perform Bad for Graph Representation?
作者提出了一个建立在Transformer体系结构上可以对图进行出色表征的模型——Graphormer。
近来Transformer和Graph进行结合尝试的文章有:
- Graph transformer for graph-to-sequence learning. AAAI 2020.
- A generalization of transformer networks to graphs. AAAI 2021. (GT)
- Heterogeneous graph transformer. 2020.
- Re-thinking graph transformers with spectral attention. 2021. (>GT)
- Graph transformer. 2019.
- Direct multi-hop attention based graph neural network. 2020
- Graph transformer networks. 2019.
- Transformers are Graph Neaurl Networks. 2020
- Graph-bert: Only attention is needed for learning graph representations. 2020
虽然有很多利用Transformer进入图形领域的尝试,但唯一有效的方法是用Softmax attention 取代经典GNN变体中的一些关键模块(例如,特征聚合)。因此,Transformer体系结构是否适合于对图进行建模,以及如何使其在图表示学习中发挥作用,仍然是一个悬而未决的问题。
本文方法
How Transformers could perform well for graph representation learning?
作者解决办法:关键是要正确地将图的结构信息融入到模型中。
Centrality Encoding:捕捉节点在图中的重要性。在图中,不同的节点可以具有不同的重要性,例如,名人被认为比社交网络中的大多数网络用户更有影响力。然而,这种信息没有反映在self-attention模块中,因为它主要使用节点语义特征来计算相似度。
1.1. degree centrality :利用度中心性进行Centrality Encoding,其中根据每个节点的度将可学习向量分配给每个节点,并将其添加到输入层中的节点特征。
Spatial Encoding :提出了一种新的空间编码来捕捉节点之间的结构关系。将图形结构化数据与其他结构化数据(例如语言、图像)区分开来的一个值得注意的几何属性是不存在用于嵌入图形的规范网格,结点只能位于非欧几里德空间中,并且由边连接。作者使用任意两个节点之间的最短路径距离作为示例,将其编码为Softmax关注度中的偏置项,以帮助模型准确地捕捉图中的空间相关性。
2.1. 此外,有时edge特征中还包含额外的空间信息,例如分子图中两个原子之间的键类型。设计了一种新的Edge Encoding方法,将这种信号进一步带入Transformer layers。
Graphormer
Structural Encodings in Graphormer
三种有效的Graphormer编码:Centrality Encoding、Spatial Encoding、Edge Encoding in the Attention
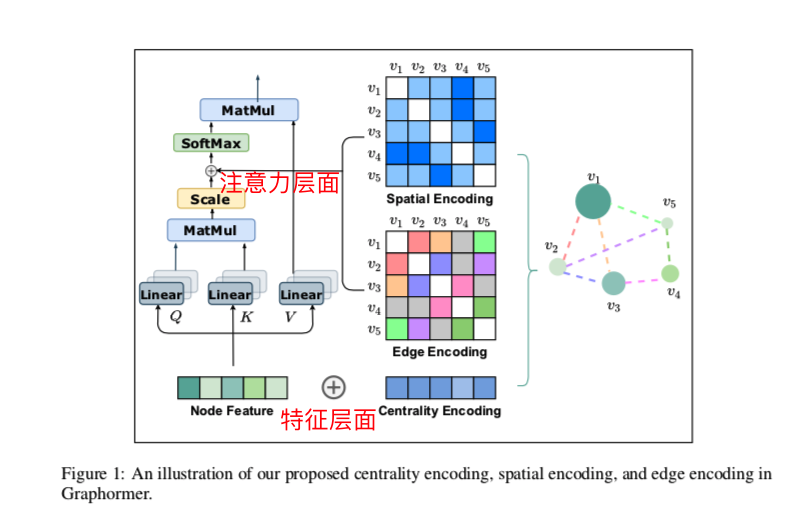
特征层面 Centrality Encoding
普通的attention机制是基于节点之间的语义相关性来计算注意力分布的,节点的中心性可以衡量节点在图中的重要性,但这种信息在目前的attention计算中被忽略了。(attention不是也可以计算出什么比较重要吗,这里有点疑问)
在Graphormer中,作者使用了degree中心性,作为节点中心性的度量。根据每个节点的入度和出度为每个节点分配两个实值embedding向量。对每个节点都应用中心性编码,因此需将其作为输入添加到节点特征中。
通过在输入中使用中心性编码,Softmax注意力既可以捕捉到查询和关键字中的节点重要性信号,又能捕捉到节点的重要性。
1 | self.in_degree_encoder = nn.Embedding(512, hidden_dim, padding_idx=0) |
注意力层面 Spatial Encoding
original的transformer的注意力机制使得它具有全局的感受野,前提是对于每一个token需要指定一个位置,比如一个句子中不同词的位置可以用 $1,2,3,4……$ 来代表序列中不同位置的编码。对于图来说并不存在序列这样的位置特性,那么应该如何考虑不同节点的位置信息呢?
图结构通常是在非欧空间下的,两个节点的位置关系可以用节点之间的最短路径 $\phi(vi,v_j):V \times V \to R$ 来表示(无关联的两个节点之间的最短路径为-1)。 函数 $\phi$ 可以由图中节点之间的连通性来定义。在这篇文章中作者选用的是最短路径长度SPD。并进行可学习参数映射为 $b{\phi(v_i,v_j)}$ ,在所有层之间共享。
将这一特征融入注意力矩阵,使得注意力系数也包含了图中节点的相对位置(连接关系)信息:
这样做的好处:
- 首先,与传统GNN相比,其中接受场仅限于邻居,可以在公式中看到这一点。transformer层提供了全局信息,每个节点都可以关注图中的所有其他节点。
- 其次,通过使用 $b_{\phi(v_i,v_j)}$,单个transformer层中的每个节点可以根据图的结构信息自适应地关注所有其他节点。比如学到的b是个单调减函数,那就表达了最短路径越大的节点之间的关系越小,这也是图神经网络中的基本思想:越近的邻居的信息越重要。
注意力层面 Edge Encoding in the Attention
此外,graph相关的任务中通常还有边的信息,这些特征对于图形表示很重要。
以前工作中的有两种编码方式:
- 在第一种方法,边缘特征被添加到关联节点的特征。
- 在第二种方法,对于每个节点,其关联边的特征将与节点特征一起aggregation使用。
但这种使用边特征的方法只将边信息传播到其关联的节点,这可能不是利用边信息来表示整个图的有效方式。
作者提出了一个新的edge编码方式,
注意机制需要估计每个节点对 $(vi,v_j)$ 的相关性,作者认为应该在相关性中考虑连接它们的边 (像多跳图网络那样)。对于每个有序节点对 $(v_i,v_j)$,从 $v_i$ 到 $v_j$ 的最短路径为 $SP{ij}=(e_1,e_2,…,e_n)$,则可以用路径的加权平均得到两个节点之间边的相关信息:
其中 $x_{e_n}$ 是第n个边 $e_n$ 的特征,$w_n^E \in R^{d_E}$ 是第n个权重embedding,$d_E$ 是边特征的维度。
将这个信息也一起融入到注意力机制中:
1 | # Scaled Dot-Product Attention. |
把 $A_{ij}$ 的三部分进行拆分,三个分支的网络分别学习不同层面的信息,然后再后面再对三个分支的网络输出进行concat或者attention是否有帮助?
图池化的一个细节
想要表示图级别的embedding,Graphormer采用了一个额外写的特殊节点 $[VNode]$ , 让它和图中每个节点都链接。
有点像bert中的CLS一样,整个图$h_G$的表示将是最终层中的 $[VNode]$ 的节点特征
Do these modifications make Graphormer more powerful than other GNN variants?
Fact 1.
通过选择合适的权值和距离函数 $\phi$,Graphormer layer可以表示GIN、GCN、GraphSAGE等流行的广义网络模型的AGGREGATE和 COMBINE 步骤。
- Spatial encoding 使得 self-attention 模块能够区分节点 $v_i$ 的邻居集合 $N(v_i)$,从而SoftMax函数可以计算 $N(v_i)$ 上的平均统计量
- 通过了解节点的度,平均邻域可以转化为邻域之和
- 利用多头注意力和FFN,可以分别处理 $v_i$ 和 $N(v_i)$ 的表示,并且将其组合在一起。
证明1
采用空间编码的自我注意模块可以表示均值聚合
如果 $\phi=1$ ,则设置 $b{\phi}=0$ ,否则设置 $b{\phi}=−∞$,其中 $\phi$ 是 SPD。意思是如果直接相连就考虑其原本的注意力分数,如果不是直接相连注意力分数就为负无穷,就和普通的GNN一样的了。
设置 $W_Q=W_K=0$ 且 $W_V$ 为单位矩阵,$softmax(A)V$ 表示邻居表示的平均值。
实验
OGB-LSC quantum chemistry regression (i.e., PCQM4M-LSC) challenge
这是目前最大的图形级预测数据集,总共包含超过380万个图表
还有其他三个任务:ogbg- molhiv, ogbg-molpcba and ZINC
主要有两种模型大小:
Graphormer (L = 12, d = 768) , $Graphormer_{SMALL}$ (L = 6,d = 512).
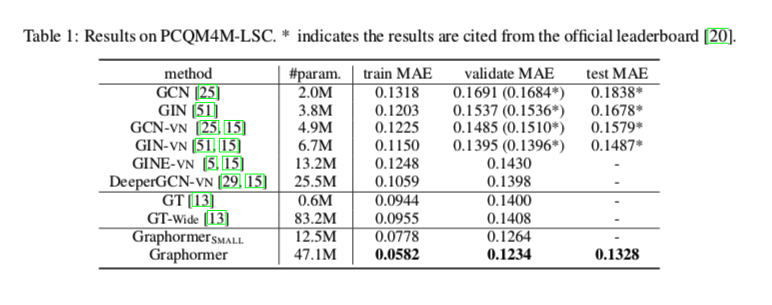
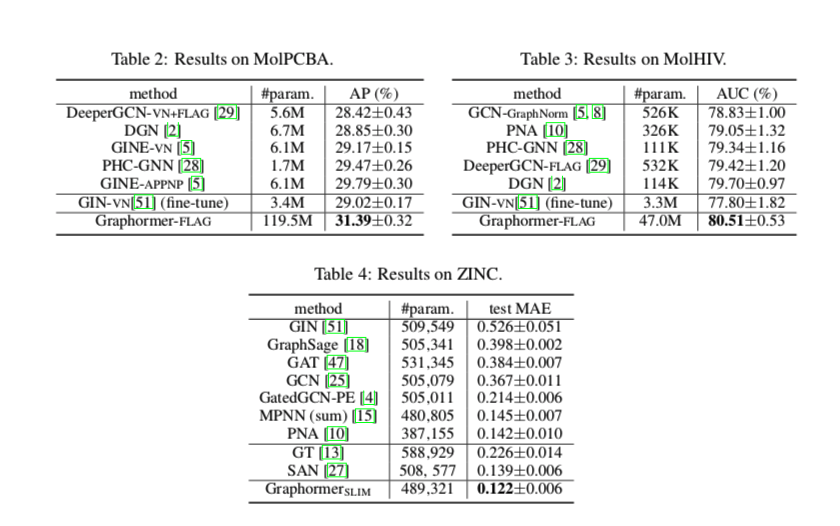
消融实验
将以前使用的位置编码(PE)与作者提出的空间编码进行了比较,这两种编码的目的都是对变压器的不同节点关系信息进行编码。
以前的基于变压器的GNN采用了各种PE,例如Weisfeiler-Lehman-PE(WL-PE)和Laplacian PE。采用的是Laplacian ,有文章证明一系列PE相比,它的性能很好。
采用空间编码的transformer体系结构的性能优于基于位置编码的transformer体系结构,说明了利用空间编码捕获节点空间信息的有效性。








