Meta Learning(李宏毅)
Meta Learning
李宏毅:https://www.bilibili.com/video/BV15b411g7Wd?p=57&spm_id_from=pageDriver
一个不错的科普:https://www.bilibili.com/video/BV1KB4y1c7gg?from=search&seid=2922012165894972973
什么是元学习
Meta Learning = Learn to Learn (学习如何去做学习这件事)
机器在学习了很多task后,在获得过去的任务下所汲取的经验后,学习到了更多的学习技巧,成为了一个更厉害的学习者。
从而有一个新任务,他可以学的更快更好。
比如:task1你教机器去学语音识别,task2你教他去做图片识别,那么task3你让他去学习文字识别,那么他可能学的会更好。
元学习的输入是训练数据,输出的是可以用于下一个任务的function,function也就是万能函数模拟器神经网络的模型参数
其中F 代表元学习算法,D是数据,f就是function。理解下图:
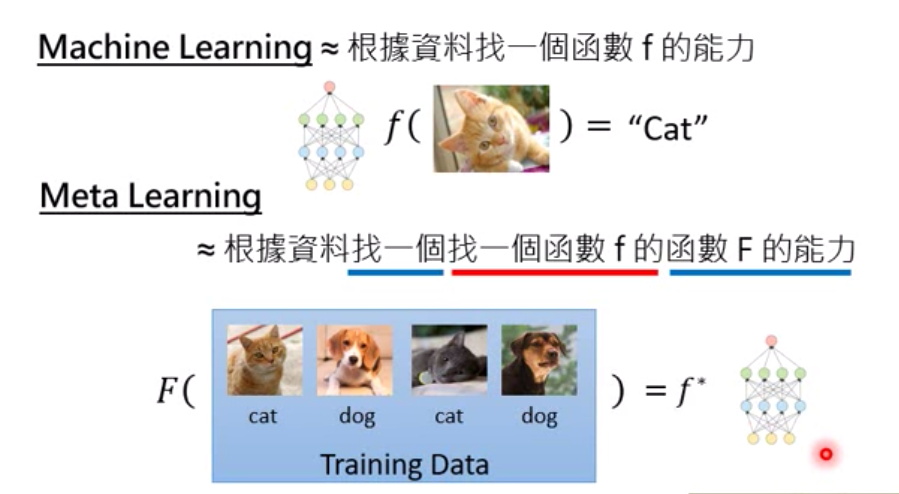
和机器学习的区别
机器学习:定义一系列function—->定一个function好坏的指标——-> 用gradient decent找到一个最好的function
元学习(也是找一个function):定义一系列大Function——->定一个评价大Function好坏的指标——->找到一个最好的大Function
和终身学习(Life-long learning)有些像?
持续/终身学习:是让同一个模型可以同时学会很多任务技能
而元学习是不同的任务仍然有不同的模型,我们期待的是模型通过以前的学习经历可以让他在未来别的任务上学的好。
元学习过程
定义一系列学习算法
为什么是一系列学习算法,其实不同的模型参数、不同的结构、不同的学习参数的组合都是不同的学习算法。
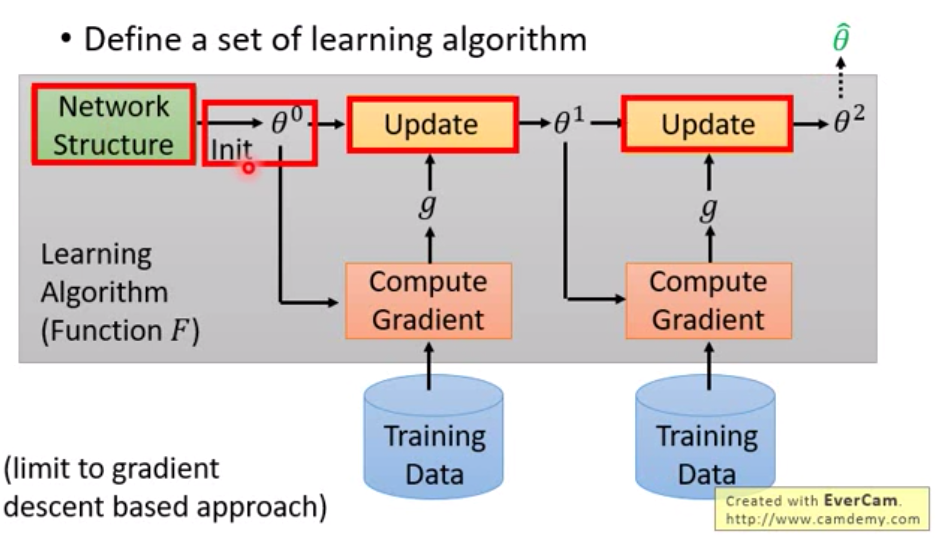
以梯度下降法为例,首先定义一个网络结构,初始化一个参数,通过训练数据计算一个梯度g,再通过学习率更新参数。
迭代多次最后得到最终参数$\hat \theta$
但上图中红色框框内的都是人为定义的。元学习就是想让这红框内的东西,不让人来设计,让机器根据先验知识来自己学习设计。
评估function参数好坏
让模型先学一些任务,去解一些问题看看。
比如Task1:用一些$D{train}$ 数据去训练模型得到$f_1$ ,再用Task1的$D{test}$ 去衡量 $f_1$ 得到一个loss $l_1$
一个任务不够,再多找些任务来
Task2:用一些$D{train}$ 数据去训练模型得到$f_2$ ,再用Task2的$D{test}$ 去衡量 $f_2$得到一个loss $l_2$
最后得到评价F好坏的Loss:
N 为任务数
meta learning 通常会把task的Train叫做Suppot set,Test叫做Query set
MAML(Model Agnostic Meta-Learning)
学一个初始化的参数
$\phi$ 输入的初始化参数,$\hat \theta^n$ 在第n个task上学出来的model,$\hat \theta^n$ 取决于$\phi$
$l^n(\hat \theta^n)$: 把$\hat \theta^n$这组参数拿到第n个task的测试集中去看看效果怎么样
怎么确定初始化的参数好不好,就用初始化参数到不同task上去做训练
最小化$L(\phi)$ : $\phi \gets \phi-\alpha ▽_{\phi}L(\phi)$
和迁移学习(Transfer learning) 预训练有些像?
迁移学习:某一个任务的数据很少,但另外一个任务的数据多。就把model预训练在多的数据上,再fine-tuning在少的数据上。
他的loss function:
在MAML里面loss是用$\phi$ 训练完后的model计算出来的,是训练过后的model
在pretrain里是用现在这个model直接去下游任务中衡量表现怎么样。
有的文章把预训练改成MAML的形式,以缓解预训练任务和下游任务直接目标不同产生的gap。
在MAML中,我们不在意$\phi$ 在training task上的表现,在意的是用$\phi$ 训练出来的$\hat \theta^n$的表现如何
(面向的是学习的过程,并不是学习的结果)
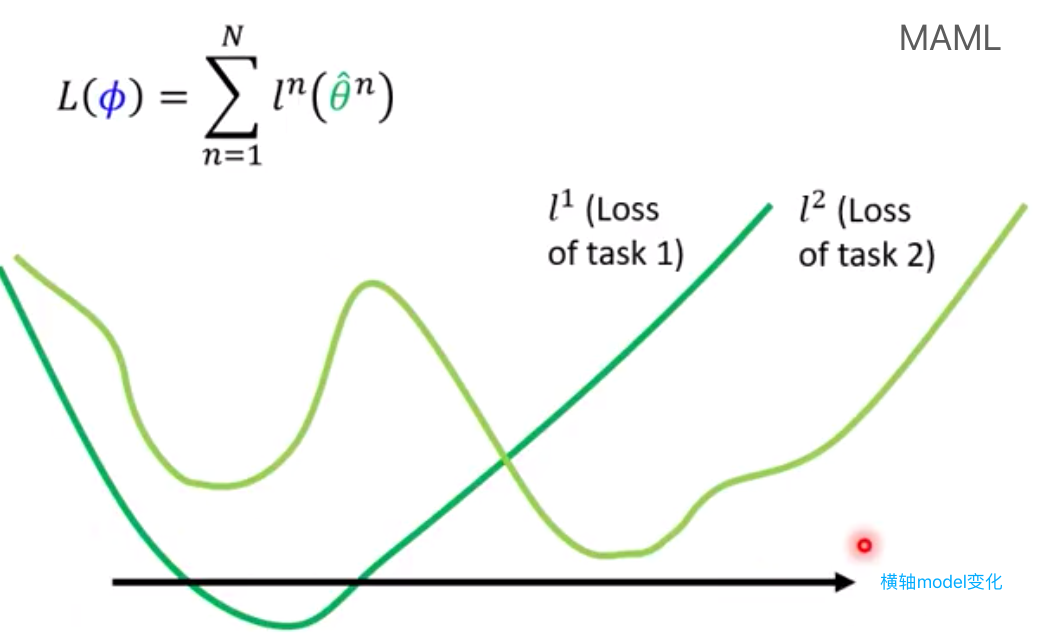
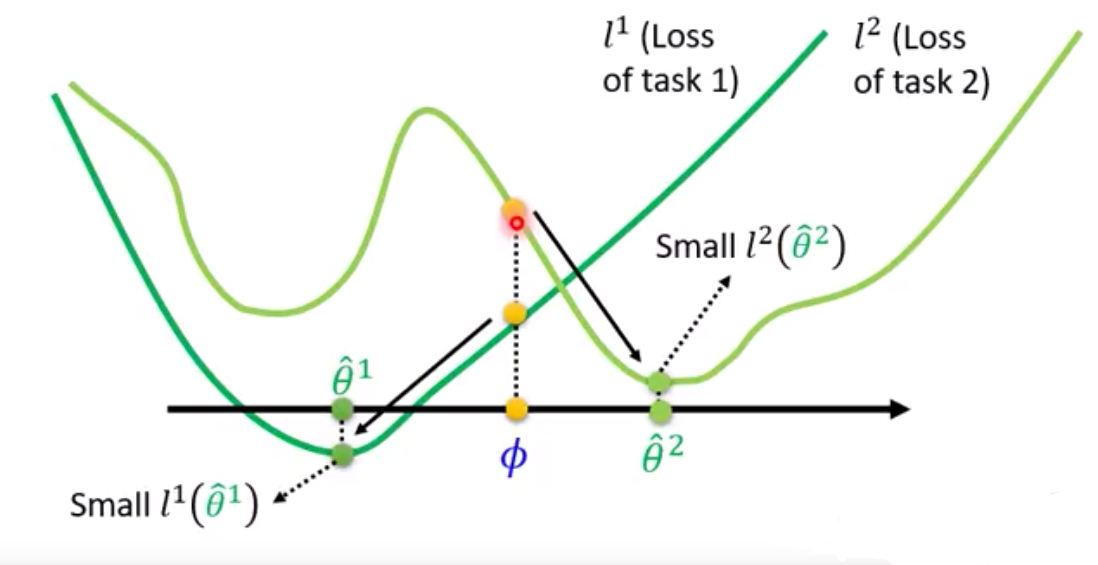
如上图虽然$\phi$ 本身表现不够好,但$\phi$经过训练以后可以变得很强 (潜力如何)
而pretrain在意的是现在这个$\phi$表现的怎么样,是在找寻在所有task都最好的$\phi$, 并不保证训练以后会得到好的 $ \hat \theta^n$ (现在表现如何)
并且MAML只训练很少的步数,因为
- 为了快速
- 希望在训练一步就得到很好的结果
- 在使用算法模型时可以多update
- 为了适应Few-shot learning
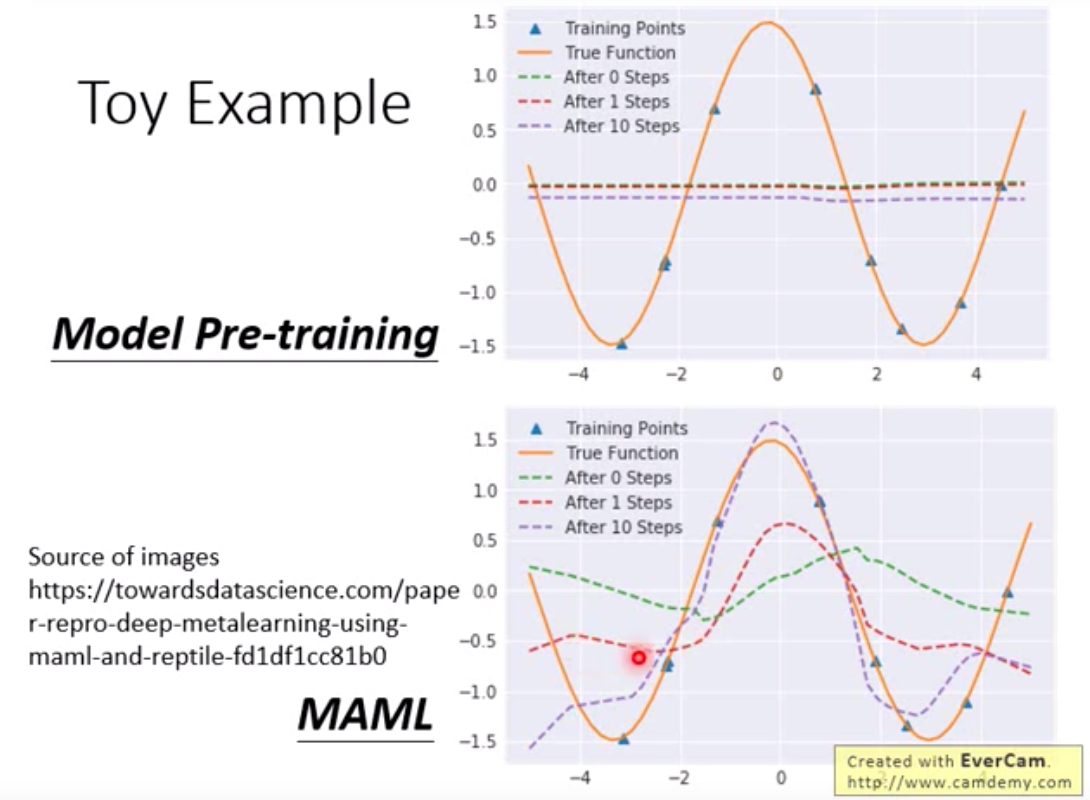
Toy Example
每一个任务:
- 给一个目标sin函数 $y = a sin(x+b)$ 其中 a、b 都是随机数,每一组 a、b 对应一条正弦曲线
- 从目标函数中采样k个点
- 使用采样点去估计目标函数
希望拟合的y越好越好。随机采样不同的a和b就可以得到不同的任务。