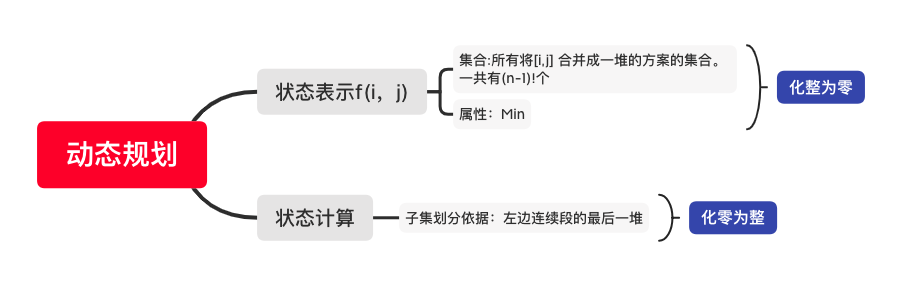
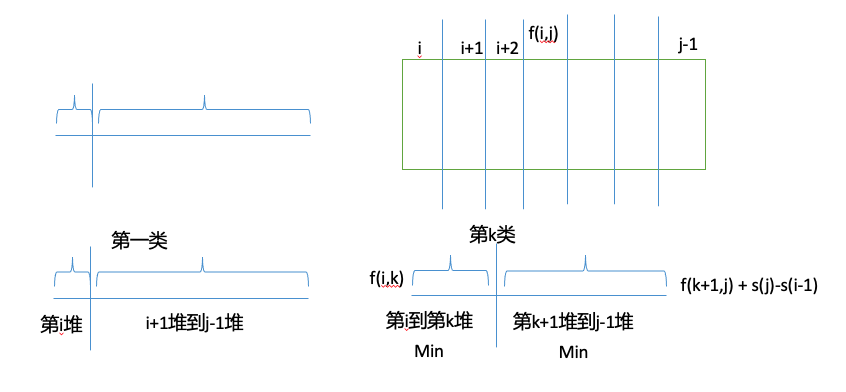
DP分析——石子合并
设有 NN 堆石子排成一排,其编号为 1,2,3,…,N。
每堆石子有一定的质量,可以用一个整数来描述,现在要将这 N 堆石子合并成为一堆。
每次只能合并相邻的两堆,合并的代价为这两堆石子的质量之和,合并后与这两堆石子相邻的石子将和新堆相邻,合并时由于选择的顺序不同,合并的总代价也不相同。
例如有 4 堆石子分别为 1 3 5 2, 我们可以先合并 1、2堆,代价为 4,得到 4 5 2, 又合并 1,2 堆,代价为 9,得到 9 2 ,再合并得到 11,总代价为 4+9+11=244+9+11=24;
如果第二步是先合并 2,3 堆,则代价为 7,得到 4 7,最后一次合并代价为 11,总代价为 4+7+11=22。
问题是:找出一种合理的方法,使总的代价最小,输出最小代价。
输入格式
第一行一个数 N 表示石子的堆数 N。
第二行 N 个数,表示每堆石子的质量(均不超过 1000)。
输出格式
输出一个整数,表示最小代价。
数据范围
1≤N≤300 1≤N≤300
输入样例:
输出样例:
解
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
| public class DP_石子合并 {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int N = scanner.nextInt();
int[] s = new int[N + 1];
for (int i = 1; i <= N; i++) {
s[i] = scanner.nextInt();
s[i] += s[i - 1];
}
int[][] dp = new int[N + 1][N + 1];
for (int len = 2; len <= N; len++) {
for (int i = 1; i + len - 1 <= N; i++) {
int j = i + len - 1;
dp[i][j] = 100000000;
for (int k = i; k < j; k++) {
dp[i][j] = Math.min(dp[i][j], dp[i][k] + dp[k + 1][j] + s[j] - s[i - 1]);
}
}
}
System.out.println(dp[1][N]);
}
}
|
$O(n^3)$
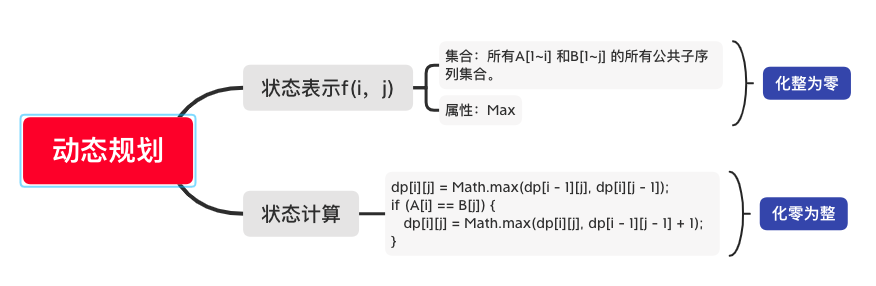
最长公共子序列
给定两个长度分别为 N 和 M 的字符串 A 和 B,求既是 A 的子序列又是 B 的子序列的字符串长度最长是多少。
输入格式
第一行包含两个整数 N 和 M。
第二行包含一个长度为 N 的字符串,表示字符串 A。
第三行包含一个长度为 M 的字符串,表示字符串 B。
字符串均由小写字母构成。
输出格式
输出一个整数,表示最大长度。
数据范围
1≤N,M≤1000 1≤N,M≤1000
输入样例:
输出样例:
解
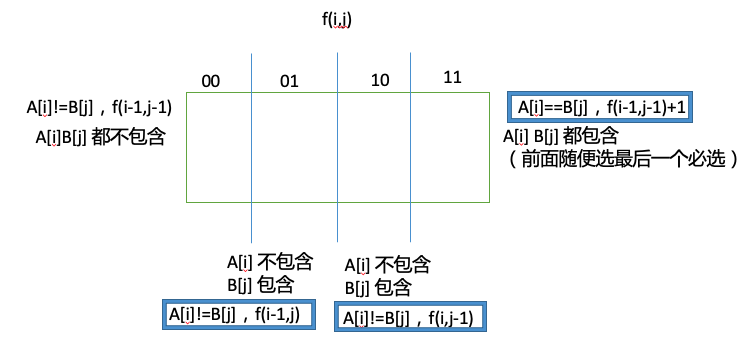
最坏情况下 aaaa,aaaaa,A中所有都是由 $2^n$ 个不同子序列。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
| public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int N = scanner.nextInt();
int M = scanner.nextInt();
String strA = " " + scanner.next();
String strB = " " + scanner.next();
int[][] dp = new int[N + 1][M + 1];
for (int i = 1; i <= N; i++) {
for (int j = 1; j <= M; j++) {
dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
if (strA.charAt(i) == strB.charAt(j)) {
dp[i][j] = Math.max(dp[i][j], dp[i - 1][j - 1] + 1);
}
}
}
System.out.println(dp[N][M]);
}
|