Auto-Encoding Variational Bayes

在存在后验分布难以处理的连续隐变量和大数据集的情况下，我们如何在有向概率模型中进行有效的推理和学习？我们介绍了一种随机变分推理和学习算法，该算法可以扩展到大型数据集，在一些温和的可分性条件下，甚至可以在难以解决的情况下工作。

我们的贡献有两个方面。首先，我们表明，变分下限的重新参数化产生了一个下限估计器，可以使用标准的随机梯度方法直接优化。其次，我们表明，对于每个数据点具有连续潜变量的i.i.d.数据集，通过使用提议的下限估计器将近似推理模型（也称为识别模型）拟合到难以解决的后验中，可以使后验推理特别有效。理论上的优势反映在实验结果中。

Introduction

如何才能对连续隐变量和/或参数具有难以处理的后验分布的有向概率模型进行有效的近似推理和学习？

变分贝叶斯(VB)方法涉及对难以处理的后验的近似进行优化。不幸的是，常见的均值场方法需要对近似后验的期望值进行分析解，这在一般情况下也是难以解决的。

我们展示了变分下限的重新参数化如何产生一个简单的可微分的无偏估计器；这个SGVB（随机梯度变分贝叶斯）估计器可用于几乎任何具有连续隐变量和/或参数的模型中的有效近似后验推断，并且使用标准随机梯度上升技术直接优化。

对于一个独立的数据集和每个数据点的连续隐变量的情况，我们提出了自编码VB（AEVB）算法。在AEVB算法中，我们通过使用SGVB估计器来优化识别模型，使推理和学习特别有效，这使我们能够使用简单的祖先采样进行非常有效的近似后验推理，这反过来又使我们能够有效地学习模型参数，而不需要每个数据点的昂贵迭代推理方案（如MCMC）。学习到的近似后验推理模型也可以用于一系列的任务，如识别、去噪、表示和可视化的目的。当一个神经网络被用于识别模型时，我们就得到了变量自编码器。

Method

本节中的策略可用于为具有连续隐变量的各种有向图模型推导下界估计量（随机目标函数）。我们将在这里限制自己具有 i.i.d 的常见情况。 每个数据点具有潜在变量的数据集，我们喜欢对（全局）参数执行最大似然（ML）或最大后验（MAP）推断，以及对潜在变量进行变分推断。

例如，可以直接将此场景扩展到我们还对全局参数执行变分推理的情况； 该算法放在附录中，但该案例的实验留给未来的工作。请注意，我们的方法可以应用于在线的非静态设置，例如 流数据，但这里为了简单起见，我们假设一个固定的数据集。

Problem scenario

让我们考虑一些数据集 $X={x^{(i)}}_{i=1}^N$ , 由一些连续或离散变量 $x$ 的 N 个 i.i.d 样本组成。我们假设数据是由某个随机过程产生的，涉及一个未观测到的连续随机变量 $z$。

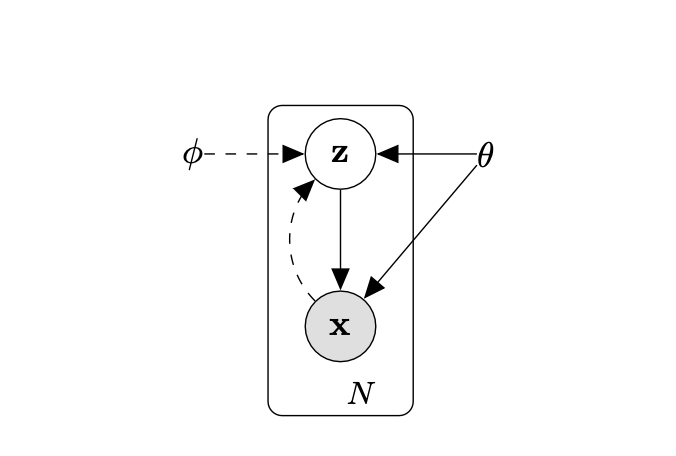
图1.正在考虑的有向图模型的类型。实线表示生成模型 $pθ(z)pθ(x|z)$，虚线表示变分逼近 $q{\phi}(z|x)$ 到难以处理的后验 $pθ(z|x)$。 变分参数 $\phi$ 与生成模型参数 $θ$ 共同学习。

该过程由两个步骤组成：

• 从某个先验分布 $p_{θ^*}(z)$生成值 $z^{(i)}$；
• 从某个条件分布 $p_{θ^*}(x|z)$ 生成值 $x^{(i)}$。

我们假设先验 $p{θ^∗}(z)$ 和似然 $p{θ^∗}(x|z)$ 来自分布 $pθ(z)$ 和 $pθ(x|z)$ 的参数族，并且它们的 PDFs 几乎在任何地方都是可微的 w.r.t. $θ$ 和 $z$。不幸的是，很多这个过程在我们看来是隐藏的：我们不知道真正的参数 $θ^∗$ 以及隐变量 $z^{(i)}$ 的值。

非常重要的是，我们不对边际或后验概率做出常见的简化假设。 相反，我们在这里对一种通用算法感兴趣，该算法甚至在以下情况下也能有效工作：

1. 难处理性：边际似然 $p{\theta} = \int p{\theta}(z)p{\theta}(x|z)dz$ 的积分难以处理的情况（因此我们无法评估或区分边际似然），其中真实的后验密度 $p{\theta}(z|x) = p{\theta}(x|z)p{\theta}(z)/p{\theta}(x)$ 是难以处理的（因此不能使用 EM 算法），并且任何合理的平均场 VB 算法所需的积分也是难以处理的。这些难以处理的问题非常普遍，并且出现在中等复杂的似然函数 $p{\theta}(x|z)$ 的情况下，例如 具有非线性隐藏层的神经网络。
2. 大型数据集：我们有太多的数据，以至于批量优化成本太高； 我们希望使用小批量甚至单个数据点进行参数更新。 基于采样的解决方案，例如 Monte Carlo EM 通常会太慢，因为它涉及每个数据点通常昂贵的采样循环。

我们对上述场景中的三个相关问题感兴趣，并提出解决方案：

1. 参数 $θ$ 的有效近似 ML 或 MAP 估计。 参数本身可能是感兴趣的，例如 如果我们正在分析一些自然过程。 它们还允许我们模拟隐藏的随机过程并生成类似于真实数据的人工数据。
2. 给定观察值 $x$ 以选择参数 $θ$，对隐变量 $z$ 进行有效的近似后验推断。 这对于编码或数据表示任务很有用。
3. 变量 $x$ 的有效近似边际推断。 这使我们能够执行需要先验 $x$ 的各种推理任务。 计算机视觉中的常见应用包括图像去噪、修复和超分辨率。

为了解决上述问题，让我们引入一个识别模型 $q{\phi }(z|x)$：一个对难以解决的真实后验 $p{θ}(z|x)$的近似。请注意，与均值场变分推理中的近似后验相比，它不一定是因果关系，它的参数 $\phi $ 也不是由某种闭合形式的期望值计算出来的。相反，我们将引入一种方法来学习识别模型参数 $\phi$ 和生成模型参数 $\theta$。

从编码理论的角度来看，未观察到的变量 $z$ 可以解释为一种潜在的表示或代码。因此，在本文中，我们也将把识别模型 $q{\phi }(z|x)$ 称为概率编码器，因为给定一个数据点 $x$ ，它产生一个关于编码 $z$ 的可能值的分布（例如高斯），数据点 $x$ 可能是由此产生的。类似地，我们将把 $pθ(x|z)$ 称为概率解码器，因为给定一个编码 $z$，它产生一个关于 $x$ 的可能对应值的分布。

The variational bound

边际似然由单个数据点的边际似然之和 $\log p{\theta}(x^{(1)},…,x^{(N)}) = \sum{i=1}^{N} \log p_{\theta}(x^{(i)})$ 组成，每个数据点可以改写为：

$$\log p_{\theta}(x^{(i)}) = D_{KL}(q_{\phi}(z|x^{(i)}) || p_{\theta}(z|x^{(i)})) + L(\theta,\phi;x^{(i)})$$

第一个 RHS 项是近似值与真实后验的 KL 散度。 由于这个 KL 散度是非负的，第二个 RHS 项 $L(\theta,\phi,x^{(i)})$ 被称为数据点 $i$ 的边际似然的（变分）下界，可以写成：

$$log p_{\theta}(x^{(i)}) \ge L(\theta,\phi;x^{(i)}) = E_{q_{\phi}(z|x^{(i)})}[\log p_{\theta}(x^{(i)}|z)]$$

也可以写成：

$$L(\theta,\phi;x^{(i)}) = - D_{KL}(q_{\phi}(z|x^{(i)}) || p_{\theta}(z)) + E_{q_{\phi}(z|x^{(i)})}[\log p_{\theta}(x^{(i)}|z)]$$

我们想要区分和优化下界 $L(θ,\phi;x(i))$ w.r.t 变分参数 $\phi $ 和生成参数 $θ$。然而，下界 w.r.t $\phi$ 的梯度有点问题。 这类问题的常用（näıve）蒙特卡洛梯度估计器是：$\nabla{\phi} E{q{\phi}(z)}[f(z)] = E{q{\phi}(z)}[f(z)\nabla{q{\phi}(z)}\log q{\phi}(z)] \simeq \frac{1}{L}\sum{l=1}^{L} f(z) \nabla{q{\phi}(z^{(l)}) }\log q{\phi}(z^{(l)})$ 其中 $z^{(l)}\sim q_{\phi}(z|x^{(i)})$ 这个梯度估计器表现出非常高的方差（参见例如 [BJP12]），对于我们的目的来说是不切实际的。

The SGVB estimator and AEVB algorithm

在这一节中，我们将介绍一个实用的下限及其导数（相对于参数）的估计器。我们假设 $q{\phi }(z|x)$ 形式的近似后验，但请注意，该技术也可以应用于 $q{\phi}(z)$ 的情况，即我们不以 $x$ 为条件。用于推断参数后验的完全变异贝叶斯方法在附录中给出。

在第 2.4 节中概述的某些温和条件下，对于选择的近似后验 $q{\phi }(z|x)$，我们可以使用（辅助）噪声的可微变换 $g{\phi}(ε, x)$ 重新参数化随机变量 $\hat z \sim q_{\phi}(z|x)$ 变量 $ε$：

$$\hat z = g_{\phi}(\epsilon , x) \ with \epsilon \sim p(\epsilon)$$

关于选择这种合适的分布 $p(\epsilon)$ 和函数 $g{\phi}(ε,x)$ 的一般策略，见2.4节。现在我们可以对一些函数 $f(z)$ 的期望值进行蒙特卡洛估计，即 $q{\phi}(z|x)$，具体如下:

$$E_{q_{\phi}(z|x^{(i)})} [f(z)] = E_{p(\epsilon)}[f(g_{\phi}(\epsilon, x^{(i)}))] \simeq \frac{1}{L} \sum_{l=1}^{L} f(g_{\phi}(\epsilon^{(l)}, x^{(i)})) \ \ where \ \ \epsilon^{(l)}\sim p(\epsilon)$$

我们将这一技术应用于变分下限（公式（2）），产生我们的通用随机梯度变分贝叶斯（SGVB）估计器 $\hat L^A(\theta, \phi; x^{(i)}) \simeq L(\theta, \phi;x^{(i)})$:

$$\hat L^A(\theta, \phi; x^{(i)}) = \frac{1}{L}\sum_{l=1}^L\log p_{\theta}(x^{(i)}, z^{(i,l)} ) - \log q_{\phi}(z^{(i,l)}| x^{(i)}) \\ where \ \ z^{(i,l)} = g_{\phi}(\epsilon^{i,l}, x^{(i)}) \ and \ \epsilon^{(l)} \sim p(\epsilon)$$

通常，公式(3)的 KL散度 $D{KL}(q{\phi}(z|x^{(i)})||p{\theta}(z))$ 可以用分析法进行积分(见附录B)，这样，只有预期重建误差$E{q{\phi}(z|x^{(i)})}\log p{\theta}(x^{(i)}|z)$ 需要通过抽样进行估计。
然后可以将 KL 散度项解释为正则化 $\phi$ ，鼓励近似后验接近先验 $p_{\theta}(z)$。这产生了 SGVB 估计器的第二个版本 $\hat L^B(\theta,\phi;x^{(i)}) \simeq L(\theta,\phi;x^{(i)})$，对应于等式(3)，它的方差通常比通用估计量小：

$$\hat L^B(\theta, \phi; x^{(i)}) = -D_{KL}(q_{\phi}(z|x^{(i)}) || p_{\theta}(z)) + \frac{1}{L}\sum_{l=1}^L(\log p_{\theta}(x^{(i)}|z^{(i,l)}))\\ where \ \ \ z^{(i,l)} = g_{\phi} (\epsilon^{(i,l)}, x^{(i)}) \ and \ \epsilon^{(l)}\sim p(\epsilon)$$

给定来自具有 $N$ 个数据点的数据集 $X$ 的多个数据点，我们可以基于小批量构建完整数据集的边际似然下限的估计器：

$$L(\theta,\phi; X) \simeq \hat L^M(\theta, \phi;X^M) = \frac{N}{M} \sum_{i=1}^M\hat L(\theta,\phi;x^{(i)})$$

其中 minibatch $X^M = {x^{(i)}}^M_{i=1}$ 是从具有 $N$ 个数据点的完整数据集 $X$ 中随机抽取的 $M$ 个数据点样本。

在我们的实验中，我们发现每个数据点的样本数量 $L$ 可以设置为 1，只要 minibatch 大小 $M$ 足够大，例如 $M = 100$。可以取导数 $∇_{θ,\phi}\hat L(\theta;X^M)$，得到的梯度可以与 SGD 或 Adagrad [DHS10] 等随机优化方法结合使用。 有关计算随机梯度的基本方法，请参见算法 1。

查看等式给出的目标函数时，与自编码器的联系变得清晰。 (7)。 第一项是（近似后验与先验的 KL 散度）充当正则化项，而第二项是预期的负重构误差。选择函数 $g{\phi}(.)$ 使其将数据点 $x^{(i)}$ 和随机噪声向量 $ε^{(l)}$ 映射到来自该数据点的近似后验的样本：$z^{(i,l)} = g{\phi}(ε^{(l)}, x^{(i)})$ 其中 $z^{(i,l)} \sim q{\phi}(z|x^{(i)})$。随后，样本 $z^{(i,l)}$ 被输入到函数 $\log p{\theta}(x^{(i)}|z^{(i,l)})$，它等于生成条件下数据点 $x^{(i)}$ 的概率密度（或质量） 模型，给定 $z^{(i,l)}$。 该术语是自编码器用语中的负重构误差。

The reparameterization trick

为了解决我们的问题，我们调用了另一种方法来从 $q_{\phi}(z|x)$ 生成样本。 基本的参数化技巧非常简单。

令 $z$ 为连续随机变量，$z \sim q{\phi}(z|x)$ 为某个条件分布。 然后通常可以将随机变量 $z$ 表示为确定性变量 $z = g{\phi}(ε,x)$，其中 $\epsilon$ 是具有独立边际 $p(\epsilon) $ 的辅助变量，而 $g{\phi}(.)$ 是由$\phi$参数化的某个向量值函数 。这种重新参数化对我们的情况很有用，因为它可以用来重写期望 w.r.t $q{\phi}(z|x)$，使得期望的蒙特卡罗估计值是可微的 w.r.t φ。 证明如下。

这种重新参数化对我们的情况很有用，因为它可以用来重写期望 w.r.t $q_{\phi }(z|x)$，使得期望的蒙特卡罗估计值是可微的 w.r.t φ。

证明如下。 给定确定性映射 $z = g{\phi} (\epsilon, x)$ 我们知道 $z = g{\phi}(z|x)\prod_i dz_i =p(\epsilon)\prod_i d\epsilon_i$。

因此，$\int q{\phi}(z|x)f(z) dz = \int p(\epsilon)f(z)d{\epsilon} = \int p(\epsilon) f(g{\phi}(\epsilon,x)) d\epsilon$ 。因此可以构造一个可微的估计量：$\int q{\phi}(z|x)f(z)dz \simeq \frac{1}{L}f(g{\phi}(x,\epsilon^{(l)}))$ 其中 $\epsilon^{(l)}\sim p(\epsilon)$ 。在第2.3节中，我们应用这个技巧得到了变分下界的一个可微估计。

以单变量高斯情况为例：令 $z\sim p(z|x) = N(\mu, \sigma^2)$ 。在这种情况下，有效的重新参数化是 $z=μ+σ\epsilon$，其中ε是辅助噪声变量 $ε\sim N(0,1)$。因此 $E{N(z;\mu,\epsilon^2)} [f(z)] = E{N(\epsilon;0,1)}[f(\mu +\sigma\epsilon )] \simeq \frac{1}{L}\sum{l=1}^L f(\mu+\sigma\epsilon^{(l)})$, 其中 $\epsilon^{(l)}\sim N(0,1)$。对于其中的 $q{\phi }(z|x)$，我们可以选择这样的可微变换 $g_{\phi }(.)$ 和辅助变量 $\epsilon \sim p(\epsilon)$？三种基本方法是：

1. 易处理的逆 CDF。 在这种情况下，令 $\epsilon \sim U(0,I)$ ，令 $g{\phi }(ε,x)$ 为 $q{\phi }(z|x)$ 的逆 CDF。 示例：指数、Cauchy、Logistic、Rayleigh、Pareto、Weibull、倒数、Gompertz、Gumbel 和 Erlang 分布。
2. 与高斯示例类似，对于任何“location-scale”分布族，我们可以选择标准分布（位置 = 0，尺度 = 1）作为辅助变量 $ε$，并令 $g(.) = local + scale·ε$ . 示例：拉普拉斯分布、椭圆分布、学生 t 分布、逻辑分布、均匀分布、三角分布和高斯分布。
3. 组合：通常可以将随机变量表示为辅助变量的不同变换。 示例：Log-Normal（正态分布变量的取幂）、Gamma（指数分布变量的总和）、Dirichlet（Gamma 变量的加权和）、Beta、卡方和 F 分布。

当所有三种方法都失败时，存在对逆 CDF 的良好近似，需要计算的时间复杂度与 PDF 相当（参见例如 [Dev86] 中的某些方法）。

Example: Variational Auto-Encoder

在本节中，我们将给出一个示例，其中我们将神经网络用于概率编码器 $q{\phi} (z|x)$（生成模型 $p{\theta}(x, z)$ 的后验近似），其中参数 $\phi $ 和 $\theta $ 为 与AEVB算法联合优化。

让隐变量的先验为中心各向同性多元高斯 $p{\theta}(z) = N(z;0,I)$。请注意，在这种情况下，先验缺少参数。 我们让 $p{\theta} (x|z)$ 是一个多元高斯（在实值数据的情况下）或伯努利（在二进制数据的情况下），其分布参数是使用 MLP（一个全连接的神经网络 单个隐藏层，见附录 C)。

请注意，在这种情况下，真正的后验 $p{\theta}(z|x)$ 是难以处理的。 虽然 $q{\phi }(z|x)$ 的形式有很大的自由度，但我们将假设真实的（但难以处理的）后验采用具有近似对角协方差的近似高斯形式。 在这种情况下，我们可以让变分近似后验为具有对角协方差结构的多元高斯：

$$\log q_{\phi}(z|x^{(i)}) = \log N(z;\mu^{(i)}, \epsilon^{2(i)}I)$$

其中，近似后验值 $μ^{(i)}$和 $σ^{(i)} $的平均值和s.d.是编码MLP的输出，即数据点 $x^{(i)}$和变分参数 $\phi $ 的非线性函数（见附录C）。

如第2.4节所述，我们从后验 $z^{(i，l)} \sim q{\phi}(z|x^{(i)})$ 中采样，使用 $z^{(i,l)}=g{\phi}(x^{(i)}，ε^{(l)})=μ^{(i)}+σ^{(i)}\odot \epsilon ^{(l)}$，其中$ε^{(l)} \sim N(0,I)$。$\odot$ 表示元素乘积。 在这个模型中，$p{\theta }(z)$（先验）和 $q{\phi }(z|x)$ 都是高斯的； 在这种情况下，我们可以使用 eq.(7) 的估计器，其中 KL 散度可以在没有估计的情况下计算和微分（参见附录 B）。 该模型和数据点 $x^{(i)}$ 的结果估计量为：

$$L(\theta,\phi; x^{(i)}) \simeq \frac{1}{2}\sum_{j=1}^{J}(1+\log( (\sigma^{(i)}_j)^2 ) - (\mu_j^{(i)})^2 - (\sigma^{(i)}_j)^2)\\ where \ \ z^{(i,l)} = \mu^{(i)} + \sigma^{(i)} \odot \epsilon^{(l)} \ and \ \epsilon^{(l)}\sim N(0,I)$$

如上文和附录 C 所述，解码项 $\log p_{\theta} (x^{(i)} |z^{(i,l)} )$ 是伯努利或高斯 MLP，具体取决于我们建模的数据类型。

Related work

据我们所知，唤醒-睡眠算法 [HDFN95] 是文献中唯一适用于同一类连续潜变量模型的其他在线学习方法。 与我们的方法一样，wake-sleep 算法采用近似真实后验的识别模型。 唤醒睡眠算法的一个缺点是它需要同时优化两个目标函数，这两个目标函数一起不对应于边际似然的优化。 唤醒睡眠的一个优点是它也适用于具有离散隐变量的模型。 Wake-Sleep 与每个数据点的 AEVB 具有相同的计算复杂性。

随机变分推断 [HBWP13] 最近受到越来越多的关注。 最近，[BJP12] 引入了一种控制变量方案，以减少 2.1 节中讨论的朴素梯度估计器的高方差，并应用于后验的指数族近似。 在 [RGB13] 中，引入了一些通用方法，即控制变量方案，以减少原始梯度估计器的方差。 在 [SK13] 中，与本文类似的重新参数化被用于随机变分推理算法的有效版本中，用于学习指数族近似分布的自然参数。

AEVB 算法揭示了有向概率模型（用变分目标训练）和自动编码器之间的联系。 线性自编码器和某类生成线性高斯模型之间的联系早已为人所知。 在 [Row98] 中表明，PCA 对应于线性高斯模型特例的最大似然 (ML) 解，其中先验 $p(z) = N (0, I)$ 和条件分布 $p(x |z) = N (x; Wz, \epsilon I)$，特别是 ε 无限小的情况。

在最近关于自编码器 [VLL+10] 的相关工作中，表明非正则化自编码器的训练标准对应于输入 $X$ 和潜在之间的互信息的下限（参见 infomax 原则 [Lin89]）的最大化 表示 $Z$ 。互信息最大化（wrt参数）等价于最大化条件熵，其下限为自编码模型[VLL+10]下数据的预期对数似然，即负重构误差 .然而，众所周知，这种重建标准本身不足以学习有用的表示[BCV13]。已经提出了正则化技术来使自编码器学习有用的表示，例如去噪、收缩和稀疏自编码器变体 [BCV13]。 SGVB 目标包含一个由变分界规定的正则化项（例如 eq. (10)），缺少学习有用表示所需的通常令人讨厌的正则化超参数。相关的还有编码器-解码器架构，例如预测稀疏分解 (PSD) [KRL08]，我们从中汲取了一些灵感。同样相关的是最近引入的生成随机网络 [BTL13]，其中嘈杂的自动编码器学习从数据分布中采样的马尔可夫链的转换算子。在 [SL10] 中，一个识别模型被用于使用深度玻尔兹曼机器进行高效学习。这些方法要么针对非归一化模型（即像玻尔兹曼机这样的无向模型），要么仅限于稀疏编码模型，这与我们提出的用于学习一类有向概率模型的通用算法相反。

最近提出的 DARN 方法 [GMW13] 也使用自编码结构学习有向概率模型，但是他们的方法适用于二进制隐变量。 甚至最近，[RMW14] 还使用我们在本文中描述的重新参数化技巧在自动编码器、定向概率模型和随机变分推理之间建立了联系。 他们的工作是独立于我们开发的，并为 AEVB 提供了额外的视角。

Experiments

我们训练了来自 MNIST 和 Frey Face 数据集的图像生成模型，并在变分下限和估计的边际似然方面比较了学习算法。

使用了第 3 节中的生成模型（编码器）和变分近似（解码器），其中描述的编码器和解码器具有相同数量的隐藏单元。 由于 Frey Face 数据是连续的，我们使用了具有高斯输出的解码器，与编码器相同，只是在解码器输出处使用 sigmoidal 激活函数将均值限制在区间 (0, 1)。 请注意，对于隐藏单元，我们指的是编码器和解码器的神经网络的隐藏层。

使用随机梯度上升更新参数，其中梯度是通过区分下界估计量 $∇_{\theta,\phi} L(θ, \phi; X)$ 计算的（参见算法 1），加上对应于先验 $p(θ) = N(0,I)$ 的小权重衰减项 。 该目标的优化等效于近似 MAP 估计，其中似然梯度由下限的梯度近似。

我们将 AEVB 的性能与唤醒睡眠算法 [HDFN95] 进行了比较。 我们为唤醒睡眠算法和变分自编码器采用了相同的编码器（也称为识别模型）。 所有参数，无论是变分参数还是生成参数，都通过从 $N(0,0.01)$ 中随机抽样进行初始化，并使用 MAP 标准进行联合随机优化。 使用 Adagrad [DHS10] 调整步长； Adagrad 全局步长参数是根据前几次迭代中训练集的性能从 {0.01, 0.02, 0.1} 中选择的。 使用大小为 M = 100 的小批量，每个数据点 L = 1 个样本。

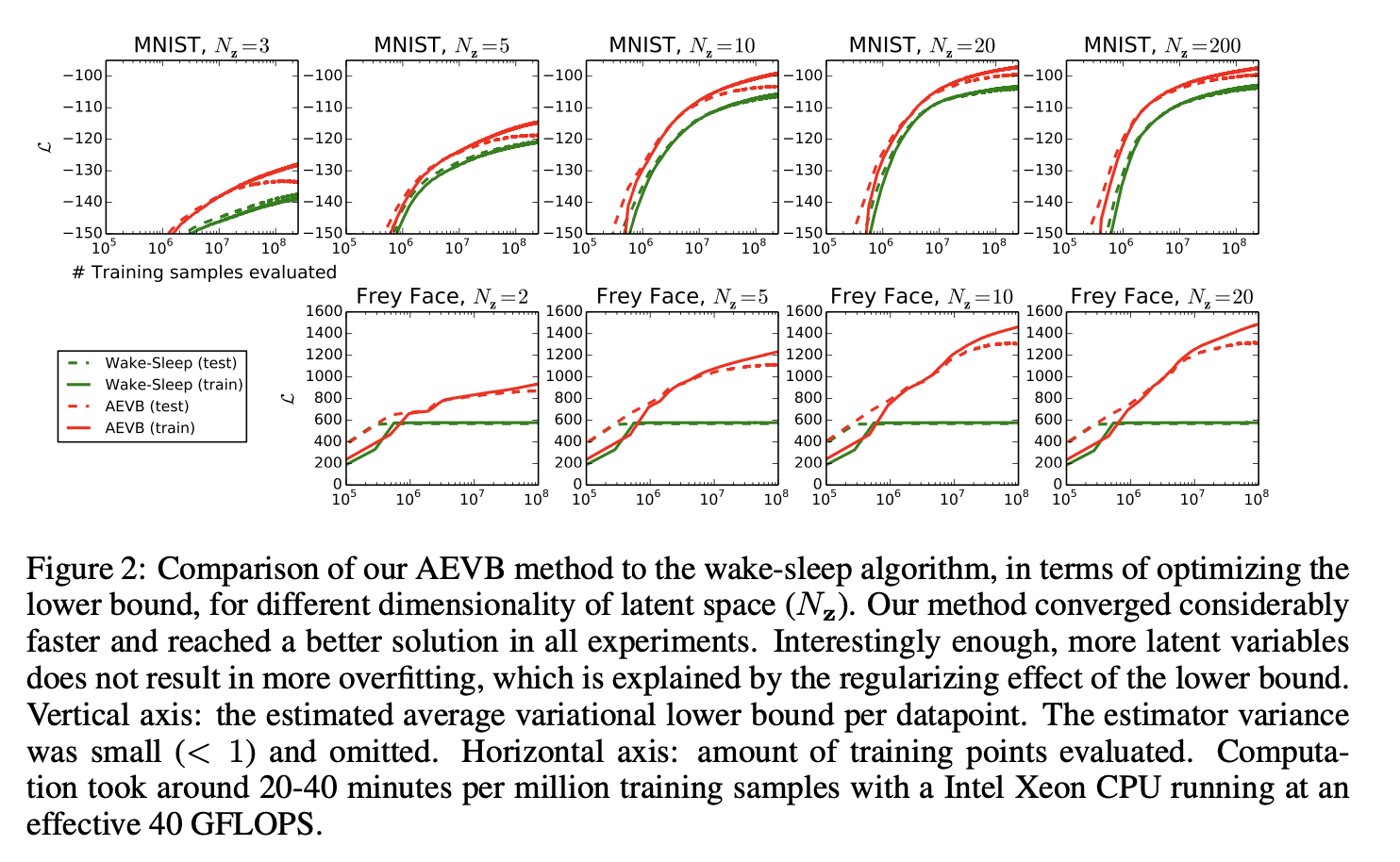
Likelihood lower bound 我们训练了生成模型（解码器）和相应的编码器（又名识别模型），在 MNIST 的情况下具有 500 个隐藏单元，在 Frey Face 数据集的情况下具有 200 个隐藏单元（以防止过度拟合，因为它是一个相当小的数据集）。 隐藏单元的选择数量是基于先前关于自编码器的文献，不同算法的相对性能对这些选择不是很敏感。 图 2 显示了比较下限时的结果。 有趣的是，多余的隐变量不会导致过拟合，这可以通过变分界的正则化性质来解释。

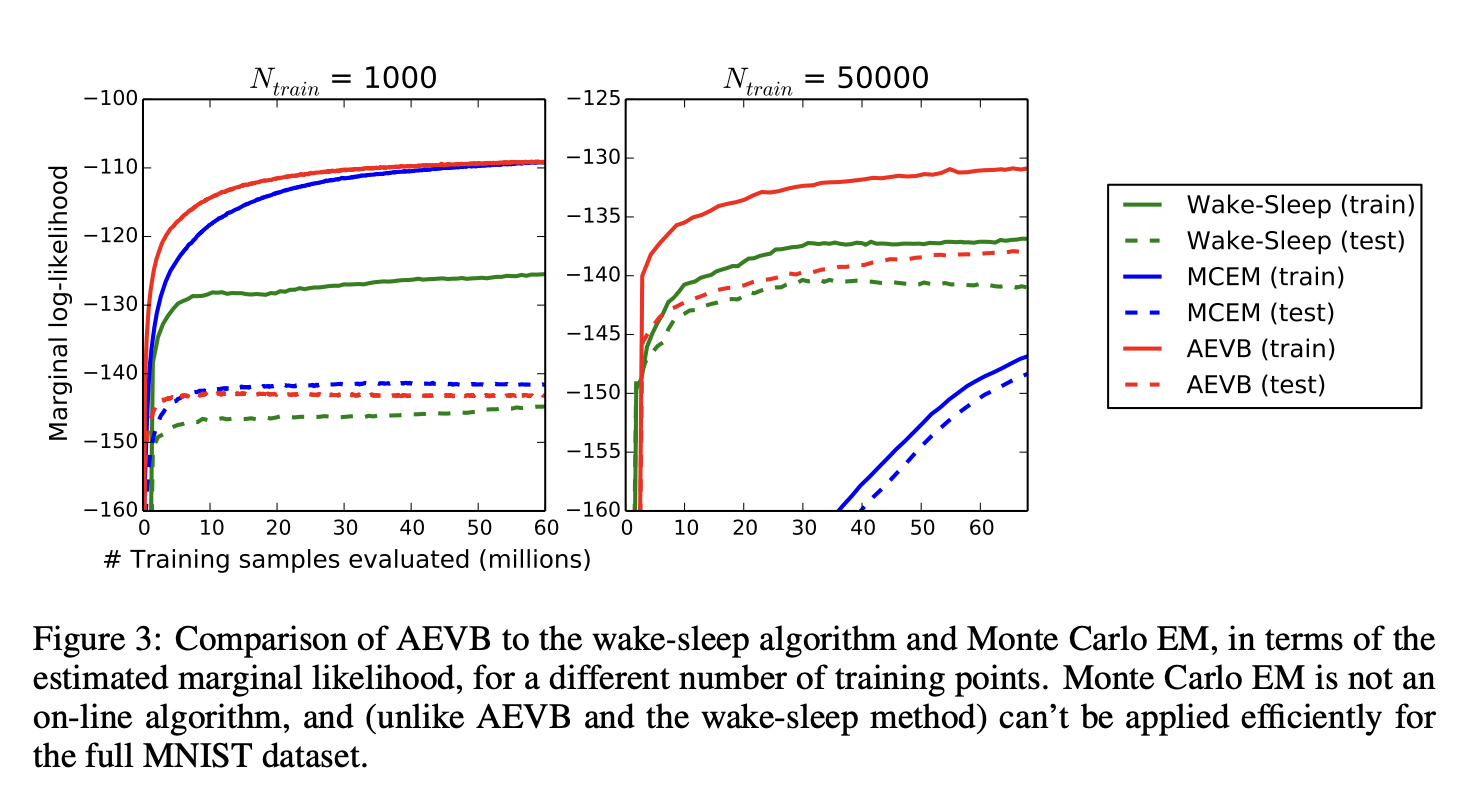
Marginal likelihood 对于非常低维的隐空间，可以使用 MCMC 估计器估计学习生成模型的边际似然。 有关边际似然估计量的更多信息，请参见附录。 对于编码器和解码器，我们再次使用了神经网络，这次有 100 个隐藏单元和 3 个隐变量； 对于更高维的潜在空间，估计变得不可靠。 同样，使用了 MNIST 数据集。 将 AEVB 和 Wake-Sleep 方法与具有混合蒙特卡罗 (HMC) [DKPR87] 采样器的蒙特卡罗 EM (MCEM) 进行了比较； 详细信息在附录中。 我们比较了三种算法的收敛速度，分别用于小型和大型训练集。 结果如图 3 所示。

Visualisation of high-dimensional data 如果我们选择低维潜在空间（例如 2D），我们可以使用学习到的编码器（识别模型）将高维数据投影到低维流形。 有关 MNIST 和 Frey Face 数据集的 2D 潜在流形的可视化，请参见附录 A。

Conclusion

我们引入了一种新的变分下界估计器，随机梯度 VB (SGVB)，用于使用连续潜在变量进行有效的近似推断。 所提出的估计器可以使用标准随机梯度方法直接区分和优化。 对于 i.i.d. 数据集和每个数据点的连续潜在变量 我们引入了一种高效的推理和学习算法，即自编码 VB (AEVB)，它使用 SGVB 估计器学习近似推理模型。 理论优势体现在实验结果中。

Future work

由于 SGVB 估计器和 AEVB 算法可以应用于几乎任何具有连续隐变量的推理和学习问题，因此有很多未来方向：

• 使用用于编码器的深度神经网络（例如卷积网络）学习分层生成架构 和解码器，与 AEVB 联合训练；
• 时间序列模型（即动态贝叶斯网络）；
• 将 SGVB 应用于全局参数；
• 具有隐变量的监督模型，可用于学习复杂的噪声分布。