Heterogeneous Graph Transformer for Graph-to-Sequence Learning

Graph2Seq学习的目的是将图结构的表示转换为单词序列，以便生成文本。

AMR-to-text是从抽象意义表示(AMR)图中生成文本的任务，其中节点表示语义概念，边表示概念之间的关系。

传统GNN只考虑了直接相连节点之间的关系，而忽略了远距离节点之间的间接关系。

Graph2Seq的其他两个和Graph Transformer的论文

• Graph transformer for graph-to-sequence learning AAAI 2020

• Modeling graph structure in transformer for better AMR-to-text gen- eration EMNLP 2019

使用节点之间的最短关系路径来编码语义关系。但是，它们忽略了关系路径中节点的信息，对直接关系和间接关系没有区别地进行编码。当从直接邻居那里聚集信息时，可能会干扰信息的传播过程。

作者使用Heterogeneous Graph Transformer来独立地建模原始图的各个子图中的不同关系，包括节点之间的直接关系、间接关系和多种可能的关系。

Input Graph Transformer

为了缓解语料库中的数据稀疏问题，作者将进一步将字节对编码(BPE)引入Levi图。

将原始节点拆分成多个子词节点。除了添加缺省连接外，我们还在子词之间添加了反向边和自循环边。

如下图：

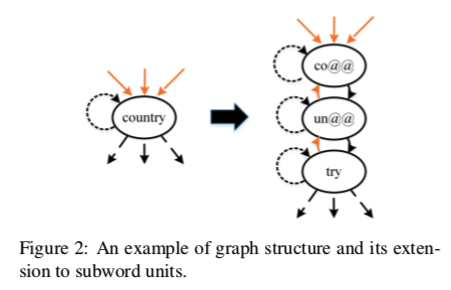
例如，图中的单词Country被分割为co@@、un@@、try 它们之间有三种类型的边。

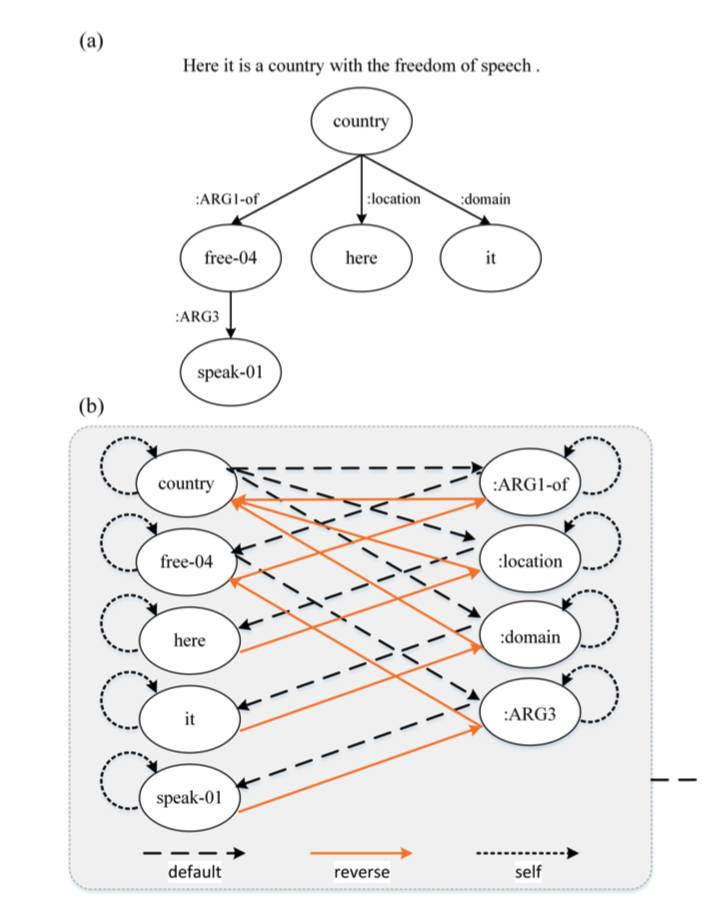
该任务一般先将抽象概念图(上图a)，转换成Levi图(上图b)。将AMR图转换为扩展的Levi图，该图可以看作是一个异构图，因为它具有不同类型的边。

Heterogeneous Graph Transformer

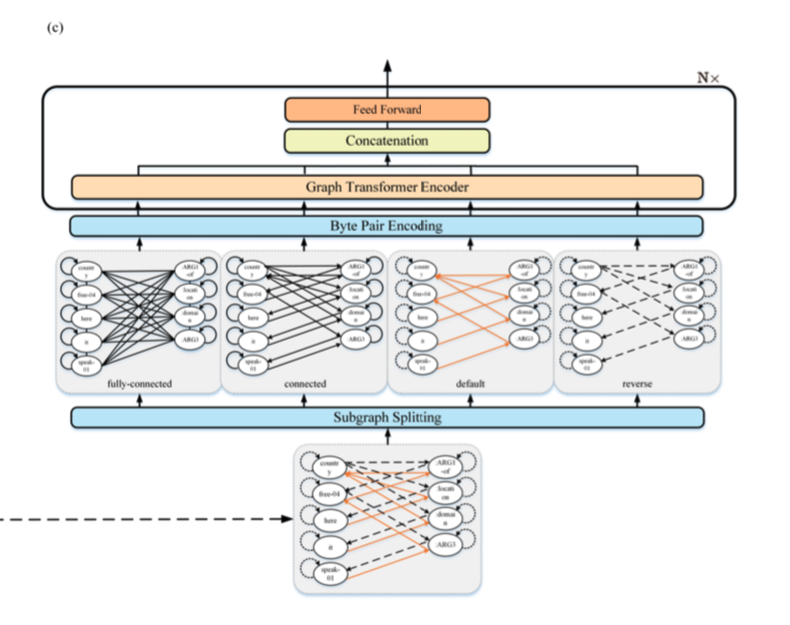
给定一个经过预处理的扩展Levi图，根据其异构性将扩展Levi图分成多个子图。

在每个Graph Encoder中，基于其在当前子图中的相邻节点来更新不同子图中的节点表示。然后，将该节点在不同子图中的所有表示组合在一起，以获得其最终表示。

Graph Encoder

与其他Graph Transformer不同的是仅使用相对位置编码来隐藏结构信息。

在更新每个节点的表示时，直接屏蔽了非相邻节点的注意力。mask attention $\alpha_{ij}\notin N_i$ ，此外这个作者还尝试用了加性注意力这就和GAT几乎很像了。

因此，给定输入序列 $x=(x_1,…,x_n)$，每个关注头中表示为 $z_i$ 的节点i的输出表示如下计算：

$$z_i = \sum_{j\in N_i} \alpha_{ij}(x_j W^V)$$

Heterogeneous Mechanism

在多头机制成功的激励下，提出了异质机制。考虑到一个句子，多头注意允许模型隐含地注意到来自不同位置的不同表示子空间的信息。相应地，异构机制使得模型显式地关注不同子图中的信息，对应于图的不同表示子空间，从而增强了模型的编码能力。

首先将所有的边类型组合成一个单一的边类型，从而得到一个同质连通子图。该连通子图实际上是一个包含原始图中完全连通信息的无向图。除了学习直连关系，还引入了一个完全连通子图来学习间接连接节点之间的隐含关系。

每个编码层中的输出z计算如下：

$$\begin{equation}\begin{split} z &= FFN(concat(z^{G^{sub}_1},...,z^{G_M^{sub}})W^O)\\ z_i^{G_m^sub} &= \sum_{j\in N_i^{G^{sub}_m} }\alpha_{ij}(x_jW^V), m\in[1,M] \end{split}\end{equation}$$

$W^O\in R^{Md_z\times d_z}$参数矩阵

作者还采用了子层之间的残差连接、FFN以及层归一化。

Layer Aggregation

编码层之间更好的信息传播可能带来更好的性能。

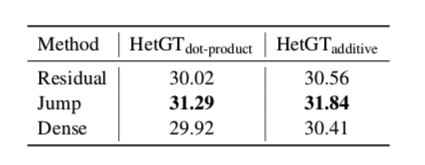
因此，我们研究了三种不同的Layer Aggregation方法，如图3所示。

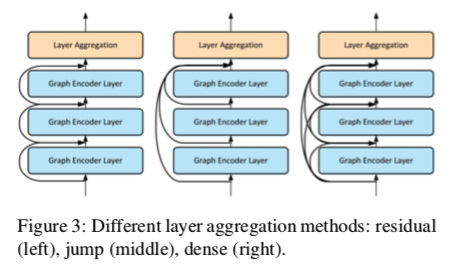
当更新第 $l$ 层节点的表示时，最近的方法是先聚合邻居，然后将聚合结果与来自 $(l−1)$ 层的节点表示相结合。此策略可视为不同图层之间跳过连接的一种形式。

$$\begin{equation}\begin{split} z_{N_i}^{(l)} &= AGGREGATE(\{z_j^{(l-1)}, \forall j \in N_i\})\\ z_i^{(l)} &= COMBINE(z_{N_i}^{(l)}, z_i^{(l-1)}) \end{split}\end{equation}$$

残差连接是另一种著名的跳跃连接，它使用identity mapping作为组合函数来帮助信号传播，但这些跳跃连接不能独立自适应地调整最后一层表示的邻域大小。

如果我们为$z_i^{(l)}$ skip一个层，则所有后续的单元例（如使用此表示的$z_i^{(l+j)}$) 都将隐式的使用此skip

因此，为了有选择地聚合前几层的输出，我们在模型中引入了跳跃体系。

在编码器的最后一层L，通过concat的方式组合前几个编码层的所有输出，以帮助模型有选择地聚合所有这些中间表示。

$$z_i^{final} = Concat(z_i^{(L)},...,z_i^{(1)},x_i) W_{jump}$$

$W_{jump}\in R^{(Ld_z+d_x)\times d_z}$

此外，为了更好地改善信息传播，还可以引入稠密连通性。通过密集连接，l层中的节点不仅从第(l−1)层获取输入，而且还从所有前面的层提取信息：

$$z_i^{(l)} = Concat(z_i^{(l-1)},..,z_i^{(1)},x_i) W^{(l)}_{dense}$$

$W^{(l)}_{dense} \in R^{d^{(l)}\times d_z}, d^{(l)}=d_x+d_z\times(l-1)$