A Generalization of Transformer Networks to Graphs

作者提出了一种适用于任意图的Transformer结构的。

针对问题:

最初的Transformer相当于一个在所有单词之间都有连接的全连通图上操作，但这样的体系结构没有利用图的连通感应偏差，并且当图拓扑结构重要时，没有被编码到节点特征汇总，性能不好。

解决方案

作者提出四个新特性：

首先，注意机制是图中每个节点的邻域连通性的函数。
其次，位置编码由Laplacian特征向量来表示，用在了原始Transformer在NLP中常用的正弦位置编码。
第三，用batch normalization层代替layer normalization，提供了更快的训练速度和更好的泛化性能。
最后，将对任务至关重要的边缘特征表示，加入到该graph-transformer结构中。

方法

图的稀疏性

在NLP Transformer中，句子被视为完全连通的图形，这种选择有两个原因：

很难在句子中的单词之间找到有意义的稀疏交互或联系。例如，句子中的一个词对另一个词的依赖性可以随上下文、用户的视角和特定应用而变化。一个句子中的词之间可能存在许多似是而非的基本事实连接，因此，句子的文本数据集没有显式的词交互可用。因此，让一个句子中的每个单词相互关注其他单词是有意义的，就像Transformer架构所遵循的那样。
在NLP Transformer中考虑的所谓的图通常具有少于数十或数百个节点。这在计算上是可行的，大型变压器模型可以在这种完全连通的文字图上进行训练。

在高达数百万或数十亿的节点大小。可用的结构为我们提供了丰富的信息源，可以作为神经网络中的归纳偏差加以利用，而节点大小实际上使得这样的数据集不可能有一个完全连通的图。

图的位置编码

在NLP中，大多数情况下，基于Transformer的模型由每个字的位置编码补充。这对于确保每个单词的唯一表示以及甚至保留距离信息是至关重要的。

对于图，唯一节点位置的设计是具有挑战性的，因为存在防止规范节点位置信息的对称 。事实上，大多数GNN学习的是节点位置不变的structural node信息。

这就是为什么简单的基于注意力的模型，如GAT，其中attention是局部邻域连通性的函数，而不是全图连通性。

为了更好地对距离感知信息进行编码，(附近节点具有相似的位置特征，而较远的节点具有不同的位置特征)使用拉普拉斯特征向量作为图变换中的PE。

作者在训练过程中随机反转特征向量的符号，遵循 Benchmarking graph neural networks 的做法。预先计算了数据集中所有图的拉普拉斯特征向量。通过对图的拉普拉斯矩阵进行因式分解来定义特征向量；

$\Delta = I - D^{-1/2}AD^{-1/2}=U^T\Lambda U$

使用节点的k个最小特征向量作为其位置编码，并对节点 $i$用 $λ_i$表示。

Graph Transformer Architecture

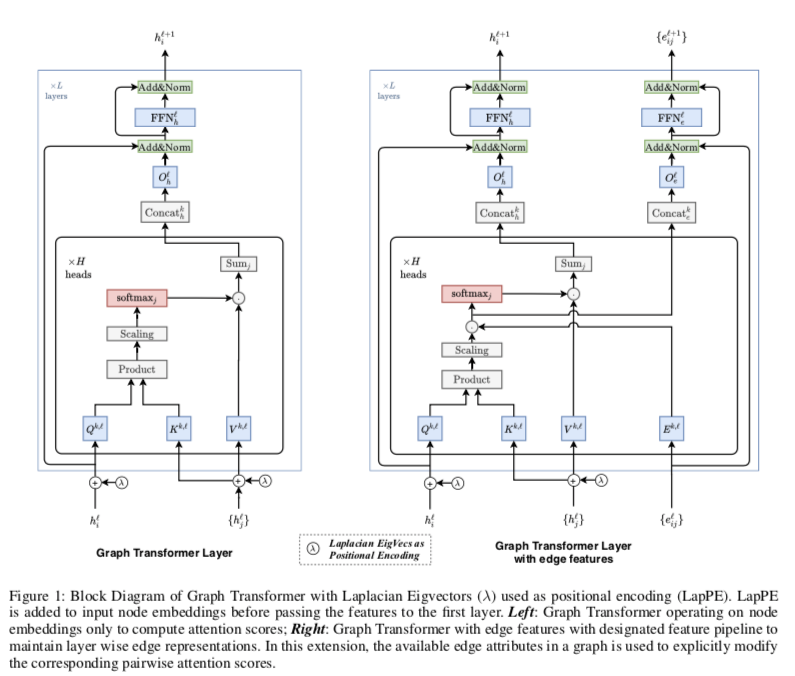
左边的模型是为没有明确边属性的图设计的，右边的模型维护一个指定的边特征，以结合可用的边信息并在每一层维护它们的抽象表示。

输入

图 $G$ 的节点特征 $\alphai \in R^{d_n \times 1}$ ，节点$i,j$ 对应的边特征$\beta{ij}\in R^{d_e \times 1}$

$\alphai, \beta{ij}$ 通过线性映射成为$d$ 维隐层特征 $hi^0 , e{ij}^0$ :

$\hat h_i^0 = A^0\alpha_i + a^0 ; e_{ij}^0 = B^0\beta_{ij}+b^0$

其中，$A^0\in R^{d\times d_n}, B^0\in R^{d\times d_e}, a,b\in R^d$

将位置编码线性映射后加入节点特征:

$\lambda_i^0 = C^0\lambda_i +c^0; h_i^0 = \hat h_i^0 + \lambda_i^0$

其中，$C^0\in R^{d\times k}, c^0 \in R^d$ . 请注意，拉普拉斯位置编码仅添加到输入层的节点特征，而不是在中间层。

Graph Transformer Layer

第 $l$ 层节点更新:

$\begin{equation}\begin{split} \hat h_i^{l+1} &= O^l_h \parallel_{k=1}^H \left ( \sum_{j\in N_i} w_{ij}^{k,l} V^{k,l} h^l_j \right )\\ where, w_{i,j}^{k,l} &= softmax_j(\frac{Q^{k,l} \cdot K^{k,l}h_j^l}{\sqrt{d_k}}) \end{split}\end{equation}$

其中，$Q^{k,l}, K^{k,l}, V^{k,l} \in R^{d_k \times d}, O^{l}_h\in R^{d\times d}$ ，$k$ 注意力haed数。

为了数值稳定性，在取softmax 的输出被限制介于−5到+5之间。

然后，将attention输出$h^{l+1}$传递给FFN，然后是残差和归一化层，如下所示：

$\begin{equation}\begin{split} \hat{\hat {h}}_i ^{l+1} &= Norm(h_i^l + \hat h^{l+1}_i) \\ \hat{\hat{\hat{h_i}}}^{l+1} &= W_2^l ReLU(W_1^l \hat{\hat {h}}_i ^{l+1}) \\ h^{l+1}_i &= Norm(\hat{\hat {h}}_i ^{l+1}+\hat{\hat{\hat{h_i}}}^{l+1}) \end{split}\end{equation}$

其中 $W_1^l\in R^{2d \times d}, W_2^l \in R^{d\times 2d}$ 为了说明清楚，省略了偏执项。

Graph Transformer Layer with edge features

旨在更好地利用图数据集中以边属性形式提供的丰富特征信息。

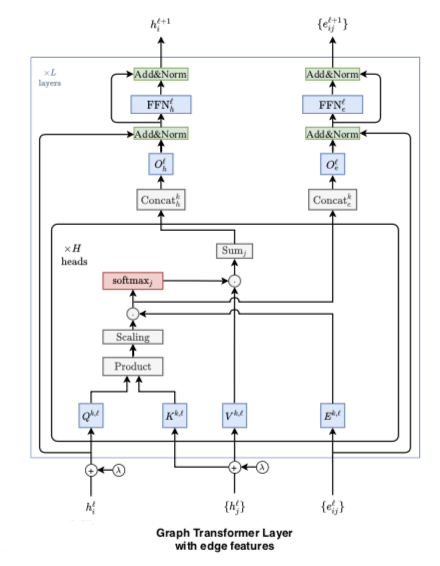
这些边特征是对应于节点对的相关分数，所以将这些可用的边特征与通过 pairwise attention计算的隐含边分数联系起来。换言之，假设在query 和 key 特征投影相乘之后，当节点 $i$ 关注节点 $j$ 时，计算在softmax注意分数 $\hat w{ij}$，将该分数 $\hat w{ij}$ 视为关于边 $$的隐含信息。

利用边特征改进已经计算的隐式注意分数 $\hat w{ij}$ 。通过简单地将两个值 $\hat w{ij}$ 和 $e_{ij}$ 相乘来实现的

指定的节点对称的边特征表示管道，用于将边属性从一层传播到另一层：

$\begin{equation}\begin{split} \hat h_i^{l+1} &= O^l_h \parallel_{k=1}^H \left ( \sum_{j\in N_i} w_{ij}^{k,l} V^{k,l} h^l_j \right )\\ \\ \hat e^{l+1}_{ij} &= O^l_e \parallel_{k=1}^H(\hat w_{ij}^{k,l}),\\ \\ where, w_{ij}^{k,l} &= softmax_j(\hat w_{ij}^{k,l}) ,\\ \\ \hat w_{ij}^{k,l} &= \left(\frac{Q^{k,l} \cdot K^{k,l}h_j^l}{\sqrt{d_k}} \cdot E^{k,l}e^{l}_{ij} \right) \end{split}\end{equation}$

其中 $Q^{k,l}, K^{k,l}, V^{k,l} ,E^{k,l} \in R^{d_k\times d} , O^l_h,O^l_e\in R^{d\times d}$

其余d 也是要经过Transformer架构中的其他成分。