旋转数组的最小数字&搜索旋转排序数组

旋转数组最小数字

题目

把一个数组最开始的若干个元素搬到数组的末尾，我们称之为数组的旋转。

输入一个升序的数组的一个旋转，输出旋转数组的最小元素。

例如数组 {3,4,5,1,2}{3,4,5,1,2} 为 {1,2,3,4,5}{1,2,3,4,5} 的一个旋转，该数组的最小值为 11。

数组可能包含重复项。

注意：数组内所含元素非负，若数组大小为 00，请返回 −1−1。

样例

1
2
3
输入：nums = [2, 2, 2, 0, 1]

输出：0

解法：二分查找

题目中有排序两字，自然较优的解是涉及到二分法的

假设我们用下图表示数组，水平线代表数字相同，横坐标代表数字下标

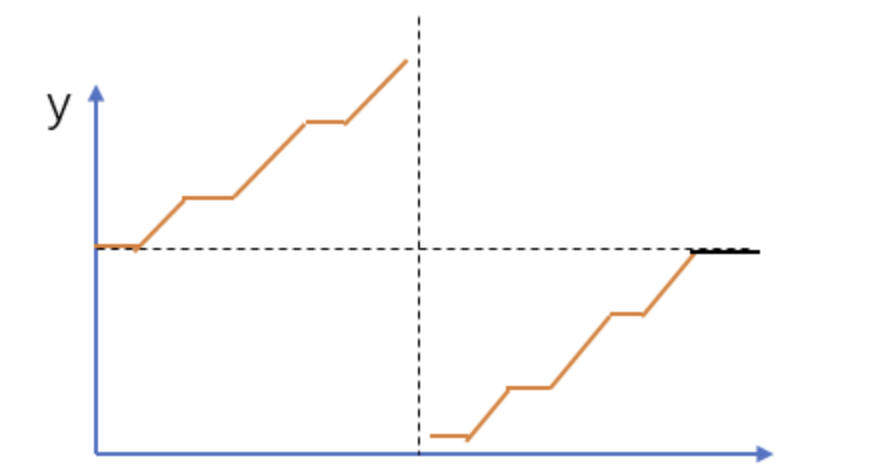
我们发现除了最后水平的一段（黑色水平那段）之外，其余部分满足二分性质：

竖直虚线左边的数满足 $numbers[i] ≥ numbers[0]$ ；

而竖直虚线右边的数不满足这个条件。

我们要找的便是不满足上诉性质的那段中的最小值。

所以我们先将最后水平的一段删除 , 使得右半段不满足 $numbers[i] ≥ numbers[0]$ ，而是严格满足 $numbers[i] < numbers[0]$。

另外，如果处理数组完全单调的情况：

当删除最后一段后，如果剩下的最后一个大于等一第一个数，说明数组完全单调。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
    public int findMin(int[] numbers) {
        if(numbers == null || numbers.length==0) return -1;
        int left=0;
        int right = numbers.length-1;
        // 去除第二段有序数组中最后的和第一段第一个数相同的数
        // 使得第二段有序数组严格满足numbers[i]<numbers[0]
        while(right>0 && numbers[right]==numbers[0]){
            right--;
        }
        // 如果此时整个数组都有序了，那么numbers[0]就是最小值
        if(numbers[0] < numbers[right]){
            return numbers[0];
        }
        
        while(left<right){
            int mid = left+right>>1;
            if(numbers[mid] < numbers[0]){ // 说明mid落在了右半段，最小值在[left,mid]里
                right = mid;
            }else{
                left = mid +1;
            }
        }
        return numbers[left];
    }
}

搜索旋转数组

数组旋转后可画出如下图：

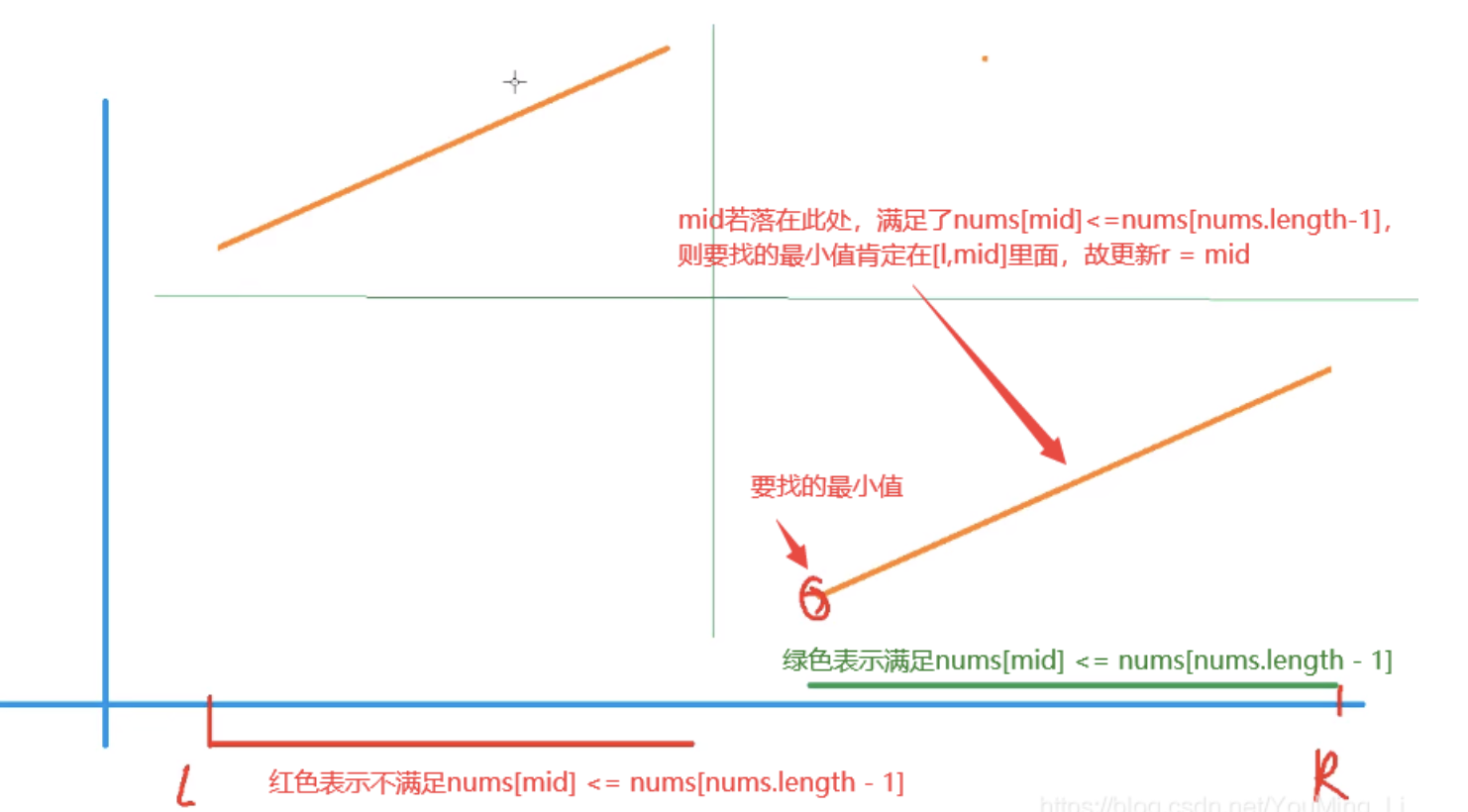
橙色线表示的就是旋转后数组的左右两个部分。不难发现，如果下标落在右半部分，则一定有 $nums[mid] <= nums[nums.length-1]$

判断 $nums[mid] <= nums[nums.length-1]$ 是否成立

  • 成立：说明当前mid落在了数组的右半部分，而我们要找的最小值其实就是右半部分的开头，故更新区间为 $[l,mid]$ 。
  • 否则：说明mid落在了旋转数组的左半部分，那么右半部分的起点则在 $[mid+1, r]$

总之，要找满足 $nums[mid] <= nums[nums.length-1]$ 的最小值

第二阶段

找到最小值后，假如最小值的下标是 min ，数组便可以分为有序的两半 $[l, min-1]$ 和 $[min, r]$ 此时判断 $target<=nums[nums.length-1]$ 。

若成立，可以再右半部分中找target，因为target如果在右半部分的话，一定大于 $nums[nums.length-1]$， 那么久应该去左半边 $[l, min-1]$ 中找 target

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
class Solution {
    public int search(int[] nums, int target) {
        if(nums==null || nums.length==0) return -1;
        //1,找出数组中的最小值,即左右两边的分界点，便可以将数组分为有序的左右两边
        //2,判断target <= nums[nums.length - 1]是否成立
        //  成立：target在旋转后的右半边
        //  不成立：target在旋转数组的左半边
        int l =0 ;
        int r = nums.length-1;
        while(r>0 && nums[r]==nums[0]){
            r--;
        }

        while(l<r){
            int mid = l+r >>1;
            if(nums[mid] <= nums[nums.length-1]){
                r=mid;
            }else{
                l=mid+1;
            }
        }
        //上面while结束后，l = r，都指向旋转数组中的最小值
        if(target<=nums[nums.length-1]){
            // target在右边， l本身就是指向右边起点的，不用更新，更新r为右边终点。
            r = nums.length-1;
        }else{
            //target在左半边
            l = 0;//左半边的起点
            r--;//让r指向最小值的前一个位置，即左半边的终点
        }
        //定好了区间[l,r]后，可以在里面找target了
        //使用二分模板即可，找满足nums[mid] >= target的最小值
        while(l<r){
            int mid = l+r>>1;
            if(nums[mid] >= target){
                r=mid;
            }else{
                l=mid+1;
            }
        }
        // 判断最终找到的num[l]是否等于target
        if(nums[l] == target) return l;
        return -1;


    }
}